介紹了一種分析同軸線變換器的新方法，建立了理想與通用模型，降低了分析難度和簡化了分析過程。通過研究分析，提出了一種同軸變換器與集總元件相結(jié)合的匹配電路設(shè)計(jì)方法，通過優(yōu)化同軸線和集總元件的參數(shù)，實(shí)現(xiàn)放大器的最佳性能。利用該方法設(shè)計(jì)了一款應(yīng)用于推挽式功率放大電路的匹配電路，仿真結(jié)果表明，匹配效率高達(dá)99.93%。

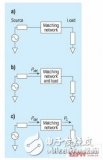
阻抗變換器和阻抗匹配網(wǎng)絡(luò)已經(jīng)成為射頻電路以及最大功率傳輸系統(tǒng)中的基本部件。為了使寬帶射頻功率放大器的輸入、輸出達(dá)到最佳的功率匹配，匹配電路的設(shè)計(jì)成為射頻功率放大器的重要任務(wù)。要實(shí)現(xiàn)寬帶內(nèi)的最大功率傳輸，匹配電路設(shè)計(jì)非常困難。本文設(shè)計(jì)的同軸變換器電路就能實(shí)現(xiàn)高效率的電路匹配。同軸變換器具有功率容量大、頻帶寬和屏蔽好的特性，廣泛應(yīng)用于VHF/UHF波段。常見的同軸變換器有1:4和1:9阻抗變換，如圖1所示。但是實(shí)際應(yīng)用中，線阻抗與負(fù)載不匹配時(shí)，它們的阻抗變換不再簡單看作1:4或1:9.本文通過建立模型，提出一種簡化分析方法。

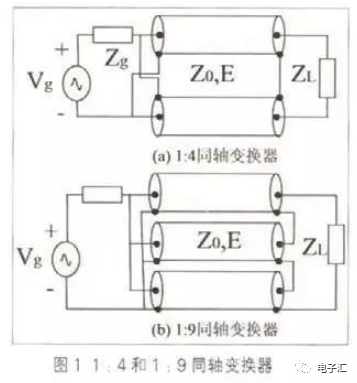
1 同軸變換器模型

同軸變換器有三個(gè)重要參數(shù)：阻抗變換比、特征阻抗和電長度。這里用電長度是為了分析方便。當(dāng)同軸線的介質(zhì)和長度一定時(shí)，電長度就是頻率的函數(shù)，可以不必考慮頻率。

1.1理想模型

理想的1:4變換器的輸入、輸出阻抗都匹配，每根同軸線的輸入、輸出阻抗等于其特征阻抗Z0,其等效模型如圖2所示。

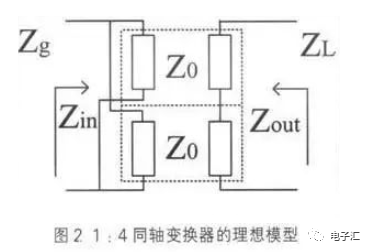
其源阻抗Zg與ZL負(fù)載阻抗變換比為：

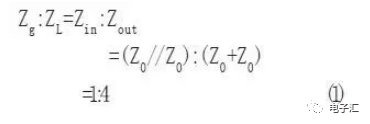
圖2和公式（1）表明：變換器的阻抗變換比等于輸入阻抗與輸出阻抗之比。

同軸變換器的輸入阻抗等于同軸線的輸入阻抗并聯(lián)，輸出阻抗等于同軸線的輸出阻抗串聯(lián)。

1.2通用模型

由于特征阻抗是實(shí)數(shù)，而源阻抗與負(fù)載阻抗一般都是復(fù)數(shù)，所以，就不能簡單的用變換比來計(jì)算。阻抗匹配就是輸入阻抗等于源阻抗的共軛，實(shí)現(xiàn)功率的最大傳輸。特征阻抗為Z0,電長度為E的無耗同軸線接復(fù)阻抗的電路如圖3所示。

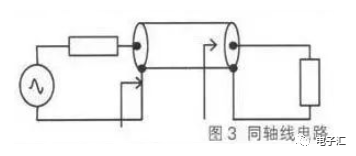
由于源阻抗與同軸線特征不匹配，電路的反射系數(shù)就不是負(fù)載反射系數(shù)。

由于同軸線是無耗的，進(jìn)入同軸線的功率就等于負(fù)載消耗的功率。那就可以把電路簡化只有一個(gè)負(fù)載Zin,又因?yàn)閆g與Zin都是復(fù)數(shù)且串聯(lián)，就可以把Zg中的虛部等效到Zin中，最后得到反射系數(shù)為：
?

其中：

當(dāng)反射系數(shù)為零時(shí)，功率可以無反射的傳輸，這時(shí)阻抗實(shí)現(xiàn)完全匹配。

由公式（2），反射系數(shù)為零可以等效為分子為零，即：

其中：
?

當(dāng)E為90o時(shí)，可得：

由于特征阻抗為實(shí)數(shù)，ZLZg*為實(shí)數(shù)時(shí)，方程才有解或才能完全匹配。當(dāng)ZL和Zg為實(shí)數(shù)時(shí)，就是常用的λ/4阻抗變換。

當(dāng)E不等于900,利用實(shí)部與虛部都等于零得方程組：

整理化簡得：

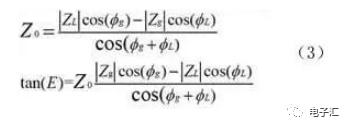
公式（3）說明，不是任意兩個(gè)復(fù)阻抗都可以完全匹配，必須滿足特征阻抗為正實(shí)數(shù)；可以并聯(lián)或串聯(lián)電抗元件，使兩個(gè)不可能完全匹配的復(fù)阻抗完全匹配。

通用模型是結(jié)合理想模型和同軸線分析建立，如圖4所示。把1:N同軸變換器等效一根同軸線，利用同軸線的分析結(jié)果，更容易獲得特征阻抗和電長度參數(shù)。

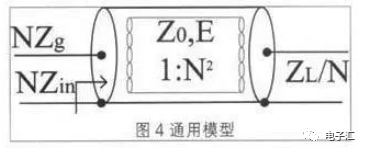
特別對于利用同軸變換器設(shè)計(jì)的匹配電路，可以簡化設(shè)計(jì)步驟，減少工作量。

2 寬帶匹配電路的設(shè)計(jì)

通過對同軸變換器的分析，可以通過調(diào)諧特征阻抗和電長度完成阻抗匹配。

但是實(shí)際同軸線的特征阻抗是有一定規(guī)格的，不是任意的，而且電長度又是隨頻率變化的，所以采用同軸變換器和集總元件聯(lián)合實(shí)現(xiàn)寬帶匹配的方式。

2.1.集總元件匹配電路

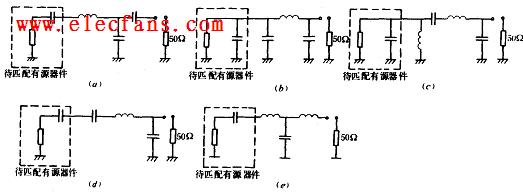
復(fù)阻抗可以用電阻與電抗串聯(lián)表示，也可以用電阻與電抗并聯(lián)表示，這兩種表示的等效電路如圖5所示。

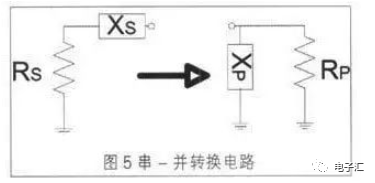
它們都是指同一個(gè)復(fù)數(shù)，其轉(zhuǎn)換關(guān)系為：

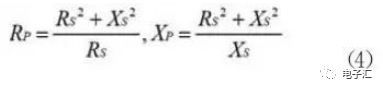
公式4表明，電阻并聯(lián)電抗可以減小其復(fù)阻抗的實(shí)部，再串聯(lián)電抗抵消其虛部，就可以實(shí)現(xiàn)Rp到RS阻抗匹配。所需的電抗值可以通過表達(dá)式4計(jì)算，且Xp與XS取不同性質(zhì)的元件，如果Xp用電容，XS就用電感。

集總元件實(shí)現(xiàn)阻抗匹配原理：電阻并聯(lián)電抗減小其實(shí)部，再串聯(lián)電抗抵消其虛部，達(dá)到兩個(gè)純電路的匹配；當(dāng)匹配的不是純電阻時(shí)，可以采用抵消和吸納虛部的方法實(shí)現(xiàn)復(fù)阻抗的匹配。

2.2聯(lián)合匹配電路

以Freescale公司MRF6VP2600推挽式MOSFET管的匹配電路設(shè)計(jì)為例，首先確定匹配電路的基本結(jié)構(gòu)和同軸變換器的阻抗變換，然后再確定特征阻抗、電長度和集總參數(shù)。由于輸入匹配電路設(shè)計(jì)與輸出匹配電路類似，下面詳細(xì)研究輸出匹配電路設(shè)計(jì)。MRF6VP2600的DATASHEET給的源極-源極的輸出阻抗如圖6所示。

圖6 MRF6VP2600的輸入-輸出阻抗

輸出匹配電路中，由于功率管采用推挽式工作，所以在輸出端加入1:1巴倫實(shí)現(xiàn)不平衡-平衡變換。利用通用模型，下面的工作就簡化為同軸線與集總參數(shù)的匹配電路設(shè)計(jì)。同軸線的特征阻抗和電長度計(jì)算公式為：

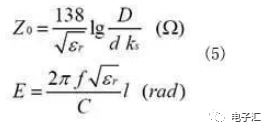
式中，Er為內(nèi)部填充介質(zhì)的相對介電常數(shù)；D為外導(dǎo)體內(nèi)徑；d是內(nèi)導(dǎo)體外徑；為內(nèi)導(dǎo)體系數(shù)，單股內(nèi)導(dǎo)體時(shí)為1;C為空氣中光的速度；f為工作頻率，L為同軸線的長度。

公式5表明，電長度與頻率呈線性關(guān)系，且其長度越短，電長度受頻率的影響越小。

2.3仿真驗(yàn)證

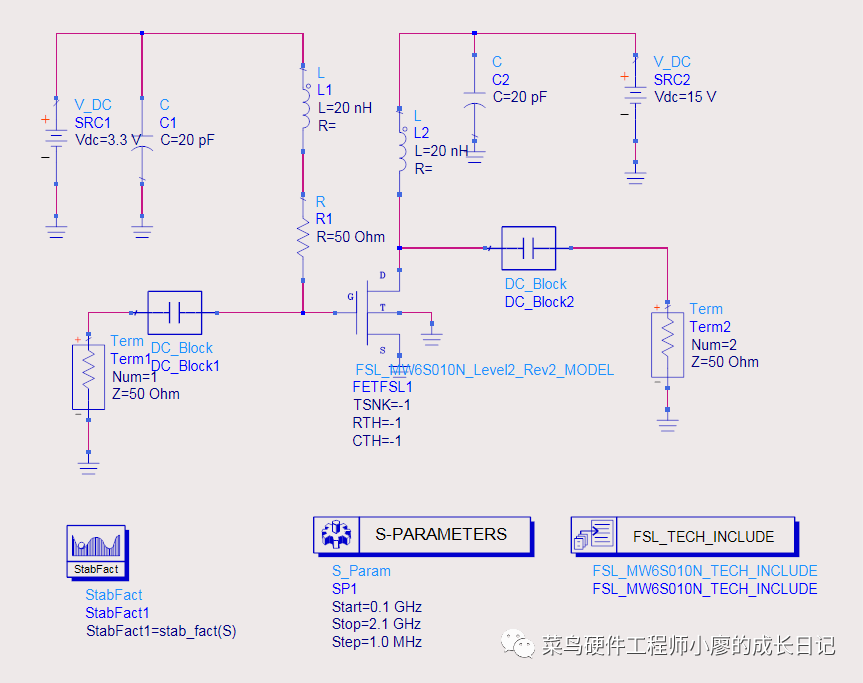
利用安捷倫公司的ADS工具進(jìn)行輸出匹配電路設(shè)計(jì)與仿真，一般可采用大信號S參數(shù)仿真和諧波仿真，由于本文設(shè)計(jì)用于推挽式工作的匹配電路，所以選用更直觀的諧波平衡仿真。利用同軸線和巴倫的模型進(jìn)行仿真的電路如圖7所示。

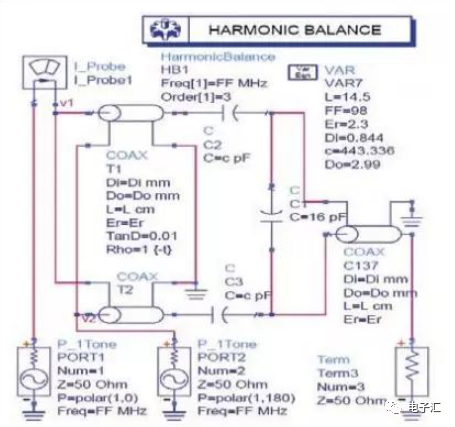
圖7 仿真原理圖

由于圖7的負(fù)載阻抗的實(shí)部是隨頻率增減而減少，所以在同軸變換器的兩端并聯(lián)電容。可以很容易對電路進(jìn)行手動(dòng)調(diào)諧和自動(dòng)優(yōu)化，最后的仿真結(jié)果如圖8所示。

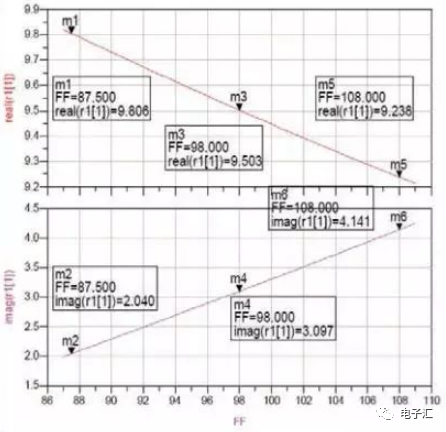
圖8 （87.5-108）Mhz匹配阻抗

由圖6,圖8可以得到各頻點(diǎn)的反射系數(shù)；再根據(jù)反射系數(shù)與頻率的關(guān)系，可以求得匹配電路在工作頻帶的反射系數(shù)；最后根據(jù)匹配效率與反射系數(shù)的關(guān)系，求得匹配電路的匹配效率。具體結(jié)果見表1。

表1 反射系數(shù)與匹配效率的計(jì)算結(jié)果

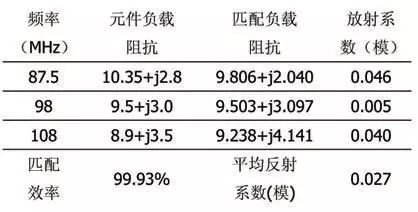
從表1可以得到，匹配電路的在工作頻段內(nèi)匹配效率達(dá)99.93%,實(shí)現(xiàn)了較好的匹配。

3總結(jié)

本文建立同軸變換器的理想模型和通用模型，提出一種新穎的和簡單的分析方法。通過分析，同軸線的特征阻抗和電長度對匹配電路的性能有很大影響。設(shè)計(jì)了一款推挽式MOSFET管的輸出匹配電路，仿真結(jié)果表明：匹配效率達(dá)99.93%.

編輯：黃飛

?