關鍵詞:符號同步 定時錯誤檢測 插值 窗函數
在數字通信系統中,為了限制被傳輸的數字信號的頻譜,需要對其進行滾降升余弦濾波,形成基帶波形,并對載波進行調制,以實現頻帶傳輸。在接收端,需要對經過相干解調、匹配濾波形進行重新采樣得到相應的數字信號。根據奈奎斯特抽樣值無失真準則,A/D轉換器若在最佳采樣時刻進行采樣,得到的采樣值恰好是發送端所要傳遞的數據。但在實際情況下,由于信道傳輸延時以及收發兩地時鐘偏移,使采樣無法在最佳時刻進行,這樣采集到的數據與正確的數據之間存在著偏差,需要有同步措施來調整采樣時鐘或對采樣值進行插修正。

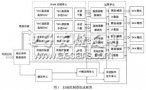
圖1
目前數字接收機中的符號同步大多采用自同步法。其主要有兩種,一種是由定時錯誤檢測(TED)算法加環路濾波器估算采樣時鐘和最佳采樣時刻之間的相位差,然后通過數控振蕩器NCO調整采樣時鐘,稱為同步采樣恢復;另一種也使用相同的方法估算時鐘相差,但它并不調整采樣時鐘相位,而是通過插值算法對采樣值進行修正,稱為異步采樣恢復。由于后者不需要改變時鐘相位,因此具有更好的穩定性,故得到廣泛的應用。 本文提出了一種基于插值算法符號同步的硬件設計方案。在時鐘相差估算環節采用了NDA-ELD算法進行定時錯誤檢測;插值濾波器的設計則采用了理想插值算法加窗處理,與拉格朗日插值濾波器相比,具有更好的頻域特性。該同步方案屬于非數據輔助的同步法。這里所謂的同步,是對采樣值進行插值修正,而不需要對時鐘本身進行相位調整。因此它較適用于對系統時鐘穩定性要求較高的場合,如全數字接收機等。
異步采樣恢復的符號同步設計結構如圖1所示。該方法的關鍵在于插值算法的準確性。針對這一點,本文提出了一種符號同步的硬件設計方案,其插值濾波器的設計采用了理想插值算法加窗處理,與目前所采用的另一種拉格朗日插值濾波器相比,具有更好的頻域特性。
1 時鐘相差的估算
對于最佳采樣時刻和采樣時鐘相位差的估算,本文采用定時錯誤檢測(TED)加環路濾波器實現。其中定時錯誤檢測環節采用NDA-ELD算法,該算法是由最大似然估計法所推導的,它要求A/D轉換器以兩倍的符號頻率對輸入波形進行采樣。公式如下

這里T是符號周期,Ts是采樣間隔,Ts=T/2。e(k)表示采到第k個符號時所得到的定時誤差信息。εк表示采到第k個符號時所估算出的最佳采樣時刻和采樣時鐘之間的相位差,其范圍是[-1,1],即時鐘偏差最多可為1個采樣間隔。y(kTs+εкTs)則是根據εк而對匹配濾波器的輸出y(kTs)進行的差值修正。將e(k)通過一環路濾波器和相位溢出控制器便可得到εк+1,從而實現PID控制。相位溢出控制器主要是對εк+1進行限幅,將其控制在[-1,1]之內。由此可得到時鐘相差估算的設計結構,如圖2。
該算法對于一些幅度或相位調制的信號,如MQAM、BPSK、QPSK等,具有較好的同步性能。在開啟時,它能自動跟蹤開啟的最大處,即最佳采樣時刻。當存在噪聲干擾時,可通過環路濾波器將其濾除,使之對時鐘相差估算產生較小的影響。環路濾波器系數K1、K2的選擇要視具體情況而定,取得過大,同步時間較短,但抖動方差較大;反之,則需要較長的同步時間。本設計是對64QAM信號進行符號同步,經過Matlab的仿真測試,結果表明K1、K2分別取1/512、1/256較為合適。

2 采樣值插值修正
通過以上處理環節可估算出采樣時鐘和最佳采樣時刻之間的相位差,在插值修正環節就可根據該相差進行采樣值修正處理。由內插公式可知,如果采用理想插值,理論上可根據采樣值得到任意時刻的信號值,即:

但理想插值濾波器需要無窮個信號采樣值,這在實際應用中是無法實現的。一般情況下可對理想插值濾波器加窗處理,將其截短。
窗函數的選擇要視具體情況而定。最簡單的窗函數是矩形窗,即對理想插值濾波器直接截短。其優點是設計簡單,具有較窄的過渡帶,且對理想插值濾波器頻率響應具有最好的均方逼近。但它對無限長理想沖激響應直接截取,因此存在著較為明顯的吉布斯現象。此外,其最小阻帶衰減為21dB,這在實際應用中也是不夠的。因此直接截取方式在現實中很少采用。對理想沖激響應進行窗處理的一個較成功的辦法是將窗函數的兩端平滑地減小至零,以減小旁瓣高度,減輕吉布斯現象[4]。在這一思想下,目前常用的窗函數有Han ning、Hamming、Blackman、Kaiser等。本設計采用了Kaiser窗,它是一種近似最佳的窗函數。經過Matlab仿真測試,將Kaiser窗長度定為10Ts,形狀參數β取為2.5248(對應的阻帶最小衰減為33dB),可得到較小的插值平均誤差。由此得到如下公式:

這里h(t)為插值濾波器的沖激響應,它是理想內插函數的Kaiser窗載短形式,長度為10Ts。即:

這里I0(·)表示第一類零階修正Bessel函數。由此可得到其頻率響應H(ω),它是所需理想頻率響應與窗函數傅里葉變換卷積所得。H(ω)對數幅度特性如圖3所示(取Ts=1)。
可見,Kaiser窗函數插值濾波器具有較好的頻域特性。在通帶,它能將衰減穩定在0dB;在阻帶,最小衰減為33dB,且迅速增大。這些均優于目前所用的另一種拉格朗日插值濾波器,其頻譜特性見文獻[4]。利用該濾波器便可對采樣值進行插值修正。由公式(3)可得到如圖4所示的設計結構。
為了使硬件更容易實現,可將εn離散化,即將其取值空間定為{-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1},以取代其在[-1,1]上的連續取值。圖4中,h'(εn+m)=h(εnTs+mTs),其值取決于εn控制9選1選擇器,根據不同的εn輸出不同的
h'(εn+m)的各自取值空間,即理想插值濾波器系數與對應的窗函數值相乘的結果。該結構中應用了移位寄存器,主要是為了避免εn改變時,所造成的算法誤差。這樣在輸入一個y(kTs)后,經過4個采樣周期的延遲,就可得到相應的輸出y(kTs+εnTs),從而完成插值修正。

圖4
文中提到的設計已用VerilogHDL實現,并用Design Compiler對其進行了門級綜合,并用VCS進行了時序驗證,所用的工藝為0.25μm。設計門數約8000門,采樣時鐘可達17.5MHz,平均插值誤差11%左右。
 電子發燒友App
電子發燒友App





















評論