配電網(wǎng)絡(luò)重構(gòu)的改進(jìn)混合遺傳算法

本文提出一種基于改進(jìn)的混合遺傳算法的配電網(wǎng)重構(gòu)算法，在算法中使用可操作開(kāi)關(guān)支路的整數(shù)編號(hào)的排列順序來(lái)表示染色體，并通過(guò)譯碼器的設(shè)計(jì)來(lái)映射染色體所對(duì)應(yīng)的輻射狀網(wǎng)絡(luò)結(jié)構(gòu)，避免了產(chǎn)生不可行解的情況，大大提高了算法的運(yùn)算效率。同時(shí)在算法中引入了局部尋優(yōu)算子，改善了算法的局部尋優(yōu)性能。算例結(jié)果表明本算法是高效，可行的。
　　關(guān)健字 網(wǎng)絡(luò)重構(gòu)；遺傳算法；局部尋優(yōu)算法

A refined hybrid genetic algorithm for
distribution network reconfiguration

ZHENG Xin1，YANG Li-xi1，C.T.Tse2

(1.College of Electrical Engineering，ZhengZhou University，
ZhengZhou，450002，China；
2.The Hong Kong Polytechnic University，Electric Engineering?
Department，China)

　　Abstract: This paper proposes an improved solution for distribution network reconfiguration based on a refined hybrid genetic algorithm. In the algorithm the "the integer permutation" encoding is adopted with each integer representing one controllable switch. A decoder is designed to decide the final network configuration corresponding every chromosome. A local search operator is combined with the genetic algorithm which improve the local optimal capability of the algorithm. The computational result on a tested system demonstrate the algorithm is feasible and efficient.?
　　Key words: Network reconfiguration；Hybrid genetic algorithm；Local search algorithm；

1 引言
　　基于網(wǎng)損最小的配網(wǎng)重構(gòu)問(wèn)題是一個(gè)典型的非線(xiàn)性、多約束的整數(shù)組合優(yōu)化問(wèn)題，配電網(wǎng)的輻射狀結(jié)構(gòu)和弱環(huán)網(wǎng)特性是其重構(gòu)的前提條件。基于圖論，配電網(wǎng)的結(jié)構(gòu)可以用圖G(N,B)描述，N表示電源節(jié)點(diǎn)和負(fù)荷節(jié)點(diǎn)的集合，B表示饋線(xiàn)段集合，配網(wǎng)的輻射狀結(jié)構(gòu)就由圖的多個(gè)樹(shù)來(lái)組成，T={t1t2t3t4...tn,l1l2...lm}，其中樹(shù)支t為供電支路，連支l為聯(lián)絡(luò)支路。這樣，配網(wǎng)重構(gòu)問(wèn)題，可以被描述為在圖中尋找一個(gè)使得總網(wǎng)損最小并滿(mǎn)足運(yùn)行約束的樹(shù)狀結(jié)構(gòu)。一個(gè)大型的配網(wǎng)包含眾多的節(jié)點(diǎn)和支路，因此圖中支撐樹(shù)的組合數(shù)目極大，若窮舉所有的樹(shù)，算法將非常的低效。
　　遺傳算法具有全局收斂性、無(wú)可微性要求、具有很好的魯棒性等優(yōu)點(diǎn)，特別適合于求解組合優(yōu)化問(wèn)題。另外，與一般的隨機(jī)搜索方法進(jìn)行的盲目無(wú)向搜索不同，遺傳算法進(jìn)行的是高效有向的全局搜索，能夠逐步地逼近并收斂于全局最優(yōu)解。因此，遺傳算法在配網(wǎng)重構(gòu)中得到越來(lái)越廣泛的應(yīng)用。
　　但是，遺傳算法對(duì)于求解配網(wǎng)重構(gòu)這樣的非線(xiàn)性組合優(yōu)化問(wèn)題，還存在兩個(gè)重要的缺陷，一是父代的優(yōu)質(zhì)基因結(jié)構(gòu)對(duì)于子代影響甚小，采用常規(guī)遺傳算法，收斂速度相當(dāng)慢；二是配網(wǎng)重構(gòu)是一個(gè)強(qiáng)約束的問(wèn)題，對(duì)于電流、電壓等約束，可以用懲罰因子來(lái)進(jìn)行約束，但對(duì)于出現(xiàn)環(huán)網(wǎng)和孤島的組合無(wú)法用一個(gè)合適的評(píng)價(jià)函數(shù)來(lái)進(jìn)行評(píng)價(jià)。文獻(xiàn)[1]-[4]提出了不同編碼、雜交和變異算子設(shè)計(jì)方法雖然在一定程度上提高了算法的效率，但是這些基于二進(jìn)制編碼方法的算法在產(chǎn)生下一代的時(shí)候都不可避免地出現(xiàn)大量的不可行解。在這些文獻(xiàn)中對(duì)于不可行解的處理方法分為兩種，一種是刪除，補(bǔ)充可行解進(jìn)入新生代；另一種方法是修補(bǔ)，將不可行解的網(wǎng)絡(luò)結(jié)構(gòu)通過(guò)打開(kāi)開(kāi)關(guān)解環(huán)，合上開(kāi)關(guān)消除孤島，使不可行解變?yōu)榭尚薪狻＿@兩種方法雖然在理論上是可行的，但只適合于每一代出現(xiàn)很少量的不可行解的情況。在一個(gè)復(fù)雜、多環(huán)的配網(wǎng)中，這些算法在每一代中都將產(chǎn)生大量的不可行解，要耗費(fèi)大量的時(shí)間來(lái)判斷解是否可行，而補(bǔ)充新的可行解與修補(bǔ)不可行解也是非常困難和耗時(shí)的，增加了算法的復(fù)雜度。同時(shí)由于進(jìn)行大量的修補(bǔ)和補(bǔ)充新個(gè)體，子代不能保持與父代的親體相似性，父代中的優(yōu)質(zhì)基因結(jié)構(gòu)在子代中遭到完全破壞，算法最終可能蛻變成盲目的隨機(jī)搜索，收斂速度慢，甚至出現(xiàn)不能收斂的現(xiàn)象，失去了遺傳算法的意義。
　　本文提出一種改進(jìn)的混合遺傳算法，在常規(guī)的遺傳算法中加入局部尋優(yōu)算子來(lái)改善算法的局部尋優(yōu)性能，同時(shí)通過(guò)編碼器和譯碼器相結(jié)合的設(shè)計(jì)方法完全避免了出現(xiàn)不可行解的問(wèn)題，進(jìn)一步提高了遺傳算法的搜索效率，從而加快遺傳算法的收斂速度。

2　配網(wǎng)重構(gòu)的數(shù)學(xué)模型
　　配網(wǎng)重構(gòu)的目的就是在滿(mǎn)足運(yùn)行約束的前提下，使系統(tǒng)的網(wǎng)損達(dá)到最小。因此配網(wǎng)重構(gòu)的目標(biāo)函數(shù)可以表示為：
?
其中:Ie是支路e的電流，Re是支路e的電阻，Ke表示支路的開(kāi)關(guān)狀態(tài)，1表示支路開(kāi)關(guān)處于閉合狀態(tài)，0表示支路開(kāi)關(guān)處于斷開(kāi)狀態(tài)；(2)式代表支路電流過(guò)載約束，Iemax表示支路電流的上限；（3）式代表節(jié)點(diǎn)電壓約束，Vimin、Vimax分別表示節(jié)點(diǎn)的電壓的上下限，（4）式代表輻射狀網(wǎng)絡(luò)且不出現(xiàn)孤島的拓?fù)浼s束。本文通過(guò)前推回代的潮流算法來(lái)求解配網(wǎng)網(wǎng)損，并用約束條件進(jìn)行驗(yàn)證。

3　遺傳算法在網(wǎng)絡(luò)重構(gòu)中的改進(jìn)
3. 1 編碼和譯碼策略
??? 編碼設(shè)計(jì)就是如何用一個(gè)染色體來(lái)表示一個(gè)唯一的配電網(wǎng)網(wǎng)絡(luò)結(jié)構(gòu)；本文將配電網(wǎng)中所有的可操作的開(kāi)關(guān)支路進(jìn)行整數(shù)編號(hào)，染色體是由所有這些支路號(hào)的隨意排列組成，染色體中不允許出現(xiàn)相同的支路號(hào)，染色體的長(zhǎng)度為可操作開(kāi)關(guān)支路的數(shù)目。如一個(gè)16節(jié)點(diǎn)的配電系統(tǒng)，16條支路從1到16進(jìn)行編號(hào)，其中一個(gè)染色體就可以表示為：
??? [1 2 3 5 6 7 8 9 10 12 14 15 16 4 11 13]
??? 對(duì)于遺傳算法而言，僅隨機(jī)產(chǎn)生不同順序的串，為了使串表示一個(gè)有效的網(wǎng)絡(luò)拓?fù)洌@就需借助于譯碼器的實(shí)現(xiàn)。譯碼器的目標(biāo)就是如何根據(jù)染色體的編碼來(lái)構(gòu)造出一個(gè)唯一的支撐樹(shù)。
??? 本文在譯碼器的設(shè)計(jì)中，采取避圈法生成樹(shù)的構(gòu)造方法：圖開(kāi)始時(shí)，只有節(jié)點(diǎn)沒(méi)有邊，樹(shù)支和連支的集合為空，按照染色體中支路號(hào)從左到右的排列順序，選擇支路號(hào)對(duì)應(yīng)的一條邊來(lái)加入圖中；如果與圖中的邊不構(gòu)成環(huán)，就作為樹(shù)支放入樹(shù)支集合中，否則作為連支放入連支集合中，重復(fù)這個(gè)過(guò)程，直到不能進(jìn)行為止；這樣最后將形成樹(shù)的形式，樹(shù)支即為閉合支路，連支為打開(kāi)的聯(lián)絡(luò)支路。可見(jiàn)在避圈法生成樹(shù)的過(guò)程中，在一個(gè)弱環(huán)中先加入的邊會(huì)成為樹(shù)支，而最后加入的邊由于會(huì)形成環(huán)，只能作為連支，所以加入邊的順序不同也就是染色體的不同產(chǎn)生的樹(shù)就有可能不同，同時(shí)通過(guò)這種方法每一個(gè)染色體必然只對(duì)應(yīng)出唯一一個(gè)樹(shù)狀結(jié)構(gòu)的配網(wǎng)。雖然不同的染色體對(duì)應(yīng)的樹(shù)可能是一樣的，如在上面的樹(shù)如果表示為一個(gè)染色體，隨意改變中樹(shù)支的排列順序和隨意改變連支的排列順序根據(jù)避圈法生成的樹(shù)都是一樣的，但是我們可以在產(chǎn)生初始代時(shí)通過(guò)連續(xù)大范圍的交叉轉(zhuǎn)換來(lái)減少出現(xiàn)等價(jià)染色體的機(jī)率。在本文的算例中，通過(guò)特定的交叉和變異方法在每一代中只有很少的機(jī)率出現(xiàn)等價(jià)或相同的染色體。由于這種通過(guò)譯碼器構(gòu)造支撐樹(shù)的方法，對(duì)應(yīng)的很自然的就是可行解，所以就不需要再判斷網(wǎng)絡(luò)結(jié)構(gòu)是否符合網(wǎng)絡(luò)拓?fù)浼s束的問(wèn)題，省去了各種對(duì)不可行解的處理步驟，大大提高了解的質(zhì)量和算法的運(yùn)算效率，加快了解的收斂速度。
3.2 交叉算子設(shè)計(jì)
??? 基于構(gòu)造支撐樹(shù)的順序編碼，若采用簡(jiǎn)單的一點(diǎn)或多點(diǎn)交叉策略，必然以極大的概率產(chǎn)生不可行的染色體，因此本文采用與部分匹配交叉比較類(lèi)似的交叉方法，方法如下：
??? (1)隨機(jī)在串中選擇一個(gè)交配區(qū)域，如兩父串及交配區(qū)域選定為:
??? A=12|3456|789???? B=98|7654|321
??? (2)將B的交配區(qū)域加到A的前面或后面，A的交配區(qū)域加到B前面或后面得到:
??? A′=7654|123456789???? B′=3456|987654321
??? (3)在A′和B′中自交配區(qū)域后依次刪除與交配區(qū)相同的城市碼、得到最終的兩子串為:
??? A″=765412389?? B″=345698721
??? 與其它方法相比，這種方法在兩父類(lèi)相同的情況下仍能產(chǎn)生一定程度的變異效果，這對(duì)維持群體內(nèi)一定的多樣化特性有一定的作用，實(shí)驗(yàn)中也顯示了較好的結(jié)果。
3.3 變異
　　為了維持群體內(nèi)的多樣化，本文采用隨機(jī)連續(xù)多次對(duì)換的變異技術(shù)，使可行解在順序上有了較大的變化，以抑制交叉中有可能產(chǎn)生的同化作用。
　　所謂隨機(jī)對(duì)換變異，就是隨機(jī)選擇串中的兩點(diǎn)，交換其編碼。例如對(duì)于串A:
????? A=12|3456|789
　　如果隨機(jī)產(chǎn)生的交換點(diǎn)是2和7，則串A中的第2點(diǎn)和第7點(diǎn)將對(duì)換，對(duì)換后，串A變?yōu)椋?br>???? A′=17|3456|289
　　由于經(jīng)過(guò)一次對(duì)換后，A′仍然有可能與A表示為同一個(gè)網(wǎng)絡(luò)結(jié)構(gòu)，所以本文采取連續(xù)多次的對(duì)換操作，來(lái)增強(qiáng)變異的效果。
3.4 更新
　　本文采用代間更新的方式，由代溝G控制每一代群體中個(gè)體被更新的百分比，在t代N個(gè)個(gè)體中有(1-G).N個(gè)適應(yīng)度最高的個(gè)體被選擇完全復(fù)制到t+1代中去，即每代只產(chǎn)生N*G個(gè)新個(gè)體。代間更新的方式為遺傳算法利用優(yōu)化過(guò)程中的歷史信息提供了條件，加快了遺傳算法的收斂過(guò)程，但當(dāng)代溝過(guò)小時(shí)，可能會(huì)造成遺傳算法的過(guò)早收斂，G一般取0. 3～1，本文取0. 8。
3.5 適應(yīng)度函數(shù)
??? 由于遺傳算法是一種在給定的解空間內(nèi)不受約束的隨機(jī)搜索算法，因此必須構(gòu)造一個(gè)精確的適應(yīng)度函數(shù)指導(dǎo)遺傳算法的搜索方向向著最優(yōu)解逼近。本文中適應(yīng)度函數(shù)由目標(biāo)函數(shù)和懲罰函數(shù)組成，定義如下：
?
其中:B1、B2、B3是懲罰因子，通常取較大的數(shù)，以加大懲罰力度。
??? 計(jì)算個(gè)體的適應(yīng)度，需要用譯碼器對(duì)個(gè)體進(jìn)行解碼，求出其對(duì)應(yīng)的網(wǎng)絡(luò)結(jié)構(gòu)，然后調(diào)用潮流計(jì)算程序計(jì)算出節(jié)點(diǎn)電壓和支路電流代入公式（5）即計(jì)算出個(gè)體的適應(yīng)度值。當(dāng)個(gè)體違反電流和電壓的約束條件時(shí)，由于懲罰因子取的比較大，其適應(yīng)度值將非常的低，從而很容易在進(jìn)化過(guò)程中被淘汰。

4 遺傳算法與局部尋優(yōu)算法的混合策略
??? 在基本遺傳算法中，存在著局部搜索能力差、收斂速度慢的缺點(diǎn)。如果在遺傳算法框架中加入適當(dāng)?shù)幕卩徲虻木植克阉鳈C(jī)制，使遺傳算法與傳統(tǒng)的、基于問(wèn)題知識(shí)的啟發(fā)式搜索技術(shù)相結(jié)合構(gòu)成一種全局和局部搜索相結(jié)合的混合遺傳算法，則可以保證在種群進(jìn)化的每一代，算法的解都是局部最優(yōu)解，再通過(guò)競(jìng)爭(zhēng)從局部最優(yōu)解中選擇產(chǎn)生出優(yōu)良解。
??? 本文對(duì)經(jīng)過(guò)交叉和變異后的染色體執(zhí)行連續(xù)多次的“連支前插”操作，來(lái)尋找染色體對(duì)應(yīng)解所在局部解空間的最優(yōu)點(diǎn)。首先通過(guò)解碼器將染色體解成支撐樹(shù)的形式T={t1t2t3t4...tn,l1l2...lm}。事實(shí)上樹(shù)支集合內(nèi)的排列排序和連支集合內(nèi)的排列順序的改變對(duì)于配網(wǎng)的結(jié)構(gòu)都不產(chǎn)生影響，即適應(yīng)度是不發(fā)生變化的，只有當(dāng)連支與自己所在環(huán)內(nèi)的其它樹(shù)支發(fā)生交換，也就是發(fā)生了支路交換，才對(duì)網(wǎng)絡(luò)結(jié)構(gòu)產(chǎn)生影響；連支前插法，就是將連支向前插入至樹(shù)支區(qū)內(nèi)，例如將組合T中的連支l1向前插至樹(shù)支t4的前面，T的組合變成{t1t2t3l1t4...tn,l2...lm}的形式，這樣將由于先加入而變成樹(shù)支，同一環(huán)內(nèi)排在最后的樹(shù)支將變成連支，因此實(shí)現(xiàn)了支路交換。
??? 本文使用的“連支前插”是一種爬山行為(朝著改進(jìn)的方向)和連續(xù)多次的“前插”操作，如果“前插”使串的適應(yīng)度提高，則執(zhí)行操作，如此反復(fù)，直至不能再前插為止，最后將重新形成組合替代原來(lái)的染色體。這一操作實(shí)際上使給定的串改良到它的局部極點(diǎn)，這種局部爬山能力與基本遺傳算法的全局搜索能力相結(jié)合在實(shí)驗(yàn)中顯示了良好的效果。如圖1，算法通過(guò)局部尋優(yōu)算子來(lái)修復(fù)通過(guò)雜交和變異產(chǎn)生的新個(gè)體，使它到達(dá)局部最優(yōu)點(diǎn)。圖1中父代個(gè)體X和個(gè)體Y產(chǎn)生出子代個(gè)體Z′，通過(guò)局部尋優(yōu)產(chǎn)生出最終個(gè)體Z。

5 配網(wǎng)重構(gòu)的混合遺傳算法流程
　　在給定配電網(wǎng)絡(luò)和數(shù)據(jù)后，應(yīng)用本算法求解最優(yōu)運(yùn)行方案的步驟如下：
　　a.算法首先讀入原始數(shù)據(jù)進(jìn)行初始化，設(shè)定遺傳算法的最大進(jìn)化代數(shù)，群體規(guī)模N，代溝G,染色體長(zhǎng)度，雜交概率，變異概率等參數(shù)。
　　b.采用支路整數(shù)編碼方法隨機(jī)產(chǎn)生第一代的初始種群作為父代。并對(duì)初始群體的個(gè)體進(jìn)行解碼，調(diào)用潮流計(jì)算程序，計(jì)算個(gè)體適應(yīng)度及群體平均適應(yīng)度。
　　c.基于賭輪選擇機(jī)制從交代中選擇適應(yīng)度較高的個(gè)體進(jìn)行交叉操作，產(chǎn)生新一代個(gè)體。
　　d.對(duì)子代個(gè)體執(zhí)行變異操作。
　　e.對(duì)子代個(gè)體執(zhí)行“連支前插”操作，使個(gè)體得到進(jìn)一步的改良。
　　f.重復(fù)步驟c,d,e，直到子代個(gè)體數(shù)達(dá)到N*G個(gè)。
　　g.執(zhí)行代間更新操作，從父代中復(fù)制N*(1-G)個(gè)的適應(yīng)度最高的個(gè)體補(bǔ)充到子代中。
　　h.計(jì)算子代個(gè)體適應(yīng)度及群體平均適應(yīng)度，并將子代作為下一輪進(jìn)化的父代。
　　i.當(dāng)算法達(dá)到預(yù)先設(shè)定的最大進(jìn)化代數(shù)，算法將結(jié)束，并輸出適應(yīng)度最高的個(gè)體所對(duì)應(yīng)的網(wǎng)絡(luò)方案。否則轉(zhuǎn)到步驟c，繼續(xù)進(jìn)行進(jìn)化。

6 算例分析
　　本文算例采用一個(gè)33節(jié)點(diǎn)、5聯(lián)絡(luò)開(kāi)關(guān)的配電網(wǎng)測(cè)試系統(tǒng)[4]，如圖2所示。

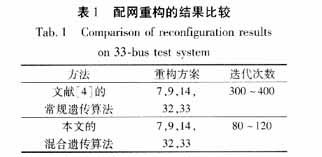
　　5個(gè)常開(kāi)聯(lián)絡(luò)開(kāi)關(guān)分別位于支路7～20、11～21，8～14，17～32，24～28上，假設(shè)所有支路都裝有分段開(kāi)關(guān)，按照文中的編碼方法，電源支路不參與重構(gòu)，一直是閉合狀態(tài)，不參與編碼，因此染色體長(zhǎng)度為35，群體規(guī)模取50個(gè)，交叉概率取0. 6，變異概率取0. 01。運(yùn)算程序后，最優(yōu)重構(gòu)方案為合上支路7～20、11～21，8～14，17～32上的分段開(kāi)關(guān)，斷開(kāi)6～7，8～9，13～14，31～32上的分段開(kāi)關(guān)。表1給出了運(yùn)算結(jié)果并與文獻(xiàn)4的算法計(jì)算結(jié)果進(jìn)行了比較。

　　本文算法與文獻(xiàn)[1]-[4]所述算法相比，其收斂性能有了很大的提高。采用文獻(xiàn)的基于二進(jìn)制編碼的遺傳算法，在同樣的算例上常常要進(jìn)行到300多代才能收斂，而采用本算法進(jìn)行到40多代就發(fā)現(xiàn)最優(yōu)個(gè)體，在100代左右其平均適應(yīng)度逐漸收斂于最優(yōu)，同時(shí)相對(duì)于文獻(xiàn)[1]-[2]，本文在每一代的計(jì)算效率也有很大提高。

7　結(jié)論
　　在采用遺傳算法來(lái)解決配網(wǎng)重構(gòu)中的大規(guī)模組合優(yōu)化問(wèn)題時(shí)，本文采用支路整數(shù)編碼方法實(shí)現(xiàn)基因編碼和基于構(gòu)造支撐樹(shù)方法的譯碼器設(shè)計(jì)方法，避免了生成不可行解的情形，減少了算法的無(wú)效搜索，提高了計(jì)算效率。同時(shí)本文還提出了基于圖論的連支前插法的局部尋優(yōu)算法，將它作為一個(gè)局部尋優(yōu)算子加入到算法中，提高了算法的局部尋優(yōu)性能，加快了算法的收斂速度。算例結(jié)果表明這種方法是可行、有效的。