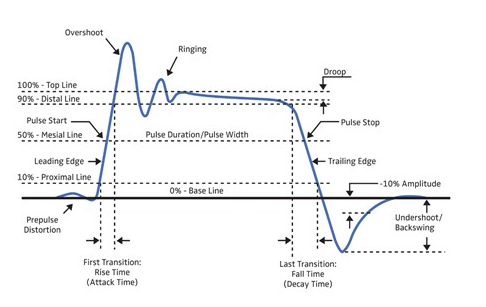
波特圖分析
用包含三個極點和一個零點的波特圖(圖11:波特圖)來分析增益和相位裕度。
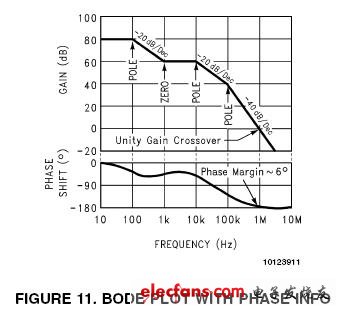
圖11
假設直流增益(DC gain)為80dB,第一個極點(pole)發生在100Hz處。在此頻率,增益曲線的斜度變為-20dB/十倍頻程。1kHz處的零點使斜度變為0dB/十倍頻程,到10kHz處斜度又變成-20dB/十倍頻程。在100kHz處的第三個也是最后一個極點將斜度最終變為-40dB/十倍頻程。
圖11中可看到單位增益點(Unity Gain Crossover,0dB)的交點頻率(Crossover Frequency)是1MHz。0dB頻率有時也稱為回路帶寬(Loop Bandwidth)。
相位偏移圖表示了零、極點的不同分布對反饋信號的影響。為了產生這個圖,就要根據分布的零點、極點計算相移的總和。在任意頻率(f)上的極點相移,可以通過下式計算獲得: 極點相移 = -arctan(f/fp) (6)
在任意頻率(f)上的零點相移,可以通過下式計算獲得: 零點相移 = -arctan(f/fz) (7)
此回路穩定嗎?為了回答這個問題,我們根本無需復雜的計算,只需要知道0dB時的相移(此例中是1MHz)。
前兩個極點和第一個零點分布使相位從-180°變到+90°,最終導致網絡相位轉變到-90°。最后一個極點在十倍頻程中出現了0dB點。代入零點相移公式,可以計算出該極點產生了-84°的相移(在1MHz時)。加上原來的-90°相移,全部的相移是-174°(也就是說相位裕度是6°)。由此得出結論,該回路不能保持穩定,可能會引起振蕩。
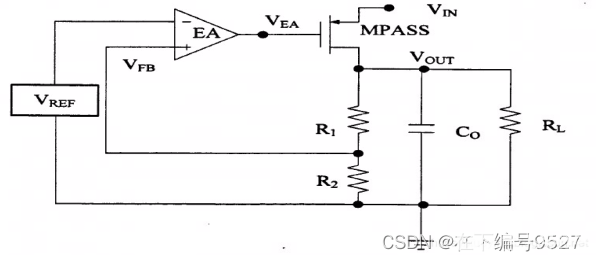
NPN 穩壓器補償
NPN 穩壓器的導通管(見圖1)的連接方式是共集電極的方式。所有共集電極電路的一個重要特性就是低輸出阻抗,意味著電源范圍內的極點出現在回路增益曲線的高頻部分。
由于NPN穩壓器沒有固有的低頻極點,所以它使用了一種稱為主極點補償(dominant pole compensation)的技術。方法是,在穩壓器的內部集成了一個電容,該電容在環路增益的低頻端添加了一個極點(圖12:NPN穩壓器的波特圖)。
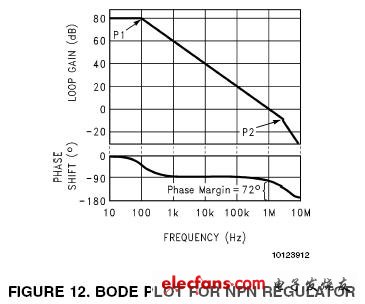
圖12
NPN穩壓器的主極點(Dominant Pole), 用P1點表示, 一般設置在100Hz處。100Hz處的極點將增益減小為-20dB/十倍頻程直到3MHz處的第二個極點(P2)。在P2處,增益曲線的斜率又增加了-20dB/十倍頻程。P2點的頻率主要取決于 NPN 功率管及相關驅動電路, 因此有時也稱此點為功率極點(Ppower pole)。另外,P2點在回路增益為-10dB處出現,也就表示了單位增益(0dB)頻率處(1MHz)的相位偏移會很小。
為了確定穩定性,只需要計算0dB頻率處的相位裕度。
第一個極點(P1)會產生-90°的相位偏移,但是第二個極點(P2)只增加了-18°的相位偏移(1MHz處)。也就是說0dB點處的相位偏移為-108°,相位裕度為72°,表明回路非常穩定。
需要兩個極點才有可能使回路要達到-180°的相位偏移(不穩定點),而極點P2又處于高頻,它在0dB處的相位偏移就很小了。
LDO 穩壓器的補償
LDO穩壓器中的PNP導通管的接法為共射方式(common emitter)。它相對共集電極方式有更高的輸出阻抗。由于負載阻抗和輸出容抗的影響在低頻程處會出現低頻極點(low-frequency pole)。此極點,又稱負載極點(load pole),用Pl表示。負載極點的頻率由下式計算獲得:
F(Pl) =1 / (2π × Rload × Cout) (8)
從此式可知,LDO不能通過簡單的添加主極點的方式實現補償。為什么? 先假設一個5V/50mA的LDO穩壓器有下面的條件,在最大負載電流時,負載極點(Pl)出現的頻率為:
Pl = 1 / (2π × Rload × Cout)=1/(2π × 100 × 10-5)=160Hz (9)
假設內部的補償在1kHz處添加了一個極點。由于PNP功率管和驅動電路的存在,在500kHz處會出現一個功率極點(Ppwr)。
假設直流增益為80dB。在最大輸出電流時的負載阻值為RL=100Ω,輸出電容為Cout =10uF。
使用上述條件可以畫出相應的波特圖(如圖13:未補償的LDO增益波特圖)。

圖13
可以看出回路是不穩定的。極點PL和P1每個都會產生-90°的相移。在0dB處(此例為40kHz),相移達到了-180°為了減少負相移(阻止振蕩),在回路中必須要添加一個零點。一個零點可以產生+90°的相移,它會抵消兩個低頻極點的部分影響。
因此,幾乎所有的LDO都需要在回路中添加這個零點。該零點一般是通過輸出電容的等效串聯電阻(ESR)獲得的。
使用 ESR 補償 LDO
等效串聯電阻(ESR)是電容的一個基本特性。可以將電容表示為電阻與電容的串聯等效電路(圖14:電容器的等效電路圖)。

圖14
輸出電容的ESR在回路增益中產生一個零點,可以用來減少負相移。零點處的頻率值(Fzero)與ESR和輸出電容值密切相關:
Fzero = 1 / (2π × Cout × ESR) (10)
再看上一節的例子(圖13),假設輸出電容值Cout =10uF,輸出電容的ESR = 1Ω。則零點發生在16kHz。圖15的波特圖顯示了添加此零點如何使不穩定的系統恢復穩定。
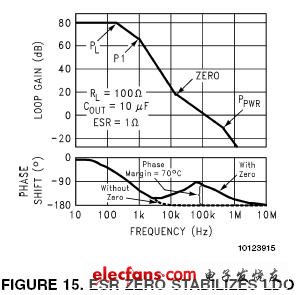
圖15
回路的帶寬增加了,單位增益(0dB)的交點頻率從30kHz移到了100kHz。到100kHz處該零點總共增加了+81°相移(Positive Phase Shift)。也就是減少了極點PL和P1造成的負相移(Negative Phase Shift)。 極點Ppwr處在500kHz,在100kHz處它僅增加了-11°的相移。累加所有的零、極點,0dB處的總相移為-110°。也就是有+70°的相位裕度,系統非常穩定。
這就解釋了選擇合適ESR值的輸出電容可以產生零點來穩定LDO系統。
 電子發燒友App
電子發燒友App










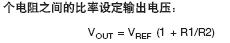













評論