盲源分離是指在信號的理論模型和源信號無法精確獲知的情況下,如何從混迭信號(觀測信號)中分離出各源信號的過程。盲源分離和盲辨識是盲信號處理的兩大類型。盲源分離的目的是求得源信號的最佳估計,盲辨識的目的是求得傳輸通道混合矩陣。
1 引言
盲源分離主要分為線性混疊和非線性混疊兩種。非線性混疊的主要有通過對線性模型的擴展和用自組織特征映射的方法[8]。
對于振動信號的盲分離,從2000年才開始受到重視[9],并且研究的范圍主要在旋轉機械和故障診斷中。
2 盲源分離基本概念
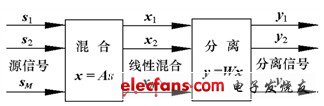
盲源分離問題可用如下的混合方程來描述[4]:
?
圖1 線性盲源信號分離框圖
事實上,在盲的范疇里,人們不可能實現源信號的完全恢復。盲源信號分離的求解結果有兩個不確定性:分離后信號向量的排列位置可以變化、信號的幅值與初始相位可以變化。很明顯,這樣的不確定性對源信號的分離不會有任何實質的影響。
3 振動信號盲分離的常用算法
3.1 最大似然準則算法
最大似然估計是要找到矩陣W使得所估計的輸出y的概率密度函數(PDF)與假設的源信號的PDF盡可能接近,是一種非常普遍的估計方法。
3.2 最小互信息準則及其算法
基于信息理論的最小化互信息的基本思想是選擇分離矩陣W, 使輸出y的各分量之間的互依賴性最小化,在理想情況下趨于零。
3.3 基于高階累積量的方法
Cardoso提出了應用四階矩進行盲信號分離的方法。在這個基礎上,人們從度量的非高斯性出發,得到快速的定點盲源抽取算法。另外Tong和Liu通過正交變換,對觀測到的混迭信號的四階矩進行奇異值分解(SVD),得到一類擴展的四階盲辨識和多未知信號提取算法。Cardoso還提出了基于四階累積量的聯合對角化。獨立成份分析方法中的峭度與負熵也是基于高階累積量的盲源分離方法。
3.4 非線性混疊盲源分離
大多數的盲源分離算法都假設混疊模型是線性的,更為準確的模型應當是非線性的或弱非線性的。人們針對非線性混疊模型提出了以下幾種方法:(1) 基于兩層感知器網絡的感知器模型法[20];(2) 基于自組織特征映射的無模型方法;(3)徑向基函數網絡法,這種方法魯棒性較好。
4 振動信號盲源分離方法的探討
4.1 估計分離矩陣的加速梯度法
在最小化互信息準則的基礎上,有關研究推導分析出加速梯度法的計算步驟,然后對轉子的振動信號進行采集并盲分離,得到了滿意的結果。
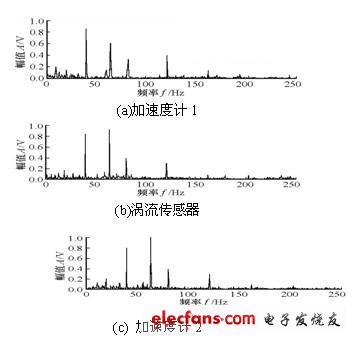
在一個轉子試驗臺上安裝2個加速度計和1個渦流傳感器采集信號,得到的傳感器信號與分離結果的功率譜,如圖2和圖3所示。
?
圖2 各傳感器采集的混合振動信號的功率譜
分析表明,基于最小化互信息原理的加速梯度法能夠較好地估計出分離矩陣, 其實現步驟可行。
?
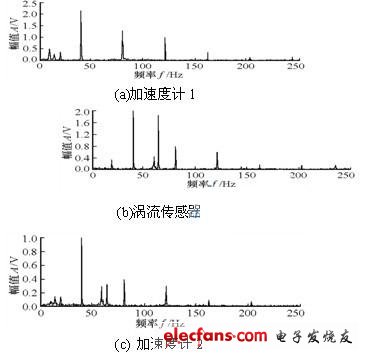
圖3 分離后各傳感器振動信號的功率譜
對具有故障的實際轉子進行多傳感器信號采集并進行盲分離,結果表明:采集信號中混疊的不同故障特征能夠較好地分離開來,分離后各傳感器信號的功率譜圖基本上只顯示出一種故障特征。但是旋轉激勵的影響不能從盲源分離的結果中完全消除。
4.2 卷積混合盲分離時域方法
有許多文獻用卷積混合矩陣模型對BSS進行了研究。基于時域信號的盲分離[24]方法對數值信號進行卷積混合并進行盲識別,如圖4所示。混合后兩個源信號分離結果說明所用算法在低頻段可給出好的分離結果,且可分離信號中的諧波信號[25]。
實際工程中的信號源個數是不明確的。可在人為設定源信號個數m的基礎上,進行隨機迭代,最大化各個分離信號y(n)。
對動力機械結構的不同位置上安裝5個傳感器,進行振動信號采集,并對采集信號用卷積混疊矩陣進行盲分離。結果表明,靠近激勵源的兩個傳感器(4、5兩個傳感器)得到的信號被方便地分離出來,而其他測點的傳感器采集信號難以收到理想的分離結果。這與理論方法是一致的。
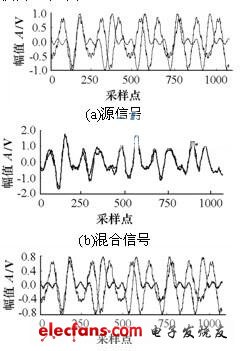
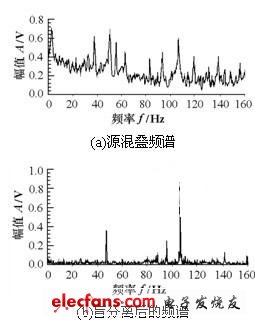
第5個傳感器的原始信號和分離結果如圖5所示。可看出,實際的信號在時域和頻域都難以直接觀察出來。進行盲分離,得出兩個典型的周期信號及一個隨機信號。圖5(b)是兩個周期信號合成的頻譜。兩個周期信號分別是發動機、電機旋轉頻率[26]。實際振動信號進行的源信號盲分離表明,所用方法在機械振動信號盲源分離中是適用的,信號得到較好的分離。
?
圖4 兩個諧波信號的分離
?
圖5 實際振動信號的盲分離
4.3 基于峭度的快速定點算法
經典的測量非高斯方法是峭度(kurtosis)或稱四階累積量。有關研究用基于峭度的快速定點算法對真實的轉子振動信號進行了盲源分離研究。在轉子振動試驗臺上安裝4個加速度傳感器,三個加速度傳感器是安裝在軸承座上的,另一個安裝在垂直于轉子軸的連接盤上以便測量軸向的振動情況。試驗時的轉速為525轉/分。由此得到4個采集信號。
值得注意的是,實際采集的信號一般就是混合后的信號。所以前述數值仿真分析方法中,“信號混合”這一步就不需要了,可以在直接對采集的信號進行預白化處理后,再用基于峭度的快速定點抽取算法進行分離。
?
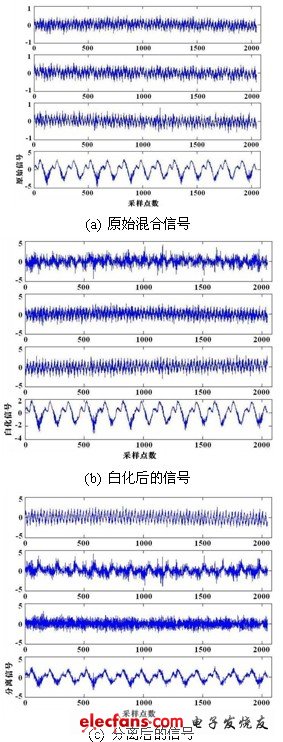
圖6 轉子振動信號的盲源分離
由傳感器測得的4個振動源信號如圖6(a)所示;預白化處理后的信號、分離后的信號分別如圖6(b)、(c)所示。從圖6(a)可看出,從原始的轉子振動信號中只能分辨出軸向沖擊信號,而其他3個信號波形十分相近,無法識別出哪個信號是哪個振動源產生的。從圖6(c)中能夠清晰地分離出不同的振動信號源。第四個信號是明顯的軸向沖擊信號,第二個信號是轉子旋轉的信號,第一個信號是軸承滾子的沖擊信號,第三個信號是噪聲信號。這說明用基于峭度的快速定點算法對轉子振動信號的盲源分離是十分有效和成功的。
4.4 改進的基于Jacobi優化的極大似然估計方法
在傳統的Jacobi優化算法的基礎上,文獻[10]探索了一種具有初始化四階矩矩陣的優化算法,來提高算法的收斂速度和計算效率。
用6個模擬源信號進行混合,分別用FastICA算法、JADE算法來與改進Jacobi優化算法進行比較,采取采樣點數從5000變化到30000,來依次統計各個算法的計算時間。3種算法的計算效率如圖7所示。可以看出JADE算法的計算時間相比于其它兩個算法要長,這在大采樣點情況下表現更為明顯,而基于初始化四階矩矩陣的算法與FastICA算法有著接近的計算時間(相差3%左右)。

?
圖7 三種算法的計算效率
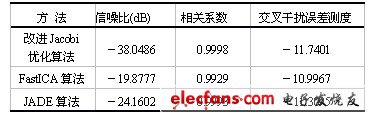
利用仿真試驗來分析各個算法分離信號的信噪比、相關系數以及交叉干擾誤差測度,如表1所示。這三個指標的值越大表明算法實現的分離信號就越逼近源信號,分離的性能就越優良。從表1可以看出,該算法可以得到優于其它兩個算法的信噪比、相關系數以及交叉干擾誤差測度。所提出的算法在分離信號的性能指標上遠優于FastICA算法。
4.5 魯棒的二階非平穩源分離方法
D. T.Pham對于一組對稱正定矩陣{Mi}提出了一個不同的準則,它不需要進行任何預白化,而且對角化矩陣同時也是分離矩陣[30]。對于有不同功率譜(或等價于不同的自相關函數)的有色源,可以使用時滯協方差矩陣,并由此得到了二階盲辨識(SOBI)算法。Choi和Cichocki對非平衡源SOBI進行修改,提出一種高效靈活的二階非平穩源分離(SONS)方法 [31]。
表1 各個算法分離信號的性能指標
?
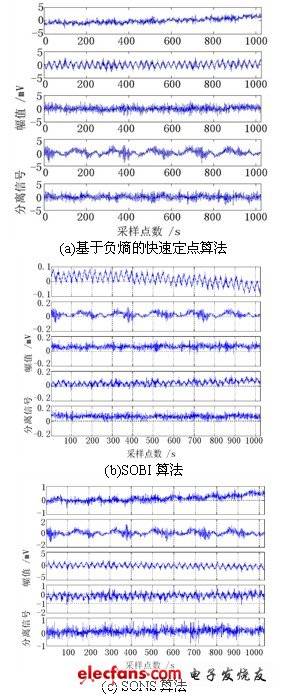
用與4.3節相同的實驗臺,用SONS算法對噪聲含量較少的轉子系統中低轉速數據進行分離,與基于負熵的快速定點算法相比,SONS算法在分離效果上的改善很小。在含有大量噪聲的高速旋轉情況下,基于負熵的快速定點算法對轉子振動信號的分離結果如圖8(a),在改用SOBI算法后,分離結果得到了改善,如圖8(b)。而在改用SONS算法,分離結果的改善則很明顯,如圖8(c) [32]。
?
圖8 用三種算法對高速數據盲源分離結果的比較
5 結論
本文介紹的內容為將盲源信號分離技術應用于機械振動信號的故障診斷提供了一個依據,也為盲源信號分離應用于實際工程信號的處理打下了基礎。
 電子發燒友App
電子發燒友App






















評論