無線傳感器網絡是由大量隨機分布的傳感器節點組成,是一種分布式的、自組織的網絡。其關鍵技術包括:網絡拓撲控制、節點定位、時鐘同步、數據融合、路由協議等。而節點定位問題則是無線傳感器網絡中的一個最為基本和重要的問題。目前,無線傳感器網絡定位算法可以分為基于測距和基于非測距的定位算法。基于測距定位常用的測量方法有TOA、TDOA、AOA、RSSI,盡管這些技術相對精度高,但是對硬件要求很高。基于非測距定位常用的測量方法有:DV- Hop、質心、APIT、MDSMAP。
DV-Hop為典型的基于非測距定位,其對硬件要求低,實現簡單。它的不足之處在于計算平均跳距及定位坐標時會產生誤差。因此針對DV-Hop算法的缺陷,提出了一系列的改進算法,包括:對原始算法中的平均跳距進行改進,使用多個錨節點估算平均距離并且采用歸一化加權的平均跳距;提出基于幾何學的定位算法,利用幾何學中的斜率方法來判斷錨節點間的位置關系,從中選取最優的錨節點序列,從而更精確地確定未知節點;引入共線度的概念,利用共線度參數,動態地調節未知節點可以收集的鄰居錨節點的距離閾值,挑選網絡中好的錨節點組進行位置估計,最后再用加權估計機制來得到最終的節點位置估計。這些方法都在一定程度上提高了定位精度。
本文針對DV-Hop算法中計算平均跳距和三邊定位兩方面存在的定位誤差,提出了改進的算法。首先利用全網平均跳距來糾正單個錨節點的平均跳距,然后在最后計算三邊定位時,利用節點間連通度的不同,選擇最優組合的3個錨節點來參與定位,進一步提高定位精度。
1 DV-Hop算法介紹
美國路特葛斯大學的Dragos Niculescu等人利用距離矢量路由和GPS定位原理提出一系列分布式定位算法,合稱APS,DV-Hop算法就是其中的一種。
DVHop分為3個步驟實現:
① 錨節點i廣播自身的位置信息IDi。初始跳數0,每發送一個節點信息,跳數就加1,然后轉發,直到網絡中所有的節點都收到錨節點的信息包。如果節點收到同一個錨節點不同的跳數信息,只取最小的跳數信息。
② 當錨節點i接收到其他錨節點的位置和最小跳數信息后,就可以計算出平均每跳距離(Average Hop Distance, AHD)的計算公式:
其中,(xi,yi)、(xj,yj)分別為錨節點i、j的坐標;hij為兩個錨節點之間的跳數。未知節點只接收離它最近的錨節點的AHDi,hopi為未知節點離最近錨節點的跳數,再根據跳數信息,即可算得未知節點與錨節點的距離P:
③ 當未知節點獲得3個或者更多的錨節點信息時,可以利用三邊定位或者最大似然相似求出未知節點的位置。(x,y)為未知節點的坐標,(xi,yi)為已知錨節點的坐標。根據式(2)即可算出未知節點的坐標:
2 改進后的DV-Hop算法
本文主要對DV-Hop算法里的第2步和第3步進行改進,第1步與原算法相同。原算法中,在第2步計算平均跳距的時候,未知節點接收來自最近的錨節點的平均跳距。但是由于網絡節點分布的不均勻性,導致單個錨節點計算的平均跳距存在著一定的誤差,因此本文引入全網平均跳距與單個錨節點平均跳距的均值來修正原算法中的平均跳距。在第3步中,錨節點的位置信息對定位精度影響很大,本文利用節點間連通度的不同,選取最優的3個錨節點,以減小定位誤差。
2.1 平均跳距的改進
將全網平均跳距與單個錨節點估算出來的AHDi取平均來代替經典算法中的平均跳距,這樣未知節點既有全網的估算信息,也具有離它最近的錨節點的估算平均跳距AHDi的局部信息。全網平均跳距公式為:
其中,n為網絡中的錨節點的個數。
修正后的平均跳距AHD公式為:
2.2 基于選擇性的3個錨節點
基于選擇性的錨節點的定位算法[15]利用連通度的不同,在三邊節點定位時,選擇最優的3個錨節點定位,使其定位誤差最小。
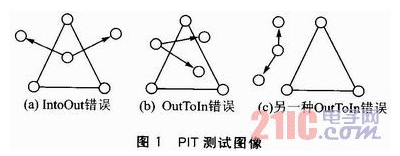
節點分布圖如圖1所示。未知節點N1利用三邊定位時可以用不同的3個錨節點組(P1,P2,P3)、(P1,P2,P4)、(P2,P3,P4)、 (P1,P3,P4)來定位。而用最大似然估計計算時,則選用(P1,P2,P3,P4)來定位,這樣不同的錨節點組肯定會產生不同的定位位置。
圖1 節點分布圖
2.2.1 基本規則
用未知節點與每個錨節點的最小跳數來定義連通度,用數組來表示。比如N1到所有錨節點的連通度為[1,1,2,5]。這樣圖1中的所有的未知節點的連通度可以用數組表示,如表1所列。
表1 未知節點的連通度
用未知節點之間連通度差的絕對值的和來定義連通度的不同,比如N1與N2之間連通度的不同為∣1-2∣+∣1-1∣+∣2-1∣+∣5-4∣=3。這樣可以計算N1到其他所有未知節點的連通度的不同,如表2所列。
表2 N1到未知節點連通度的不同
由表2可以得出,N2、N3到N1連通度不同為3、4,而N4、N5到N1連通度不同為9、11。說明N1離N2、N3更近。這一點也可以從圖1中看出。
2.2.2 確定最優的3個錨節點
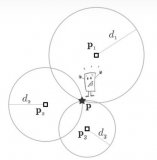
圖2 選擇性錨節點的節點分布圖
選擇性錨節點的節點分布圖如圖2所示。未知節點Nx代表未知節點的實際位置,N(i,j,k)為根據3個錨節點組合所估算的位置,R為節點的通信半徑,An是離N(i,j,k)最近的錨節點,Am為通信范圍R之外的任意錨節點。
An的位置情況有3種:在0?5R的通信范圍內;在0?5R~R的通信范圍內;在R通信范圍之外。這樣計算AHD(i,j,k),m就有3種可能:
其中,AHD(i,j,k),m為根據3個錨節點組合所估算的位置節點與錨節點Am之間的平均跳距,AHDn,m為錨節點An與錨節點Am之間的平均跳距,AHDm為錨節點Am的平均跳距。
N(i,j,k)與錨節點Am之間的距離P(i,j,k),m可以計算出來,那么就可以算出N(i,j,k)與錨節點Am之間的跳數hop(i,j,k),m,公式為:
假設一共有n個錨節點,這樣N(i,j,k)與Nx計算出來的連通度的不同可以表示為
Nx選出最小的連通度不同的節點是最為靠近Nx的節點(即定位的誤差最小)。
3 算法仿真實驗
為了驗證算法理論的可行性,在100 m×100 m的區域中,對提出的改進的DVHop算法用Matlab7.0進行實驗仿真,將實驗結果與原DVHop算法和參考文獻[12]的算法進行對比分析。仿真數據隨機運行50次,最后取平均值。
3.1 測距誤差
測距誤差是指節點間的估算距離與實際距離的差值。在100 m×100 m的區域中,隨機分布100個節點進行仿真實驗,其中有一部分部署的是錨節點,是能夠獲知自身位置信息的節點,且錨節點和未知節點具有相同的通信半徑。通過設置不同的錨節點比例和節點通信半徑,比較改進的算法與原DVHop算法對測距誤差的影響。圖3為通信半徑為10 m時的測距誤差,圖4為通信半徑為20 m時的測距誤差。
圖3 通信半徑為10 m時的測距誤差
圖4 通信半徑為20 m時的測距誤差
在同等條件下,改進的測距誤差始終是低于原DVHop算法的,且不同的通信半徑對測距誤差也會產生不同的結果。圖3中,通信半徑為10 m,改進后的算法平均測距誤差比原算法降低1.45 m;圖4中,通信半徑為20 m,改進后的算法平均測距誤差比原算法降低1.67 m。這是因為隨著通信半徑的變化,會對節點間的跳數和平均跳距產生影響。由于本文改進后的算法是用全網的平均跳距代替單個節點的平均跳距,這樣使得對平均跳距的估計更為準確,估算距離也就越準確,越接近實際的距離。
3.2 定位誤差
定位誤差(Localization Error,LE)是指通過定位算法測量估計的坐標與實際坐標之間的差值。用這種差值除以節點的通信半徑,就是定位誤差率。計算方法如下:
其中,(x,y)為未知節點的實際坐標,(xi,yi)為定位算法所估計出來的坐標;R為節點的通信半徑。
圖5和圖6是節點總數分別為100和300、節點通信半徑為10 m時,本文改進算法、DVHop算法和參考文獻[12]中的算法三者在錨節點比例不同時的定位誤差比較結果。從兩幅圖中可以看出,在相同的半徑和錨節點的環境下,改進算法的定位誤差率要低于DVHop算法和參考文獻[12]中的算法。但是在錨節點比例較低的情況下,節點的定位誤差較大。這是因為錨節點較少時,未知節點與錨節點之間的距離變遠,導致計算平均距離時會產生很大的誤差。因此隨著錨節點比例的增加,能夠有效地減小定位誤差。
圖5 中,當錨節點的比例為30%時,DVHop的定位誤差率為43.25%,參考文獻[12]算法的定位誤差率為33.37%,而本文改進算法的定位誤差率為 28.34%。圖6中,當錨節點的比例為30%時,DVHop的定位誤差率為26.89%,參考文獻[12]算法的定位誤差率為14.95%,而本文改進算法的定位誤差率為10.21%。由此說明,本文的改進算法要優于其他兩種算法。這是因為在參考文獻[12]中,只考慮了平均跳距一個因素對定位誤差的影響,而本文改進算法則是從平均跳距的改進和利用連通度的不同選取錨節點兩個方面考慮,使其定位誤差進一步地減小。
圖5 節點總數為100時的定位精度
圖6 節點總數為300時的定位精度
結語
本文首先介紹了DVHop算法的基本思想,針對經典的DVHop算法中存在的定位精度不高的缺陷,提出了兩點改進:
單個錨節點所估計的平均跳距來代替全網的平均跳距,會產生很大的誤差,因此平均跳距利用全網平均跳距與單個錨節點估計的平均跳距的均值來修正;
根據連通度的不同選擇最優的三個錨節點進行三邊定位計算,以提高定位精度。
仿真實驗數據表明,改進后的算法降低了測距誤差,定位誤差率進一步降低,從而提高定位精度。且在改進的過程中,沒有添加硬件成本。
 電子發燒友App
電子發燒友App











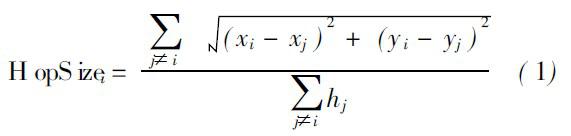










評論