嵌入式運動工程師必須知道智能電子設備如何放置在物理結構中（“嵌入式”）以及每個組件如何相對于彼此移動（“運動”）。在本文中，我想討論我們如何描述和建模后一個術語，運動，我們通常認為它非常簡單。

當我們設計運動系統時，我們會問如下問題：

運動穩定嗎？

我們怎樣才能讓動作更流暢、更優雅？

實現所需運動的最佳方法是什么？

為了以高技術可預測性回答這些問題，我們經常使用可信賴的運動學和動態模型。有時，我們在機械手冊、工程工具箱、維基百科或工程網絡上的其他地方找到的模型對于我們的場景來說已經足夠了。有時，它們不成立，我們需要一個具有更強預測能力的模型。

一句經常被引用的工程諺語說：“所有模型都是錯誤的。有些是有用的。” 毫無疑問，該原則也適用于 3D 運動。一些運動學和動力學模型在一種情況下可能是合適的，但在其他情況下則不夠。

對于運動，普遍適用的方程可以處理多方向的 3D 旋轉和平移物體，而簡單方程只能處理平移和單向旋轉。簡單的方程式很有吸引力，因為它們既快速又簡單。下面我將通過比較兩個系統來說明這個想法，這兩個系統需要不同的方法來建立適當的運動學模型。

簡單的運動分析

下圖顯示了一個簡單的齒輪系統。底部齒條驅動兩個齒輪和另一個齒條。讓我們假設兩個齒輪的中心是固定的，所以齒輪只是在旋轉，而頂部齒條在 x 方向上移動。如果底部齒條以ν 1 = 1mm/s 的速度移動，頂部齒條的移動速度有多快（假設齒輪沒有損失）？

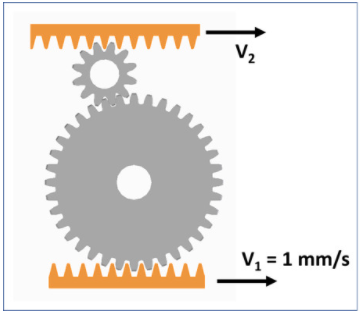
事實證明，我們需要的方程非常簡單。我們可以在這個例子中輕松定義角度信息：

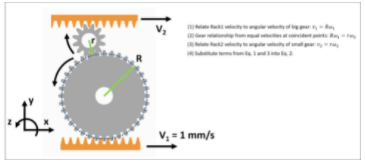
每個齒輪的角速度 （ ω ） 僅等于一個角度 （ θ ） 的時間變化率。例如，對于較大的齒輪，我們可以說它的角速度用ω 1 = θ? 1來描述。

每個齒輪都圍繞其質心旋轉。

通過將該系統本質上視為 2D，我們可以安全地在分析中使用ν = τω 。應用該關系來設計我們的系統會得出 ν 2 = ν 1。

轉向 3D

當我們遇到 3D 運動系統的零件在多個方向而不是圍繞其質心旋轉時，我們該怎么辦？我們如何定義角度？什么是角速度？

四軸飛行器的運動是更復雜的 3D 運動系統的一個合適示例。對于四軸飛行器，我們希望穩定地控制它的位置（“它在哪里？它的速度有多快？”）和空間方向（“‘傾斜’角度是多少？”）。飛行中的四軸飛行器可以在 x、y 和 z 方向上平移并圍繞 x、y 和 z 旋轉（其中 xyz 是固定在空間中的三個正交方向）。

為了保持四軸飛行器穩定，我們將使用陀螺儀測量每個軸的角速度，并將該信息反饋給控制算法。三軸陀螺儀將輸出三個角速度值，但請注意，這些角速度對應于四軸飛行器上固定的軸。這些 xyz 軸與與四軸飛行器在空間中的位置、速度和加速度相關的 xyz 軸不同。可以說，將陀螺儀的輸出轉換為可被控制算法消化的東西是 3D 動力學模型派上用場的地方。

開始使用更強大的 3D 模型

一個更強大的 3D 運動模型開始于：

將參考系分配給空間中固定的點。

將系統中的所有對象視為剛體。

為每個身體上的某個點分配一個參考系。

參考系是我所說的一組三個正交單位向量，它們連接到某個點。在本例中，唯一的對象是四軸飛行器，因此我們將其視為單個剛體。（我們將在這里忽略四軸飛行器上的其他部分。）我們會說參考系N 固定在地球上的一點，由n? x、 n? y和 n? z組成。我們將參考框架D附加到四軸飛行器的質心。參考系D由d? x、 d? y和 d? z組成。 上圖顯示了 CAD 中的簡化描述。

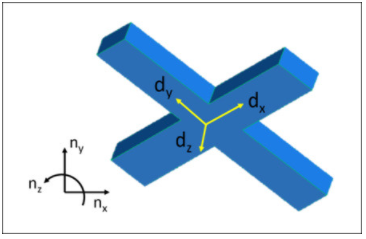
陀螺儀的測量結果將為我們提供關于d? x、 d? y和 d? z的角速度，對于控制算法，我們想知道這些值如何與n? x、n? y和n? z中的有意義的角度相關聯。 實現此目的的一種方法是通過圍繞固定在四軸飛行器機身上的軸進行一系列簡單旋轉來定義四軸飛行器的方向。在這一步的開始，我們可以用d? x、d? y和d? z來表示四軸飛行器的角速度，它看起來像這樣：

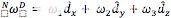
在這項工作的最后，我們將使用旋轉矩陣以歐拉角的形式表示每個角速度。歐拉角為我們提供了一種精確描述物體在 3D 空間中的方向的方法。（請注意，歐拉角不一定對應于我們所說的偏航、俯仰和滾動。）我們將以ω 1、ω 2和 ω 3的精確表達式結束。

由于四軸飛行器可以繞多個軸旋轉，我們不再有簡單的ω 1 = θ? 關系，也不能用ν = τω 來概括地描述四軸飛行器上一點的速度。事實上，ω 1的方程 看起來像 ω 1 = φ? = cos α + α? - θ? sin φ 其中θ、φ和α 是歐拉角。ω 2 和ω 3的方程 不幸的是，同樣混亂。簡而言之，很容易看出 3D 系統的定義如何超出我們在傳統動力學資源中發現的范圍。有關這些計算的更多詳細信息，請參閱額外信用部分。

模擬復雜的運動現象

當我們對復雜的 3D 運動現象建模時，區分標量和矢量是關鍵。請記住，向量既有大小又有方向（例如，東北方向 25 mph），而標量只有大小（25 mph）。當我們將其他物理值（速度、加速度、線性和角動量、力、扭矩等）帶入我們的模型時，我們應該首先將它們視為向量。例如，當我們談論扭矩時，指定它的方向（例如，關于正 z 軸）以及它的大小（5 Nm）是很有用的。

使用更復雜模型的好處是，您可以為任何由剛體組成的運動系統精確定義與角度相關的所有量（方向、角動量、力矩和慣性積等） 。方程可能會變得粗糙，因此使用 MATLAB、Working Model或MotionGenesis等軟件程序通常是明智的。

請注意，如果我在齒輪示例中遵循 3D 模型方法，那么我會明確地將速度和角速度視為矢量。但同樣，齒輪示例中的運動符合我簡化為 2D 運動學方程的標準，并且我避免了 3D 模型的時間繁重的定義。如果我有一個更復雜的運動系統，那么我必須將運動學和動態量視為向量，否則我可能會面臨預測模型不佳的風險。

對系統的運動進行精確建模可能是一件棘手的事情，但通過構建一個穩健的模型，我們可以更快地響應更廣泛的問題。如果我們希望制作一個功能強大、平滑且優雅的穩定運動系統，那么我們必須決定哪種模型更合適。作為工程師，我們必須認識到常見 2D 方程的局限性，以及解決 3D 運動系統的其他合適工具。

有關 3D 運動分析相關主題的更多資源和支持，請關注Simplexity 的產品開發博客。

額外學分

這是為四軸飛行器精確定義旋轉信息的一種方法：

我們將使用中間參考系來描述四軸飛行器的方向。我們將調用附加到四軸飛行器B的初始參考系。最初， b? x = n? x、b? y = n? y和b? z = n? z。參考系D仍然附著在身體上，最初，d? z = b? z = n? z。我們將首先圍繞b? z （這里等于d? z）旋轉，然后我們將旋轉角度 + θ。 然后我們可以寫出 B 在N中的角速度是

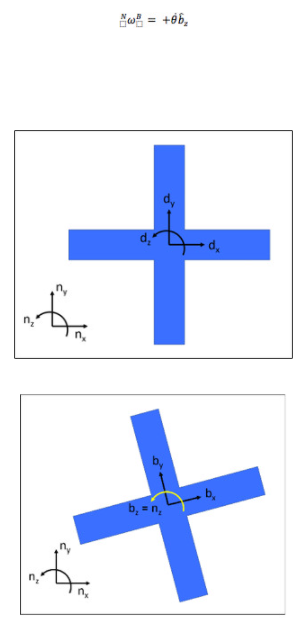
然后我們將圍繞身體上的另一個固定軸d? y旋轉，我們將把這個新的中間參考系稱為C。最初，? x = b? x、d? y = ? y = b? y和 ? z = b? z。 我們將圍繞 ? y旋轉角度 + φ。然后我們可以寫出 C 在 B 中的角速度是。

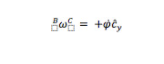
最后，我們將圍繞固定軸 d? x旋轉。最初，d? x = ? x，d? y = ? y和d? z = ? z 。我們將 圍繞d? x旋轉角度 + α。然后我們可以寫出D在C中的角速度是。

?

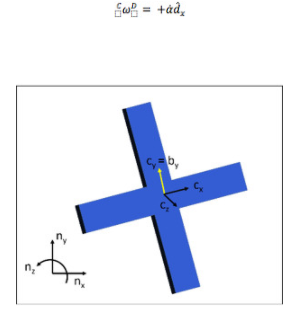
因為這是來自陀螺儀的數據格式。我們想根據我們的全球參考框架N重新表達這一點。

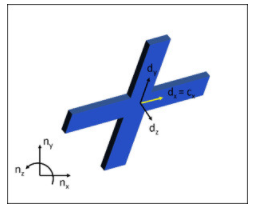
幸運的是，這些旋轉中的每一個都在每個中間幀之間創建了一個旋轉矩陣，我們可以使用這些旋轉矩陣的乘法來表達

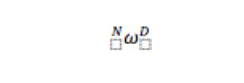
我們定義的角度。（我不會詳細介紹這部分，但它直接來自進行這些中間旋轉。）結果如下：

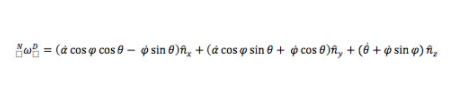
請注意，我們可以通過以 _ _ _ _ _ _ _ _ _ d? 1、d? 2和d? 3。此外（通過重新排列），我們可以用? 1、? 2和? 3來表示每個歐拉角。例如：

唉，我們為四軸飛行器的角速度給出精確定義并使其可供控制算法使用的第一步已經完成。

審核編輯：郭婷