王利娟 1，常 霞 1，張伯妍 2 （1.北方民族大學 寧夏智能信息與大數據處理重點實驗室，寧夏 銀川 750021； 2.北方民族大學 數學與信息科學學院 圖像處理與理解研究所，寧夏 銀川 750021）

摘??要：針對多尺度 Retinex 處理低照度圖像出現的“光暈偽影”和色彩泛白現象，文中提出一種基于自適應權重帶色彩恢復因子的多尺度Retinex圖像增強算法。在HSV顏色空間中先將亮度通道圖像分解為Retinex增強層和細節恢復層。在Retinex增強層中，不同尺度參數具有不同的增強效果，根據像素的概率分布，計算明暗不同區域的概率分布函數，獲得自適應權重。所提算法有效地克服了尺度參數對亮度信息恢復造成的過增強現象。

在細節恢復層中，導向濾波具有更優越的保邊去噪特性，故采用導向濾波將圖像分解成平滑層和邊緣層圖像，并利用增益系數增強邊緣層信息。最后將自適應權重后Retinex亮度增強層、平滑層和邊緣層圖像融合重構為增強后的亮度通道圖像，并在伽馬校正算法中融入自適應調節因子來恢復圖像在融合過程中丟失的部分細節和色彩信息。實驗數據表明所提算法較其他對比算法具有更明顯的優越性。 ?

在光照不足或天氣惡劣等條件下得到的圖像無法滿足人們對高清圖像的需求，而圖像增強算法可以改善圖像的視覺效果。濾波器算法是一種典型的具有保邊去噪特性的圖像增強算法。經典濾波器算法包括高斯濾波器、拉普拉斯高斯濾波器和雙邊濾波器[1]等。用高斯濾波增強圖像經常會出現過度模糊邊緣現象。雙邊濾波器[2?3]是一種對圖像像素的空間距離和亮度信息進行雙重考慮的非迭代的濾波算法，但對圖像中梯度變化大的部分，雙邊濾波核函數不穩定，極易出現梯度反轉現象。武昆提出一種將圖像的深度信息考慮在內的雙邊濾波器算法，增強結果具有較為清晰的輪廓和層次信息，但運算量較大，實時性也較差[4]。黃愛黎提出了對圖像進行逐點變換的局部拉普拉斯濾波算法[5]，此算法中存在大量的冗余信息，時間復雜度為O(N2)。

導向濾波器(Guided Image Filter，GIF)是由He K等人提出的一種時間復雜度只有O(N)的濾波算法，此算法很好地克服了雙邊濾波中出現的梯度反轉現象，該算法具有良好的保邊去噪性[6]。 Retinex [7?8]是基于人眼視覺感知特性而提出的一種增強理論。最初提出基于路徑[9?10]思想和基于偏微分思想[11]的Retinex圖像增強算法。這兩種算法有效地改善了低照度圖像的質量，但算法中的參數較多，極易引入外界噪聲；之后，學者們相繼提出基于變分思想[12?13]和基于中心環繞思想的Retinex算法[14?19]，這兩種算法很好地解決了因光照均勻這一假設所帶來的光暈現象。只是其中的變分法較為靈活，難以構造出滿意的目標函數。基于中心/環繞Retinex算法的增強結果具有較強的穩定性，所以被廣泛地使用于圖形圖像領域。算法中使用對數處理的方式可以極大地提升暗區域的像素值，對于光照不足的低質量圖像具有良好的增強效果。基于中心環繞的Retinex算法通常包括單尺度Retinex算法(Single?scale Retinex,SSR)[14?15],多尺度Retinex算法(Multi?scale Retinex，MSR)[16?17]和具有顏色恢復因子的MSR算法（Multi?scale Retinex with Color Restoration,MSRCR)[18?19]。其中SSR算法尺度較為單一，無法充分考慮到要增強的信息。

MSR算法是在SSR算法的基礎上又增加了兩個尺度的圖像增強算法。在 MSRCR算法中，增加了顏色恢復因子，在改善圖像局部細節信息和顏色保持方面取得了滿意的效果。但在處理某些顏色比例失衡的極端類型圖像時，顏色恢復因子依然無法精確地計算顏色之間的比例關系，增強結果經常趨于白化現象。同時MSRCR算法沒有充分考慮圖像的邊緣信息，增強圖像的邊緣處于模糊狀態。Li等人提出具有強魯棒性的 Retinex算法(Robust?Retinex)[20]，該算法具有較強的顏色保真效果，但圖像的局部細節信息并不清晰。 針對導向濾波器的保邊優勢以及MSRCR算法中存在白化現象的局限性，本文提出在 HSV色彩空間下，將亮度通道V 圖像分解為Retinex增強層和細節恢復層兩層。各層之間相互獨立增強圖像，互相彌補缺點并突出自身優勢[21]。在Retinex增強層中，自適應權重代替平均權重有效地提高了圖像的對比度和亮度，但光暈現象以及梯度反轉在圖像邊緣處引起的偽影不可避免。導向濾波的各向異性可以有效地保持圖像的邊緣信息。利用增益系數將原圖像與平滑層圖像相減所得到的邊緣層圖像進行增強。改進的伽馬矯正算法融合各層優勢，獲得具有清晰邊緣和色彩自然的增強圖像。

1 MSRCR 和導向濾波

1.1 MSRCR 算法

在光照均勻的條件下，Retinex理論認為物體表面的反射光對于人眼辨識顏色信息起著決定性作用，而外界的光照對于人眼獲取物體顏色信息并無太大影響。Retinex理論通常將圖像I(x,y)表示為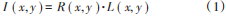： 式中：(x,y)表示圖像的像素；R(x, y)和L(x,y)分別表示光反射和光照度分量。為了方便計算，降低算法的復雜度，通常將式（1）用對數形式表示可以得到SSR算法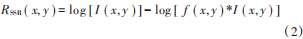： 式中:“*”表示高斯核卷積；f(x, y)通常表示高斯卷積核函數，滿足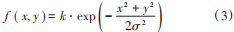： 式中：k滿足 ?f (x,y)dxdy=1;σ表示尺度參數。得到MSR算法

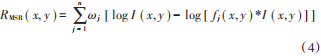
式中：n表示尺度數目，一般n=3；j表示不同的尺度數，一般有σ1,σ2,σ3；fj(x,y)為不同尺度參數下的卷積核函數；ωj是第j個參數所對應的權重因子，一般取均值。為解決圖像局部失真，引入色彩恢復因子Ci(x,y)，提出MSRCR算R：

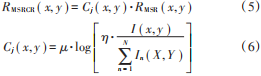
式中：μ和η分別是影響圖像色彩恢復的增益因子和偏移量，通常有μ=46,β=125。綜上所述，Retinex算法中，對于一幅低照度的RGB圖像，不同的尺度參數具有不同的增強效果，分別取小中大3個尺度（σ1=15,σ2=80,σ3=250）進行圖像增強實驗，增強結果如圖1所示。

圖1的增強結果顯示，當σ1=15時，局部對比度提升，但丟失了許多細節信息，色調變差；當σ1=250時，圖像的細節信息、亮度信息和顏色信息可保留更多；當σ1=80時，細節信息有所恢復，但亮度信息恢復不足。本文算法則利用自適應權重將不同尺度參數的優點進行融合，使得MSRCR算法的反射分量結果包含更多的細節內容。

1.2 導向濾波

導向濾波經常被用作圖像增強的預處理算法。假設引導圖像與濾波圖像之間滿足局部線性關系 [22]。將輸入圖像I，輸出的濾波圖像q通常用線性表示為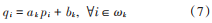： 式中：p為引導圖像；k為濾波窗口的中心位置；i為窗口中像素的索引；a和b表示線性函數的常數系數。對濾波圖像取梯度的時候，可得?q=a?p。可見當引導圖像有梯度，濾波圖像也會有梯度時，因此引導濾波對圖像具有良好的平滑保邊特性。為了計算ak和bk，定義損失函數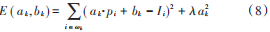： 式中λ屬于正則項。利用線性回歸可得到 ak和 bk的值：

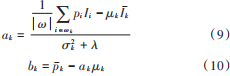
式中：μk和σ2k分別為窗口中引導圖像p的均值和方差；|ω|為窗口中像素的個數；Iˉk為輸入圖像I的均值。在濾波過程中，同一個像素在不同的窗口作用下會輸出不同的像素值，故需要計算它們的均值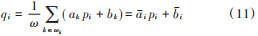： 導向濾波算法的最大優勢是濾波窗口的大小并不會影響算法的時間復雜度，因此在處理大型圖像時可以選擇較大的濾波窗口。原圖像減去濾波后的圖像可以得到邊緣細節圖像，本文算法便是利用該特性獲得邊緣層圖像，將邊緣層信息增強后再與濾波圖像進行重構得到新的細節恢復層圖像。

2 基于自適應權重的 MSRCR

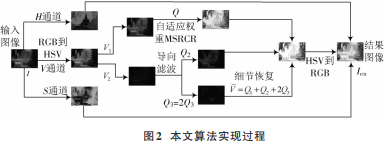
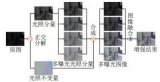
傳統的MSRCR算法通常會同時處理R，G，B三個顏色通道，所以三者之間通常會出現色彩比例不協調現象，導致增強結果呈現白化現象。在HSV顏色空間中，V通道分量包含了圖像大量的細節信息。不同的尺度參數會得到不同的增強結果，不能依賴傳統 MSRCR算法中三個尺度平均占比的思想。本文提出自適應權重的MSRCR算法，將V 通道分解為 Retinex 增強層V1和細節恢復層V2。利用自適應權重的MSRCR算法增強 V1，得到增強層結果Q1，利用導向濾波算法的保邊優勢增強V2，得到平滑層Q2和邊緣層Q3信息。這三層信息進行融合得到最終的增強結果V。算法實現過程如圖2所示。

2.1 圖像多層次分解 本文提出基于融合的思想調節圖像的照明問題。通常有一些成熟的算法具有特定的增強效果，例如CLAHE算法和濾波器分別改善圖像的局部對比度和噪聲，因此可以結合它們各自的優勢[23]。受此啟發，本文將V通道圖像進行分層，分別記為Retinex增強層V1 和細節恢復層V2，并設計兩個權重，滿足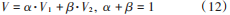： 分層后所得到的融合結果既要避免 V2 層邊緣放大造成過度卡通化，又要避免Retinex 算法出現的亮度過度增強導致增強結果出現白化現象。圖3為3組V?在不同權重下的融合結果對比圖。

由圖3可得，圖像Retinex增強層所占的比重較小時，融合結果呈現過分曝光趨勢，出現部分細節信息丟失現象；Retinex增強層所占的比重超過V1=0.8V時，融合結果的亮度保持效果呈現過度下降趨勢，出現部分細節模糊現象。當 Retinex 增強層所占的比重為 V1=0.8V時，塔和樹木的邊緣信息都得到了增強，圖像的對比度也得到了改善。故 Retinex 增強層所占的比重為V1=0.8V，細節恢復層所占比重為V2=0.2V 時的融合效果最好。

2.2 Retinex增強層

在MSRCR算法中，使用15，80和250三個尺度參數的高斯核對圖像V1通道進行高斯濾波。由圖1可知，大尺度所占比重較大時得到的增強結果最好。所以本文依據圖像像素明暗程度提出自適應權重的MSRCR算法。在[0,255]范圍內利用標準正態分布將圖像像素等區域分為暗像素點、中亮像素點和亮像素點3類,即暗區域[0,85]、中暗區域[85,170]和亮區域[170,255]。再分別取均值作為3個區域的代表值作為正態分布的期望值，即μ1=43，μ2=128，μ3=213。對圖像V1層的3類像素點進行似然概率[24]計算，則有：

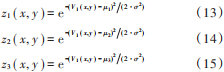
為得到原圖像的權重，根據這些概率值，將3個權重定義為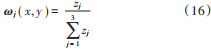： 自適應 MSRCR 具體實現如下：

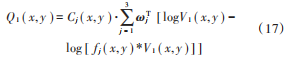
式中：Q1(x, y)為Retinex增強層的增強結果圖像；ωΤj為權重ωj的轉置。 綜上所述，從權重計算原理分析，該算法實現了對于大尺度占比較大、小尺度占比較少的目的，并且整個過程權重選擇是自適應實現的過程，有效地克服了上述MSRCR算法中均值權重的缺陷。圖4為自適應權重MSRCR算法前后的輸出結果。圖4c）顯示，自適應權重后的圖像對比度和亮度明顯提高，部分細節信息也均在。

2.3 細節恢復層

為進一步增強圖像的細節信息,對細節恢復層V2=0.2V通道圖像進行導向濾波，達到保邊去噪的效果。實驗步驟如下： 1）利用導向濾波模糊細節層圖像V2，得到模糊的平滑層圖像Q2； 2）細節層圖像V2減去平滑層圖像Q2得到的差值圖像，即為邊緣層圖像Q3，滿足:Q3= V2-Q2； 3）在細節層圖像V2上加上邊緣層圖像的一個權重部分即增益系數，滿足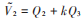： 此處的增益系數k不易過大，如果原圖像有任何零值或者選擇的k值過大，使得增益之后的峰值大于原圖像中的最小值時，這樣會導致最終的結果出現負灰度。負值將會導致邊緣周圍出現暗色暈輪，所以這里取k=2即可達到高度提升濾波的效果。實驗效果如圖5所示。 圖5e)、圖5f）顯示，邊緣增強后的V2結果比邊緣未增強的V2結果更加清晰，尤其是塔的柵欄處以及樹木的輪廓。最后將細節恢復層的結果V2與Retinex增強層結果Q1進行融合，融合過程如下： 對于融合之后出現的部分細節丟失和部分色彩顯示不自然現象，本文設計一種新的細節恢復方案，利用像素與像素鄰域均值的關系和伽馬矯正相結合的策略來恢復丟失的信息。

算法步驟如下： 1）對V進行歸一化，選擇一定大小的模板窗口m×n，通常選取3×3； 2）對于當前像素f (x,y )，計算其局部區域8鄰域均值 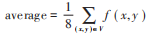3）利用增強強度s增強該點灰度值，提升對比度，滿足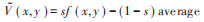： 4）利用伽馬矯正對V進行色彩恢復，滿足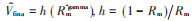： 式中：Vfina為恢復細節后融合圖像；Rm為V歸一化的均值；h為調節因子，圖像越暗則 Rm越小，h便增大。 5）最后將融合后的圖像轉換到RGB空間，得到RGB格式的增強圖像Ien。

3 實驗結果

將本文算法與SSR、MSR、MSRCR和Robust?Retinex[20]算法在Matlab 2018b的PC 端進行對比實驗。實驗結果如圖6~圖10所示。圖6~圖10的實驗結果：SSR算法的增強結果中顯示，雖然圖像的局部細節信息和局部紋理信息的質量有所改善，但對于圖像整體的對比度增強和亮度保持效果較弱，整體呈現視覺感知較暗現象，顏色信息恢復的也較少且存在局部色彩失真現象。圖6~圖8結果：基于MSR與MSRCR算法的增強結果中顯示，增強結果出現整體色彩偏紫的失真現象，不符合人眼的視覺特性。圖9、圖10中 ，基于MSR與MSRCR算法的結果顯示，增強結果趨于白化現象，整體較模糊，導致部分細節信息無法被清晰的顯示。圖6~圖9中基于Robust?Retinex算法的結果顯示，增強結果的色彩自然，亮度和對比度信息都有所恢復，但是依然存在細節信息丟失，整體呈現霧化視覺效果，圖像細節信息的清晰度下降。

?

圖10中基于 Robust?Retinex算法的整體增強效果良好，圖像的細節恢復較多；而本文算法的增強結果既不存在失真和白化現象，也不存在霧化模糊情況。在視覺感知上，本文算法結果整體上更加清晰自然，尤其對于圖像的色彩信息具有較強的恢復能力。增強圖像的結果除了主觀上的表達，還需要使用一些測量數據進行客觀評估，包括熵、Tenengrad[25]和平均梯度[26]。圖像熵是一種基于概率的強度分布統計信息，可以衡量圖像信息的豐富程度，公式如下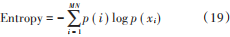： 式中：p (xi)代表像素值的概率；MN表示像素總數。 Tenengrad反映了圖像的清晰程度，公式如下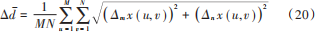： 式中：Δm x(u,v )和Δn x(u,v)分別是像素(u,v )水平與垂直方向上像素之間的差異。 平均梯度反映圖像對細節反差和紋理變化，公式為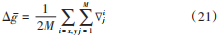： 式中?ij表示沿著i方向上在j位置上圖像的梯度值。圖像的客觀評估指標結果如表1~表5所示。

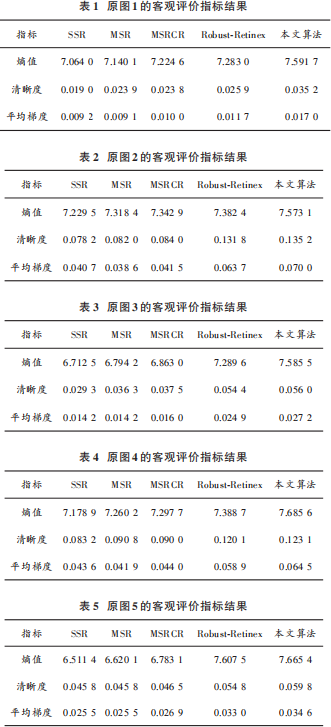
從表1~表5中的客觀數據的結果可知，5種算法的各個評價指標呈現遞增的變化趨勢，這是因為改進算法對于圖像的顏色信息以及對比度信息不斷改進，算法的細節內容在不斷的增強。而本文算法的熵值、清晰度、平均梯度指標比其他對比算法都大，都得到了提升。這說明本文算法恢復了更多的細節信息和顏色信息，具有較高的亮度保持度和色彩保真度。

4 結 論

針對基于MSRCR算法的低照度圖像增強結果趨于白化現象，本文提出一種自適應權重 MSRCR低照度圖像增強算法。所提算法有效地結合了Retinex算法和導向濾波器的優勢，并且對MSRCR算法中的平均權重進行改進，使得尺度參數在光照估計的過程中可以自適應調節，這樣既避免了圖像失真又平衡了亮度信息。利用增益系數對邊緣層增強之后再與平滑層結合能更有效地發揮導向濾波保邊去噪的優勢，有效地增強了圖像的細節信息。實驗結果顯示，無論是主觀評價還是客觀評價數據均表明，本文算法有效地提高了圖像對比度并突出了細節，有利于后續的圖像處理任務。 注：本文通訊作者為常霞。

參 考 文 獻 [1] 王慧琴 .數字圖像處理[M].北京：北京郵電大學出版社，2006. [2] 田小平，姜薇，吳成茂 . 基于雙邊濾波的低亮度圖像增強算法[J].西安郵電大學學報，2016，21（4）：43?47. [3] 常戩，賀春澤，董育理，等 .改進雙邊濾波和閾值函數的圖像增強算法[J].計算機工程與應用，2020，56（3）：207?213. [4] 武昆 . 基于邊緣保持濾波器的彩色圖像增強算法研究[D]. 長春：中國科學院，2017. [5] 黃愛黎 .快速局部拉普拉斯濾波器的研究與應用[D]. 昆明：云南大學，2018. [6] HE K，SUN J，TANG X. Guided image filtering [J]. IEEEtransactionson pattern analysis & machine intelligence，2013，35（6）：1397?1409. [7] YU X Y，LUO X Y，Lü G H，et al. A novel Retinex basedenhancement algorithm considering noise [C]// IEEE / ACISInternational Conference on Computer & Information Science.Wuhan：IEEE，2017：15. [8] 龍鑫 .基于 Retinex 理論的低照度圖像增強研究[D].重慶：重慶郵電大學，2019. [9] 代少升，劉琴，王斐，等 . 基于路徑的 Retinex 算法在紅外圖像增強中的應用[J].半導體光電，2015，36（3）：482?485. [10] SIMONE G，CORDONE R，SERAPIONI R P，et al. On edge?aware path ? based color spatial sampling for Retinex：fromtermite Retinex to light energy ? driven termite Retinex [J].Journal of electronic imaging，2017，26（3）：031203. [11] 余萍，郝成成 .基于分數階微分和多尺度 Retinex 聯合的霧靄圖像增強算法[J]. 激光與光電子學進展，2018，55（1）：280?285. [12] 董雪，林明星 . 基于變分結構引導濾波的低照度圖像增強算法[J].山東大學學報（理學版），2020，55（9）：72?80. [13] MA W，OSHER S. A TV Bregman iterative model of Retinextheory [J]. Inverse problems and imaging，2017，6（4）：697?708. [14] 趙冬梅，李斯娜 .改進單尺度 Retinex的彩色圖像增強算法[J].現代電子技術，2018，41（17）：71?75. [15] 王彥林，張進 .改進成像模型的單尺度 Retinex 彩色圖像增強算法[J].計算機工程與設計，2018，39（11）：3511?3515. [16] YANG X H，YANG J L. Research of image enhancementalgorithm based on multi ? scale Retinex [J]. Advances inintelligent systems and computing，2015，329：207?215. [17] ZOTIN A. Fast algorithm of image enhancement based onmulti ? scale Retinex [J]. Procedia computer science，2018，131：6?14. [18] ZHANG Weidong，DONG Lili，PAN Xipeng，et al. Singleimage defogging based on multi ? channel convolutionalMSRCR [J]. IEEE access，2019，7（1）：72492?72504. [19] 衡寶川，肖迪，張翔 . 結合 MSRCP 增強的夜間彩色圖像拼接算法[J].計算機工程與設計，2019，40（11）：3200?3204. [20] LI Mading，LIU Jiaying，YANG Wenhua，et al. Structure ?revealing low ? light image enhancement via robust Retinexmodel [J]. IEEE transactions on image processing， 2018（99）：2828?2841. [21] ZOTIN Alexander. Fast algorithm of image enhancementbased on multi ? scale Retinex [J]. Procedia computer science，2018，131：6?14. [22] 王衛星，肖翔，陳良琴 .結合最小濾波和引導濾波的暗原色去霧[J].光學精密工程，2015，23（7）：2100?2108. [23] KUMAR M，RNAN A. Image enhancement using contrastlimited adaptive histogram equalization and wiener filter [J].International journal of advanced trends in computer scienceand engineering，2016（2）：11?19. [24] 盛驟 . 概率論與數理統計[M].3 版 . 北京：高等教育出版社，2001. [25] RAJU G， NAIR M S. A fast and efficient color imageenhancement method based on fuzzy ? logic and histogram [J].AEUe ?international journal of electronices and communications，2014，68（3）：237?243. [26] 孫星星，鄭俊褒，曹志玲 .基于引導濾波與 LoG 算子的安檢圖像增強算法[J].軟件導刊，2020，19（8）：226?229.

作者簡介：

王利娟（1994—），女，山西大同人，在讀碩士研究生，主要研究方向為數字圖像處理。

常??霞（1982—），女，寧夏石嘴山人，博士，副教授，主要研究方向為智能信息處理。

張伯妍（1996—），女，山西呂梁人，在讀碩士研究生，主要研究方向為數字圖像處理。

編輯：黃飛

?