二級倒立擺的模糊控制研究
1 引言
??? 在控制理論發展的過程中,某一理論的正確性及實際應用中的可行性都需要一個按其理論設計的控制器控制一個典型對象進行驗證。倒立擺就是這樣一個被控制對象。倒立擺系統是一個多變量、快速、非線性和自然不穩定系統,在控制過程中該系統能有效反映控制中的許多關鍵問題,如非線性問題、系統的魯棒性問題、隨動問題、鎮定問題及跟蹤問題等。倒立擺在控制理論研究中是一種較為理想的實驗裝置。小車倒立擺系統的控制目標是倒立擺通過小車能夠穩定在有限長度的導軌上而不倒下,從而達到動態平衡。本文針對二級倒立擺非線性模型,基于Maminadi模型,通過設計融合函數來設計模糊控制器,有效解決規則爆炸問題,實現二級倒立擺的有效控制。
2 二級倒立擺的數學模型的建立
??? 二級倒立擺由小車、擺桿、水平導軌等組成,小車由伺服電機、皮帶輪、傳動帶帶動在水平導軌上左右運動,上下擺可繞各自的轉軸在水平導軌所在的鉛垂面內自由轉動。小車和上下擺桿間通過軸承連接,每個軸承連接處固定有電位器,分別用以檢測兩根擺桿與鉛垂線的角度偏移。小車相對軌道中心點的偏移位置也由固定在皮帶輪軸上的電位器檢測。
??? 其基本原理為:角度、位置信號經檢測電路獲取后,再由微分電路得到相應的微分信號,這些信號經A/D轉換器轉換為數字信號傳輸至計算機。通過已設計的控制程序計算控制力所需電壓值,經D/A轉換器轉換為模擬信號,功率放大后驅動電機運轉,電機再用皮帶拖動小車在導軌上往復運動實現對倒立擺的有效控制。忽略空氣阻力和各種摩擦,并認為擺桿為剛體。圖1為二級倒立擺示意圖。
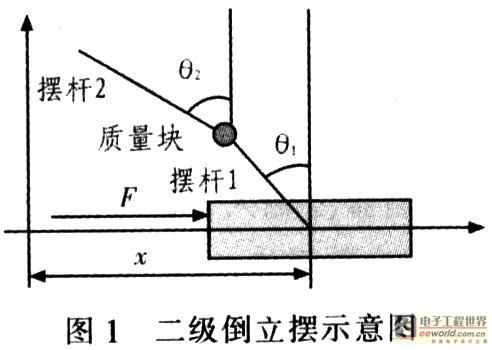
??? 倒立擺參數定義如下:M為小車質量,0.584 kg;m1為擺桿1質量,0.05 kg;m2為擺桿2質量,0.13 kg;m3為擺桿3質量,0.236 kg;l1為擺桿1中心到轉動中心的距離,0.077 5 m;l2為擺桿2中心到轉動中心的距離,0.25 m;θ1為擺桿1與豎直方向的夾角;θ2為擺桿2與豎直方向的夾角;F為作用在系統上的外力;g為重力加速度,9.8 m/s2。
??? 利用拉格朗日方程推導運動學方程,拉格朗日方程為:
??? ![]()
式中,L為拉格朗日算子,q為系統的廣義坐標,T為系統的動能,V為系統的勢能。
??? 
式中,i=1,2,3…,n,fi為系統在第i個廣義坐標上的外力。
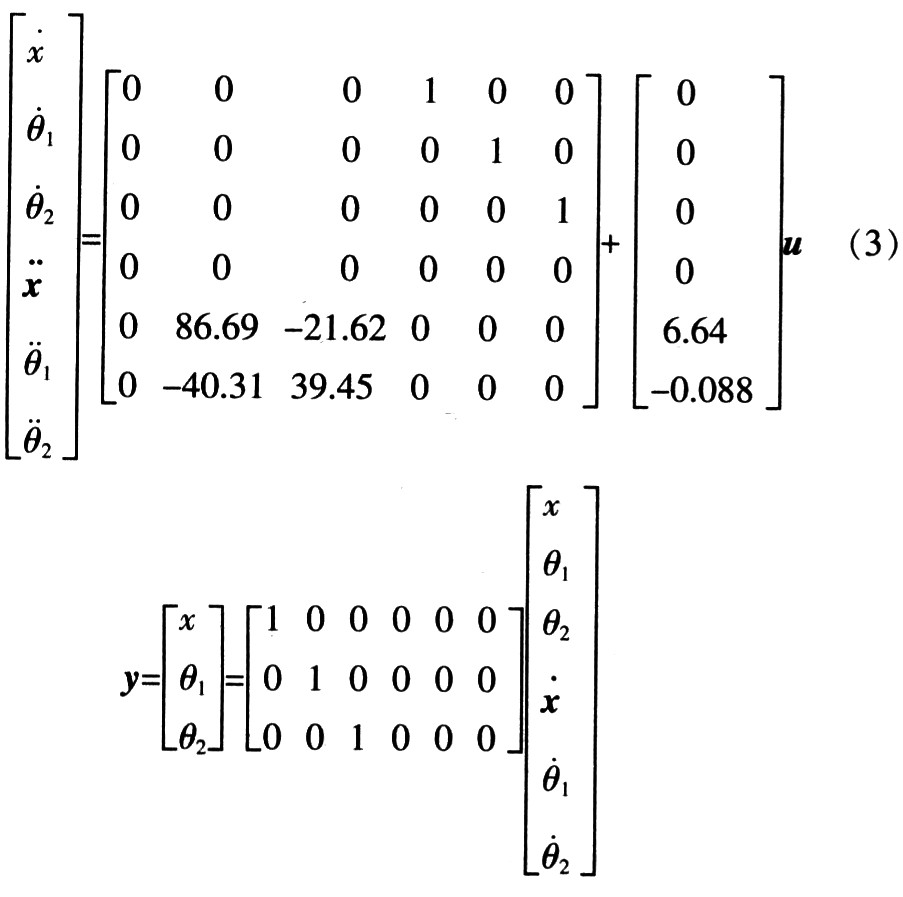
??? 在二級倒立擺系統中,系統的廣義坐標有3個,分別為x,θ1,θ2。經計算并線性化并帶人參數值得到系統的狀態空間方程:
??? 
??? 二級倒立擺系統控制目標較多,包括小車位移,下擺擺角,上擺擺角。傳統的模糊控制器采用系統誤差,誤差的導數作為輸入,若用傳統模糊控制控制二級倒立擺,則模糊控制器有6個輸入:小車位移、小車速度、下擺擺角、下擺角速度、上擺擺角和上擺角速度。
??? 若對每個輸入變量定義5個模糊子集,控制規則最多有56個,模糊控制規則設計復雜,可調參數非常多,不利于模糊規則的完整制定,這就是在使用模糊控制研究多變量非線性系統時的所謂“規則爆炸(Rule Explosion)”問題。然而,如果用3組二維模糊控制器(2輸入1輸出)通過串行或并行設計控制器,由于控制器個數增加,大大降低控制實時性,甚至由于不能及時輸出當前控制作用力而失控。
3.1 倒立擺控制合成變量
??? 本文是將最優控制理論與模糊控制相結合而采用的一種融合技術。它是把小車的位移、上擺擺角、下擺擺角綜合成一個變量E,將小車的速度、上擺的角速度、下擺的角速度綜合成一個變量EC,E和EC作為模糊控制器的輸入,電壓u作為輸出,減少模糊控制器的輸入,解決規則爆炸的問題,由此設計Mamdani型模糊控制器。
??? 通過LQR仿真,得出輸入輸出數據對,根據得到的數據計算并制定模糊規則。
??? 對于嵌套函數Y=f2[f1(x)],先使f1(x)對輸入變量作初步處理,再利用算法f2(x)根據前級算法的輸出進行控制。f1稱為融合函數,f2稱為作用函數。
??? 首先利用最優控制理論中的LQR求得系統的狀態反饋系數K和狀態向量x:
??? ![]()
??? 為實現變量融合,分別選取兩個反饋系數為控制主元,其他輸入變量可根據與主元的相關性和可融合性分別歸并到兩主元中。對于二級倒立擺,由于擺桿2的控制難度最大,分別選擇θ2、θ2為控制主元,相應系數為:kθ=kθ2,kθ=kθ2融合函數的輸出向量為: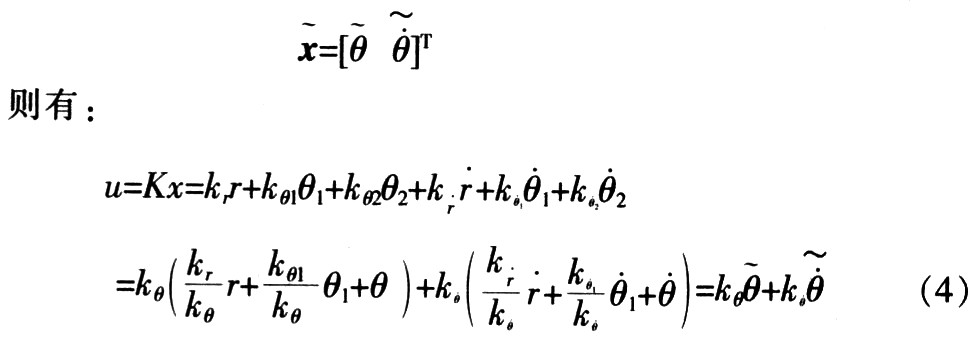
??? 融合函數的輸出方程為:
??? 
??? 通過把輸入狀態變量降維,得到角度誤差E和角速度誤差EC:
??? 
??? 通過信息融合,將系統的6個狀態變量化為2個狀態變量,減少系統的輸入,實現模糊控制器的降維。由降維后得到的2個變量E和EC做為模糊控制器的輸入,設計一個二維Mamdani型的模糊控制器。利用最優控制求得K。最優控制性能指標函數為:
??? 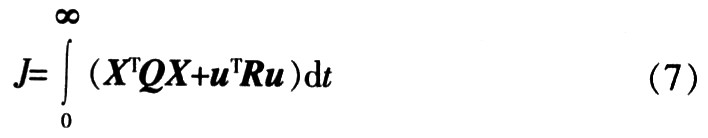
??? 使式(7)為最小,可求得:
??? ![]()
??? 求解如下Ricatti方程可得到矩陣P:
??? ![]()
??? 性能指標函數中,定義矩陣Q和矩陣R用來平衡系統對輸入量和狀態量的敏感程度。它們對閉環系統的動態性能影響很大。
??? 在倒立擺系統中,Q,R分別用來對狀態向量x和輸入控制量u進行平衡加權。一般情況下,P增加時,控制力減小,角度變化變小,跟隨速度變慢。而Q中某元素增加時,其對應的狀態變量的響應速度也增加,其他狀態變量的響應速度相對減慢。為了使得反饋矩陣K更合理,對矩陣Q,R的選取一定要盡量恰當。通過反復測試,實際系統的控制過程選取Q=diag[500 700 700 0 0 0],R=1。
??? 根據二級倒立擺的參數,基于MATLAB強大的矩陣運算及其豐富的內部函數,利用K=lqr(A,B,Q,R)命令計算,可得到狀態反饋矩陣K:
??? ![]()
??? 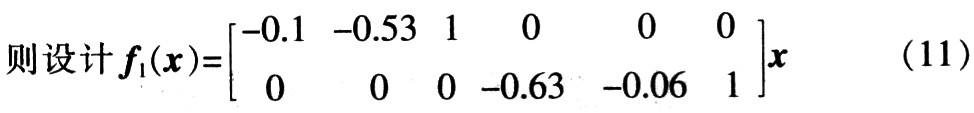
??? 從而得到綜合誤差E和綜合誤差變化率EC。
3.2 降維后設計二維Mamdani型模糊控制器
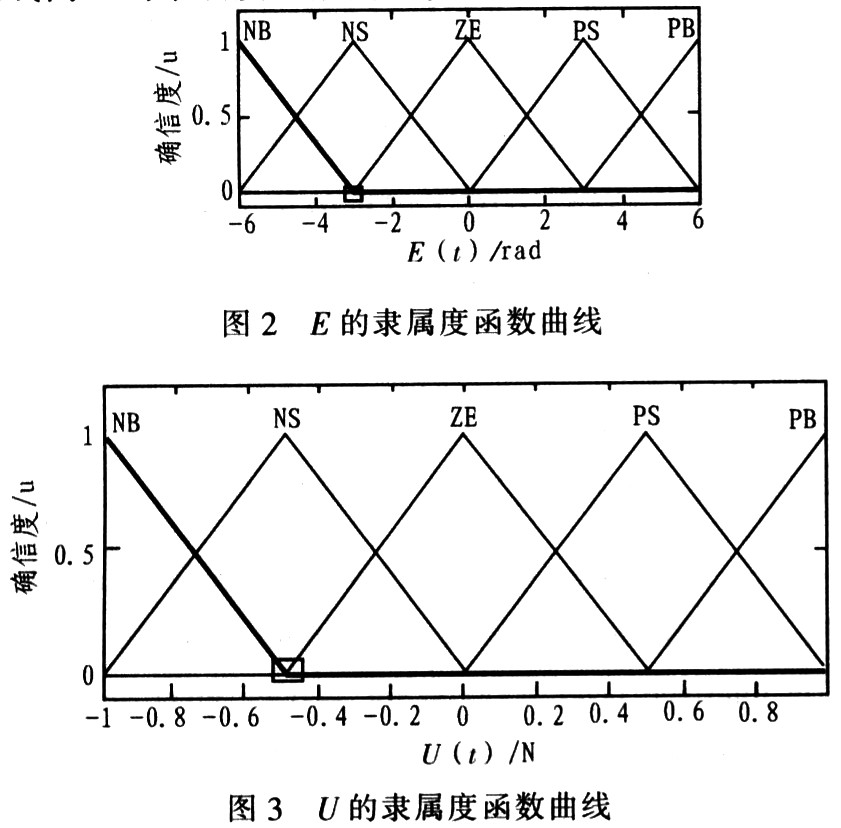
??? 輸入變量E、EC,輸出變量u;E、EC論域設定:E=[-6,6],EC=[-6,6],輸出論域U=[-1,1]均采用三角型、全交迭、均勻分布隸屬度函數。每個變量用5個模糊子集{NB NS ZE PS PB}來描述,隸屬度函數曲線圖如圖2、圖3所示。EC的隸屬度函數曲線同E的隸屬度函數曲線。
??? 模糊推理采用Mamdani最小運算規則。根據輸入、輸出論域上的模糊語言變量劃分NB(負大),NS(負小),ZE(零),PS(正小),PB(正大),設計模糊推理規則如圖4所示。
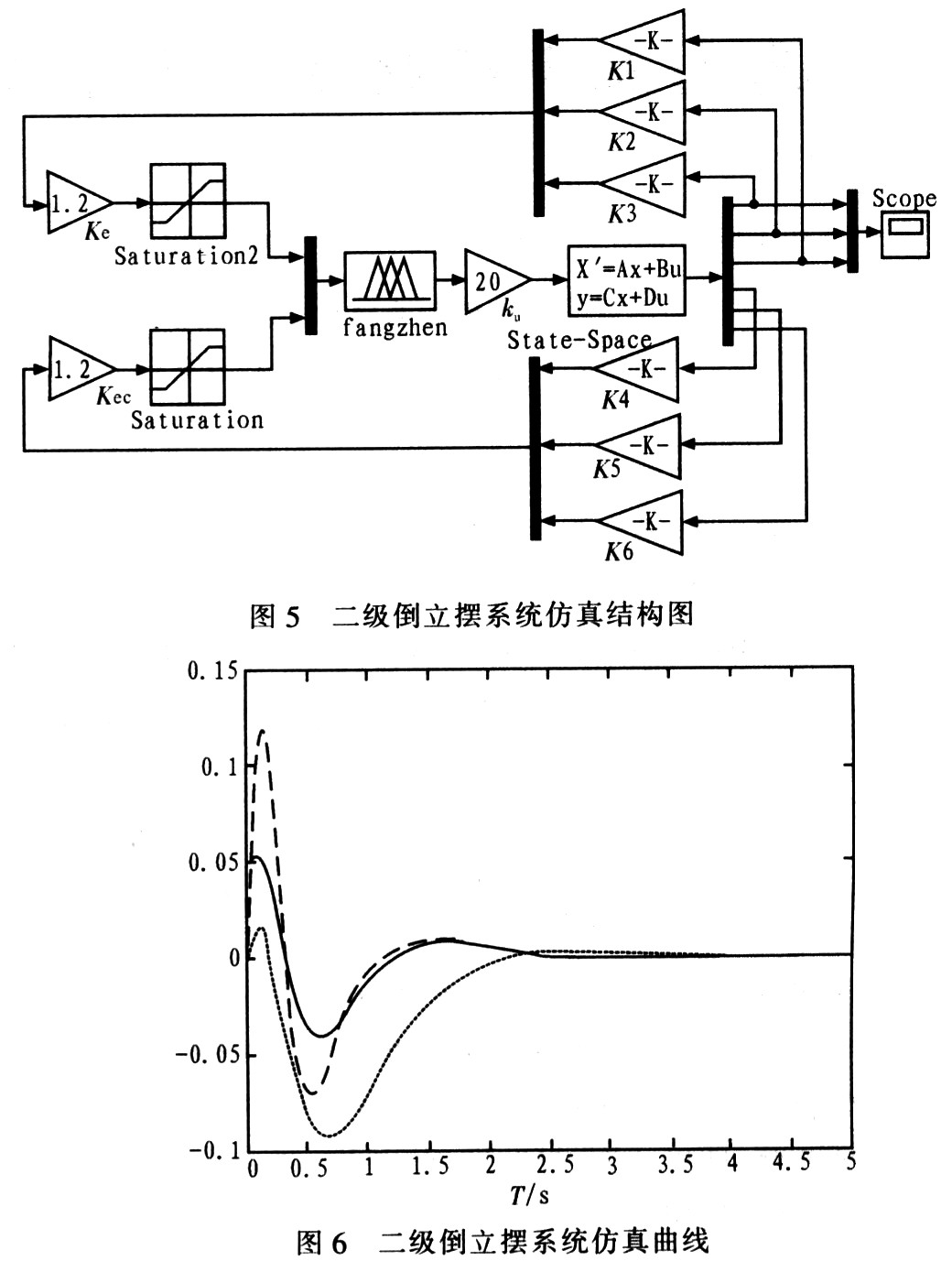
??? 模糊控制器采用重心法實現非模糊化,與一般采用的最大隸屬度法相比較,重心法具有更加平滑的輸出推理控制。通過以上分析和試驗,并恰當地選擇模糊邏輯系統的參數,從而設計一個適合被控對象的模糊控制器,如圖5所示。圖5中,Ke、Kec為量化因子,Ku為比例因子,State-Space為系統的狀態空間方程,Saturation為限幅模塊,Scope為示波器模塊。根據以上工作,在Simulink環境中對二級倒立擺系統進行仿真,其仿真曲線如圖6所示。
4 結束語
??? 二級倒立擺是典型的多輸入、非線性、強耦合系統。通過設計融合函數降低控制器的輸入維數,用模糊控制解決多輸入系統時遇到的模糊規則爆炸問題,使設計的實用模糊控制器成為可能。融合函數的設計方法還可推廣應用到一級、三級倒立擺系統中。該模糊控制器設計切實可行,能較好地控制系統,達到較好的控制效果。模糊控制具有魯棒性和穩定性好、算法簡單等特點,應用在實時性要求較高的場合,該控制方法也可應用到其他多變量、非線性系統的控制問題。
 電子發燒友App
電子發燒友App






















評論