量子密碼技術,量子密碼技術原理解析

在今天的信息時代,大量的敏感信息如病歷、法庭記錄、資金轉移、私人財產等常常通過公共通信設施或計算機網絡來進行交換,而這些信息的秘密性和真實性是人們迫切需要的.密碼學經過傳統的秘密密鑰加密體制、公共密鑰加密體制長期的演繹和發展,各種理論和算法推陳出新,極大推動了網絡信息一體化的蓬勃發展.然而,當理性地看待今天網絡安全技術的現狀和展望其未來的發展趨勢時,不得不更多地從總體和長遠性來思考一直困擾著密碼設計者的系統體制問題.

圖1所示典型加密系統是通過密鑰K將明文P轉換成密文C,放在公共信道上發送,在接受方進行逆變換的解密恢復可讀明文.其安全性在于通信雙方首先能在安全信道上傳遞密鑰,一次一密鑰方案(注意:密鑰K長度應不小于明文P的長度,即熵H(K)≥H(P)).C.E.Shannon證明是絕對安全的.可是在幾乎所有應用系統里,這幾乎是不可能實現的,尤其致命的是:既然通信雙方要進行保密通信,他們首先必須獲得密鑰,即需要進行獲得密鑰的秘密通信,但這種安全性是得不到證明的,通信雙方對是否存在竊聽者毫無所知；這就是在保密通信中經常涉及到的“Catch 22”問題,原因在于密鑰的建立過程總要利用某種載體的某種物理屬性,而經典物理學指出,測量該載體的這些屬性對其不會產生任何影響.

圖1　典型通信加密系統

解決“Catch 22”問題一種方案是現代密碼學中的公鑰密碼體制(PKCS),如圖2所示.通信雙方可以建立各自的加密／解密密鑰對(Ek,Dk),將加密密鑰Ek公開同時,各自妥善保管專有解密密鑰Dk,這種加密體制的安全性大多建立在一些著名的數學難題基礎之上,通過設計單向陷門函數以實現加解密算法的不可逆性(至少在現有的資源和算法下是不現實的).從理論上說,由公開密鑰獲得秘密密鑰在計算上是不可能的,“Catch 22”問題似乎得到了解決,但到目前為止還沒有人能證明是否存在真正的單向陷門函數,因此也就沒有人真正了解公鑰密碼體制的安全強度.從根本上說,公鑰體制是在一定程度上繞過了“Catch 22”問題,隨著數學和計算技術的快速發展,特別是最近發展的量子計算技術,當量子計算機成為現實時,公鑰密碼體制將可以很容易地被破譯,例如應用肖氏(Shor's)量子分解因式算法可以在多項式時間內輕易地破解RSA加密算法.另一個缺陷是眾多實際應用中的公鑰密碼系統,其密鑰往往由密鑰管理中心獨立管理,因此在收發方進行保密通信之前仍然需要通過秘密信道與管理中心通信.基于此,公鑰體制沒有徹底解決“Catch 22”問題.而量子密碼體制提供了可證明的安全性和對外界干擾的檢測性［1］,從而解決了“Catch 22”這個一直未能解決的重要問題.

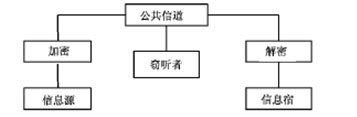
圖2　公開密鑰加密體系

現代密碼學認為,任何加密體系的加、解密算法都是可以公開的,其安全性應該在于密鑰的保密性.量子密碼方案在密鑰分配協議中提供了傳統密碼體制所無法比擬的潛在優勢:具有可證明的安全性；能在密鑰生成之前進行量子通信以檢測侵入者的威脅,為此它為未來的保密通信提供了最終確實的保障.以下在涉及正題之前先作一個大致的描述:

首先通信發送者隨機選擇一二進制序列,序列中的每一比特都由隨機選擇的具有某量子態(例如偏振態)的單光子代表,從而在真正物理意義上是發送一串特定時間間隔的單光子序列,接收方則保持同步地隨機選擇探測方法,獨立地探測光脈沖中各單光子狀態,如果探測到了一個光子,他就記錄下探測到它的時間、結果、方法；發送接收完畢后,雙方在公共信道里討論光子序列的總體接收情況,接收方告訴發送方他接收到各光子的時間和探測方法,但不通報結果；發送方根據自己的發送記錄與反饋信息,通知接收方哪些光子的接收方法是正確的,摒棄那些未被接收到的光子和探測方法錯誤的光子,接收方根據提示從所收到的初始光子序列中提取有用的比特,建立起初始密鑰(Raw key)；而后通信雙方再任意從初始密鑰中選取一部分,逐個比較比特值,判斷誤碼率是否超出了誤差閾值(藉此推斷竊聽者是否存在),在未超出情況下去除初始密鑰測試部分,余下的比特序列再經過一定的誤差校驗算法構成正式通信密鑰,否則放棄所有數據,檢查通道,重頭開始通信.

量子密碼理論

量子物理與經典物理最重要的區別可以概括為互補性和相關性.常說的波粒二象形就是一個量子體系的兩種互補屬性,在著名的楊氏雙縫實驗中,如果想確知發出的某光子通過哪個縫隙,因而來探測系統的微粒性,結果將導致無法觀測到光的干涉現象；同樣,如果想觀測光的干涉現象,所以測量系統的波動性時,就無法確定光子通過的路徑.量子密碼技術正是應用了這一互補性以及量子力學的基本理論［2,3］,包括海森伯格測不準原理和單光子的不可分割性,從而解決了經典密碼學一直無法妥善處理的安全性問題,表述如下:

設A和B分別是表示一個量子體系兩力學量的算符,二者不對易,即 [A,B］=AB-BA≠0,　　(1) 這意味著,A和B不能同時有確定值,在同一個態ψ中,A和B不確定程度滿足下列關系: <(ΔA)2〉〈(ΔB)2≥1/4‖〈［A,B］〉‖2,　　(2) 注:ΔA=A-〈A〉; ΔB=B-〈B〉;

<(ΔA)2〉代表算符A的均方偏差;〈(ΔB)2〉代表算符B的均方偏差. 海森伯格測不準原理說明,微觀粒子兩類非相容可觀測態的屬性是互補的,對其中一種屬性的精確測量必然會導致其互補屬性的不確定性.在量子力學中,一個物質體系(例如一個電子或一個光子)是用希耳伯特空間中的一個態矢量來表示,體系的每種物理屬性(例如坐標或動量)均用專有算符表示,而每個算符的所有本征態(組成完全系)構成希耳伯特空間中一組相互正交的基態(基矢),任何態矢量都可以按照一個完全系的基矢進行展開,例如:態矢量|ψ〉,按照算符A的本征態展開如下:

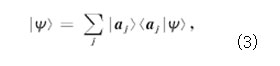
注:aj是算符A在各本征態的本征值,滿足方程A|aj〉=aj|aj〉,式(3)說明,對算符A進行數值測量,測量結果為aj,同時使被測量體系處于新的態矢量|aj〉的概率為‖〈aj|ψ〉‖2.具體說,就是在量子通信中,竊聽者對傳送的光子序列所進行的任何干擾、竊聽,例如量子拷貝、截取/重發等,都將導致光子狀態的改變,從而影響接收者的測量結果,由此可對竊聽者的行為進行判定和檢測.現在假設如圖3.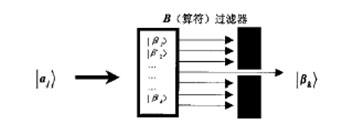

圖3　正常量子信道發-收模型

態矢量|aj〉入射到B(算符)過濾器上,只允許其本征態|βk〉(滿足B|βk〉=βk|βk〉) 通過,根據展開式:測量的本征值為βk的概率為‖〈βk|aj〉‖2.如果態矢量|aj〉按照另一個算符E的本征態進行展開:假若態矢量|aj〉在入射到B(算符)過濾器之前,被插入E(算符)過濾器,見圖4.那么此系統最終測得本征值為βk的所有可能的概率總計為

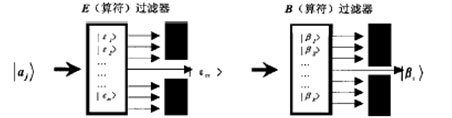
圖4　存在竊聽者的量子信道模型

通過比較式(4)和(5),可以得出:

用雙縫試驗進行類比來形象說明的話,E(算符)過濾器就相當于檢測光子的精確軌跡,式(5)是代表波動性的干涉現象遭到破壞后的結果數學表達式.那么能鑒別出中途是否進行過測量嗎？可以.因為無法鑒別就是要式(5)和(6)相等,這必須滿足:

因此只要算符A和B本身是相容的可觀測態,而E與A、B不對易(屬性互補),通過對B(算符)過濾裝置輸出結果進行數理統計,就能檢測出是否應用過E(算符)過濾器進行了干擾.以下重點介紹量子密鑰分發協議,深入了解一下實際運作的量子密碼術。