我們在許多介紹零知識證明的文章中都能看到這樣三個性質：

Completeness —— 完備性

Soundness —— 可靠性

Zero-Knowledge —— 零知識

但是少有文章深入解釋這個特性背后的深意和洞見。

通常，我們定義安全會采用這樣一種方式，首先列出一些安全事件，然后說明：如果一個系統安全，那么列出來的安全事件都不會發生。

借用密碼學家 Boaz Barak 的話，翻譯一下，「零知識證明」并不是通過給出一個不允許發生的事件列表來定義，而是直接給出了一個最極致的「模擬條件」。

所謂「模擬條件」是指，通過「模擬」方法來實現一個「理想世界」，使之與「現實世界」不可區分；而由于在理想世界中不存在知識，所以可以推導出結論：現實世界滿足「零知識」。

我們繼續分析下一個交互系統（安全協議）的三個性質：「完備性」、「可靠性」與「零知識」。

· 可靠性（Soundness）：Alice 在沒有知識的情況下不能通過 Bob 的驗證。

· 完備性（Completeness）：Alice 在有知識的情況下可以通過 Bob 的驗證。

· 零知識（Zero-knowledge）：Alice 在交互的過程中不會泄露關于知識的任何信息。

我們可以看出來「可靠性」和「完備性」有一種「對稱性」。可靠性保證了惡意的 Alice 一定失敗，而完備性保證了誠實的 Alice 一定成功。

「完備性」比較容易證明，只要 Alice 誠實，Bob 也誠實，那么皆大歡喜。這好比，寫好一段代碼，喂了一個測試用例，跑完通過收工。

我們來想想「可靠性」應該如何定義？這個可靠性的逆否命題是：（在現實世界中）如果 Alice 能通過 Bob 的驗證，那么 Alice 一定有知識。或者說：Alice 知道那……個「秘密」！

下面的問題是如何證明 Alice 知道一個「秘密」？

這好像也很難，對不對？假如我們需要證明一臺機器知道一個「秘密」，最簡單的辦法就是我們在機器的硬盤里，或者內存中找到這個「秘密」，但是這樣暴露了秘密。如果這臺機器是黑盒子呢？或者是 Alice 呢？我們沒有讀心術，猜不到她心里的那個秘密。

如何定義「To Know」？

「零知識」保證了 驗證者 Bob 沒有（計算）能力來把和「知識」有關的信息「抽取」出來。不能抽取的「知識」不代表不存在。「可靠性」保證了知識的「存在性」。

只有「知識」在存在的前提下，保證「零知識」才有意義。

為了進一步分析「知識」，接下來首先介紹一個非常簡潔，用途廣泛的零知識證明系統 —— Schnorr 協議。這個協議代表了一大類的安全協議，所謂的 Σ-協議，而且 Schnorr 協議擴展也是『零知識數據交換協議 zkPoD』［1］ 的核心技術之一。

簡潔的 Schnorr 協議

Alice 擁有一個秘密數字，a，我們可以把這個數字想象成「私鑰」，然后把它「映射」到橢圓曲線群上的一個點 a*G，簡寫為 aG。這個點我們把它當做「公鑰」。

sk = a

PK = aG

請注意「映射」這個詞，我們這里先簡要介紹「同態」這個概念。橢圓曲線群有限域之間存在著一種同態映射關系。有限域，我們用 Zq 這個符號表示，其中素數 q是指有限域的大小，它是指從 0， 1， 2， …， q-1 這樣一個整數集合。而在一條橢圓曲線上，我們通過一個基點，G，可以產生一個「循環群」，標記為 0G， G， 2G， …， （q-1）G，正好是數量為 q 個 曲線點的集合。任意兩個曲線點正好可以進行一種「特殊的二元運算」，G + G = 2G，2G + 3G = 5G，看起來這個二元運算好像和「加法」類似，滿足交換律和結合律。于是我們就用 +這個符號來表示。之所以把這個群稱為循環群，因為把群的最后一個元素 （q-1）G，再加上一個 G就回卷到群的第一個元素 0G。

給任意一個有限域上的整數 r，我們就可以在循環群中找到一個對應的點 rG，或者用一個標量乘法來表示 r*G。但是反過來計算是很「困難」的，這是一個「密碼學難題」—— 被稱為離散對數難題［2］。

也就是說，如果任意給一個橢圓曲線循環群上的點 R，那么到底是有限域中的哪一個整數對應 R，這個計算是很難的，如果有限域足夠大，比如說 256bit 這么大，我們姑且可以認為這個反向計算是不可能做到的。

Schnorr 協議充分利用了有限域和循環群之間單向映射，實現了最簡單的零知識證明安全協議：Alice 向 Bob 證明她擁有 PK 對應的私鑰 sk。

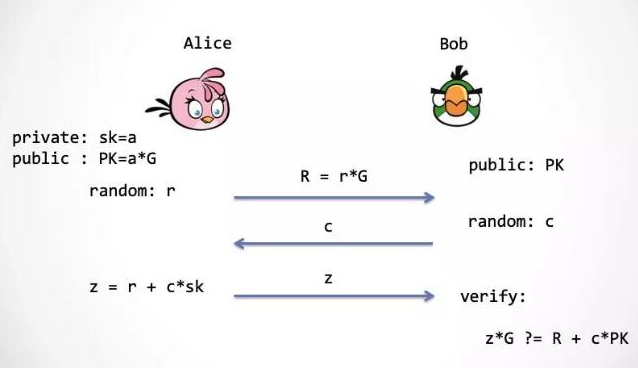
第一步：為了保證零知識，Alice 需要先產生一個隨機數，r，這個隨機數的用途是用來保護私鑰無法被 Bob 抽取出來。這個隨機數也需要映射到橢圓曲線群上，rG。

第二步：Bob 要提供一個隨機數進行挑戰，我們把它稱為 c。

第三步：Alice 根據挑戰數計算 z = r + a * c，同時把 z發給 Bob，Bob通過下面的式子進行檢驗：z*G ？= R + c*PK = rG + c*（aG）

大家可以看到 Bob 在第三步「同態地」檢驗 z 的計算過程。如果這個式子成立，那么就能證明 Alice 確實有私鑰 a。

可是，這是為什么呢？

z 的計算和驗證過程很有趣，有幾個關鍵技巧：

1. 首先 Bob 必須給出一個「隨機」挑戰數，然后 Bob 在橢圓曲線上同態地檢查 z 。如果我們把挑戰數 c 看成是一個未知數，那么 r+a*c=z 可以看成是一個一元一次方程，其中 r 與 a 是方程系數。請注意在 c 未知的前提下，如果 r + a*x = r‘ + a’*x 要成立，那么根據 Schwatz-Zippel 定理［3］，極大概率上 r=r‘，a=a’ 都成立。也就是說， Alice 在 c 未知的前提下，想找到另一對不同的 r‘，a’ 來計算 z 騙過 Bob 是幾乎不可能的。這個隨機挑戰數 c 實現了r 和 a 的限制。雖然 Bob 隨機選了一個數，但是由于 Alice 事先不知道，所以 Alice 不得不使用私鑰 a 來計算 z。這里的關鍵： c 必須是個隨機數。

2. Bob 驗證是在橢圓曲線群上完成。Bob 不知道r，但是他知道 r 映射到曲線上的點R；Bob 也不知道 a，但是他知道 a 映射到曲線群上的點 PK，即 a*G。通過同態映射與Schwatz-Zippel 定理，Bob 可以校驗 z 的計算過程是否正確，從而知道 Alice 確實是通過 r 和 a 計算得出的 z，但是又不暴露 r 與 a 的值。

3. 還有，在協議第一步中產生的隨機數 r 保證了 a 的保密性。因為任何一個秘密當和一個符合「一致性分布」的隨機數相加之后的和仍然符合「一致性分布」。

證明零知識

我們這里看一下 Schnorr 協議如何證明一個弱一些的「零知識」性質——「SHVZK」：

注：這里我們證明的僅僅是 Special Honest Verifier Zero-Knowledge（SHVZK）。SHVZK 要求協議中的 Bob 的行為不能不按常理出牌，比如他必須按協議約定，在第二步時，去傳送帶上取一個新鮮的隨機數，并且立即使用。而通常意義上的「零知識」是不會對 Bob 做任何要求，所以我們說這里是一個弱一些的性質。雖然目前 Schnorr 協議不能證明完全的「零知識」，但經過添加一些協議步驟，就可以達到完全零知識的目的，細節這里不展開，有興趣的讀者請參考文獻［4］。以后我們在討論 Fiat-Shamir 變換時，還會再次討論這個問題。

首先「模擬器」模擬一個「理想世界」，在理想世界中模擬出一個 Zlice 和 Bob 對話，Zlice 沒有 Schnorr 協議中的知識，sk，而 Bob 是有公鑰 PK的。請大家看下圖，Bob 需要在 Schnorr 協議中的第二步出示一個隨機數 c，這里有個額外的要求， 就是 Bob 只能「誠實地」從一個外部「隨機數傳送帶」上拿一個隨機數，每一個隨機數都必須是事先拋k次「硬幣」產生的一個 2^k 范圍內的一次性分布隨機數。Bob 不能采用任何別的方式產生隨機數，這就是為何我們要求 Bob 是誠實的。

下面演示 Zlice 如何騙過 Bob：

序幕：請注意 Zlice 沒有關于 sk 的知識，這時 Bob 的隨機數傳送帶上已經預先放置了一些隨機數。

第一步：Zlice 產生一個一致性分布的隨機數 c，并且利用一個新的「超能力」，將剛剛產生的隨機數 c 替換掉 Bob 的隨機數傳送帶上第一個隨機數。這時候，Bob 無法察覺。

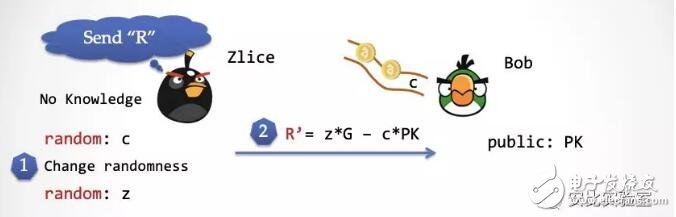
第二步：Zlice 再次產生一個隨機數 z，然后計算 R‘=z*G - c*PK，并將 R’ 發送給 Bob。

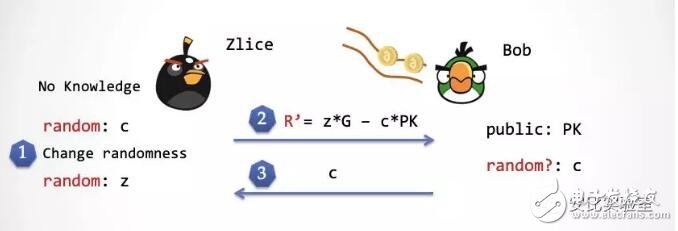
第三步：這時候Bob 會從隨機數傳送帶上取得 c，并且將 c 發送給 Zlice。請注意這個 c 正好就是第一步中 Zlice 產生的 c。

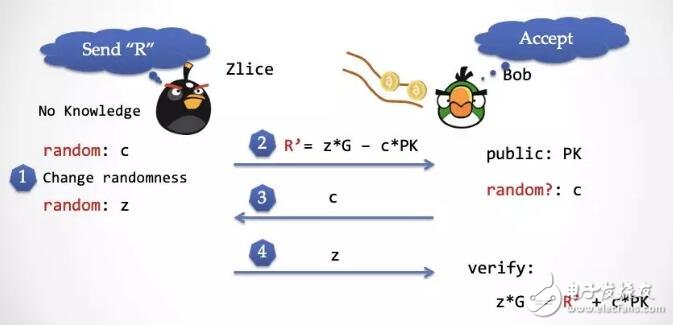
第四步：Zlice 將第三步產生的隨機數 z 發送給 Bob，Bob 按照 Schnorr 協議的驗證公式進行驗證，大家可以檢查下，這個公式完美成立。

大家可以再對比下「現實世界」的 Schnorr 協議，在兩個世界中，Bob 都能通過驗證。

但區別是：

· 在「理想世界中」，Zlice 沒有 sk；而在「現實世界中」，Alice 有 sk

· 在「理想世界中」，z 是一個隨機數，沒有涉及 sk；而在「現實世界中」，z 的計算過程里面包含 sk

· 在「理想世界中」，Zlice 使用了超能力，替換了 Bob 的隨機數；而在「現實世界中」，Alice 看不到 Bob 的隨機數傳送帶，也無法更改傳送帶上的數字

這里請大家思考下：

Schnorr 協議中，Bob 在第二步發挑戰數能不能和第一步對調順序？也就是說 Bob 能不能先發挑戰數，然后 Alice 再發送 R = r*G。

（兩分鐘后……）

答案是不能。

如果 Alice 能提前知道隨機數，那么 （現實世界中的）Alice 就可以按照模擬器 Zlice 做法來欺騙 Bob。

再遇模擬器

其實，「可靠性」和「零知識」這兩個性質在另一個維度上也是存在著一種對稱性。可靠性保證了惡意的 Alice 一定失敗，零知識保證了惡意的 Bob 一定不會成功。有趣地是，這種對稱性將體現在模擬出來的「理想世界」中。

我們分析下可靠性這個定義：Alice 沒有知識導致 Bob 驗證失敗。它的逆否命題為：Bob 驗證成功導致 Alice 一定有知識。

我們再次求助模擬器，讓他在可以發揮超能力的「理想世界」中，去檢驗 Alice 的知識。

再次，請大家設想在平行宇宙中，有兩個世界，一個是叫做「理想世界」，另一個叫做「現實世界」。理想世界有趣的地方在于它是被「模擬器」模擬出來的，同時模擬器可以在理想世界中放入帶有超能力的 NPC。這次把 Alice 的兩個分身同時放入「理想世界」與「現實世界」。

假設「你」扮演 Bob 的角色，你想知道和你對話的 Alice 是否真的是「可靠的」。于是把你放入「理想世界」，借助一個具有超能力的 NPC，你可以把對面的 Alice 的知識「抽取」出來。

W.。.hat？我們不是剛剛證明過：協議是零知識的嗎？零知識就意味著 Bob 抽取不出任何的「知識」碎片。這里敲黑板，「零知識」是對于「現實世界」而言的。我們現在正在討論的是神奇的「理想世界」。

重復一遍，在「理想世界」中，你可以借助一個有超能力的 NPC 來抽取 Alice 的知識，從而可以保證「現實世界」中的 Alice 無法作弊。可以想象一下，一個作弊的 Alice，她肯定沒有知識，沒有知識也就不可能在「理想世界」中讓 NPC 抽取到任何東西。

然而在「現實世界」中，你無法借助 NPC，當然也就看不到 Alice 的知識，也就不會和「零知識」性質沖突。因為兩個世界發生的事件是「不可區分」的，我們可以得到這樣的結論：在「現實世界」中，Alice 一定是存在知識的。

整理一下思路：如何證明在一個交互會話中 Alice 不能作弊呢？我們需要為這個交互會話定義一個「模擬算法」，該算法可以模擬出一個「理想世界」，其中有一個特殊的角色叫做「抽取器」（Extractor），也就是我們前面說的 NPC，它能夠通過「超能力」來「抽取」Alice 的知識，但是讓對方「無所察覺」。

注意，超能力是必不可少的！這一點在『系列（二）理解「模擬」』有解釋，如果模擬器在沒有超能力的情況下具備作弊能力，那相當于證明了協議「不可靠」（Unsoudness）。同樣地，如果「抽取器」在沒有超能力的情況下具備抽取信息能力，那相當于證明了協議不零知（Not-zero-knowledge）。

最后一點，超能力是什么？

這個要取決于具體的交互系統的證明，我們接下來就先拿我們剛剛講過的Schnorr 協議切入。

Proof of Knowledge ：「知識證明」

我們來證明一下 Schnorr 協議的「可靠性」，看看這個超能力 NPC 如何在「理想世界」中把 Alice 私鑰抽取出來。而這個「超能力」，仍然是「時間倒流」。

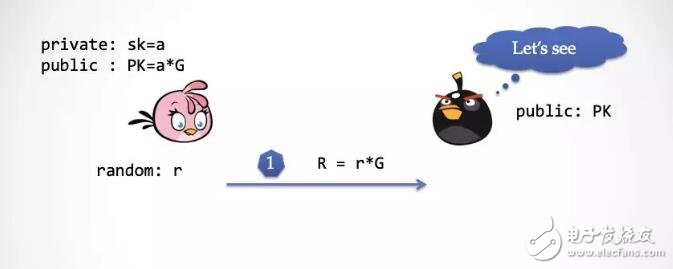
第一步：Alice 選擇一個隨機數 r，并且計算 R=r*G，并將 R 發給「抽取器」

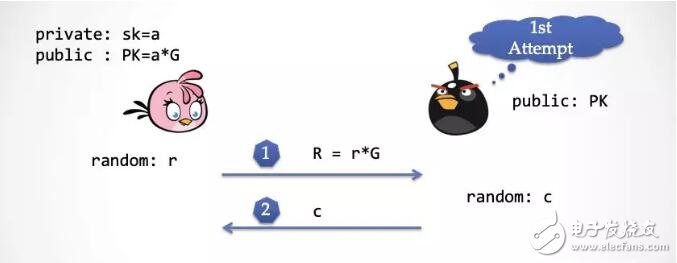
第二步：抽取器也選擇一個隨機的挑戰數c，并且發給 Alice

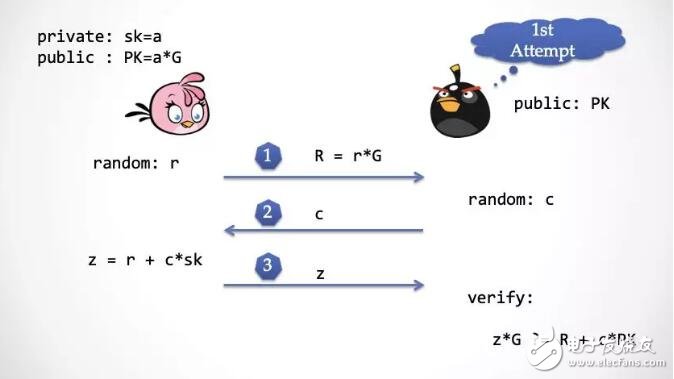
第三步：Alice 計算并且回應 z，然后抽取器檢查 z是否正確

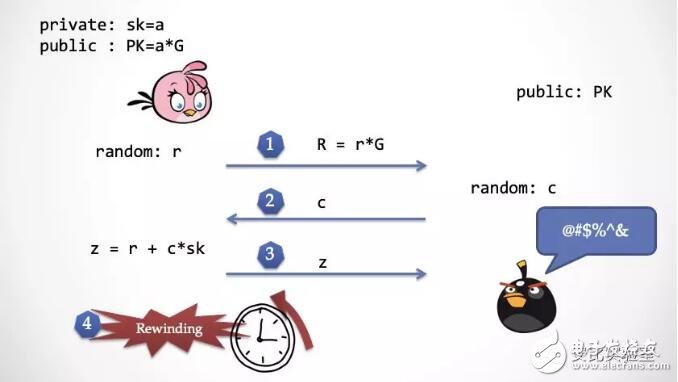
第四步：抽取器發現 z 沒有問題之后，發動超能力，將時間倒回第二步之前

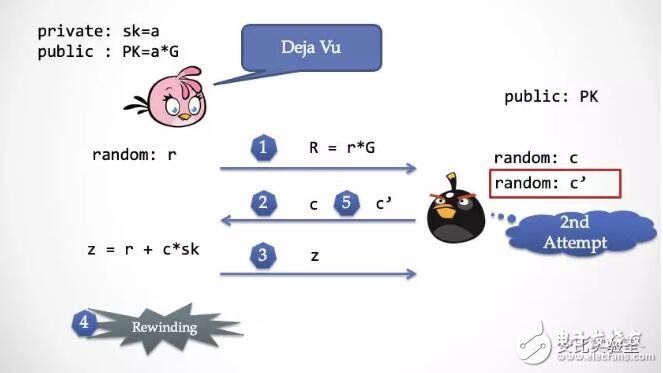
第五步：抽取器再次發送一個不同的隨機挑戰數 c‘給 Alice，這時候 Alice 回到第二步，會有一種似曾相識的感覺，但是無法感知到時間倒回這個事實

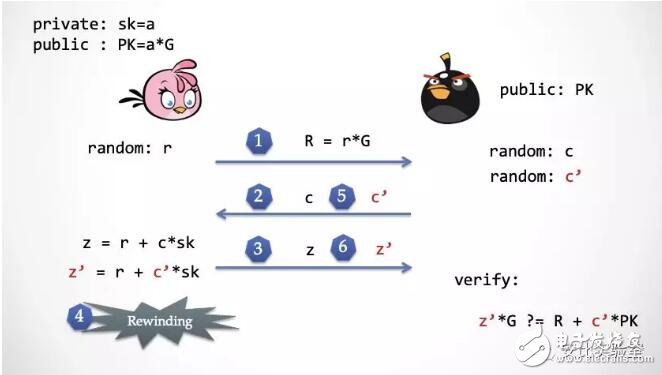
第六步：Alice 再次計算了 z’，然后發給抽取器檢查

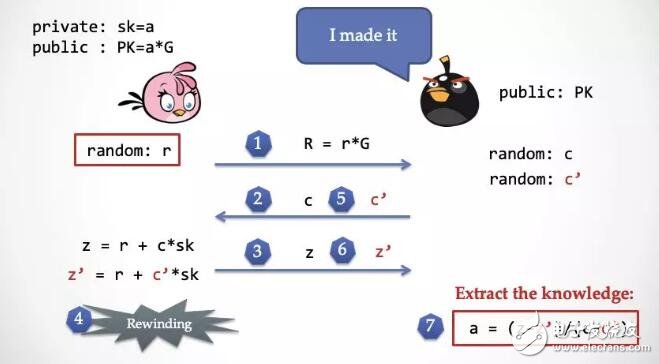
第七步：這時候抽取器有了z 和 z‘，就可以直接推算出 Alice 所擁有的私鑰 a，達成「知識抽取」

到這里，「可靠性」就基本證明完了。大家是不是對可靠性和零知性的「對稱性」有點感覺了？

總結一下：「抽取器」在「理想世界」中，通過時間倒流的超能力，把 Alice 的「知識」完整地「抽取」出來，這就保證了一個沒有知識的 Alice 是無法讓抽取器達成目標，從而證明了「可靠性」。

注：并不是所有的可靠性都必須要求存在抽取器算法。采用抽取器來證明可靠性的證明系統被稱為「Proof of Knowledge」。

解讀 ECDSA 簽名攻擊

在區塊鏈系統中到處可見的ECDSA 簽名方案也是一個樸素的零知識證明系統。橢圓曲線數字簽名方案 ECDSA 與 Schnorr 協議非常接近，基于 Schnorr 協議的簽名方案發表在 1991年的『密碼學雜志』［5］上。1991年，正值美國國家標準局（NIST）選擇數字簽名算法，優雅的 Schnorr 簽名方案居然被申請了專利，因此 NIST 提出了另一套簽名方案 DSA（Digital Signature Algorithm），隨后這個方案支持了橢圓曲線，于是被稱為 ECDSA。中本聰在構思比特幣時，選擇了 ECDSA 作為簽名算法，但是曲線并沒有選擇 NIST 標準推薦的橢圓曲線 —— secp256-r1，而是 secp256-k1。因為江湖傳言，NIST 可能在橢圓曲線參數選擇上做了手腳，導致某些機構可以用不為人知的辦法求解離散對數難題，從而有能力在「現實世界」中具備超能力。有不少人在懷疑，也許當年中本聰在設計比特幣時，也有這種考慮，故意選擇了 secp256-k1 這樣一條貌似安全性稍弱的曲線。

我們拆解下 ECDSA 簽名，用交互的方式定義一個類似 ECDSA 的認證方案，交互見下圖。

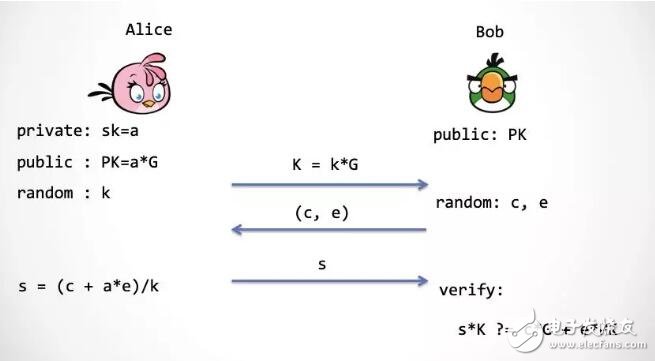
第一步：Alice 仍然是選擇一個隨機數 k，并將 k 映射到橢圓曲線上，得到點 K ，然后發送給 Bob

第二步：Bob 需要產生兩個隨機數，c 和 e，然后交給 Alice

第三步：Alice 計算 s，并且發送給 Bob，他來驗證 s 的計算過程是否正確

注：對熟悉 ECDSA 簽名方案的讀者，這里略作解釋，Bob 產生的 c 對應被簽消息的 Hash 值 Hash（m），而 e 則是由一個轉換函數 F（K）來產生。其中 F（。） 是取橢圓曲線上的點的 x 坐標經過 （mod q） 得到［6］。

江湖上流傳著一個說法：ECDSA 簽名方案有個嚴重的安全隱患，如果在兩次簽名中使用了同一個隨機數，那么簽名者的私鑰將會暴露出來。其實 Schnorr 簽名方案也有同樣的問題。

當年 Sony PlayStation 3 的工程師在調用 ECDSA 庫函數時，本來應該輸入隨機數的參數位置上，卻傳入了一個常數。熟悉密碼學的黑客們發現了這個嚴重的后門。2011年1月，神奇小子 Geohot 公開發布了 Sony PS3 的主私鑰，這意味著任何用戶都可以輕松拿到游戲機的 root 權限。Sony 隨后大為光火…… （后續故事大家可以上網搜）

如果 Alice 在兩次交互過程中使用了同一個 K，那么 Bob 可以通過發送兩個不同的 c 和 c’ 來得到 s 和 s‘，然后通過下面的公式算出私鑰 a：

k = （c - c’）/（s - s‘）

a = （k * s - c）/e

那么我們應該怎么來看這個「安全后門」呢？大家想想看，這個安全后門和我們前面證明過的 Schnorr 協議的可靠性證明幾乎一模一樣！這個算法正是 ECDSA 認證協議的「可靠性」證明中的「抽取器」算法。只不過在可靠性證明中，為了讓 Alice 使用同一個隨機數 k 來認證兩次，「抽取器」需要利用「時間倒流」的超能力。

但是在 Sony PS3 系統中，隨機數被不明所以的工程師寫成了一個固定不變的值，這樣相當于直接賦予了黑客「超能力」，而這是在「現實世界」中。或者說，黑客在不需要「時間倒流」的情況下就能實現「抽取器」。

提醒下，不僅僅是隨機數不能重復的問題。而是隨機數必須是具有密碼學安全強度的隨機數。

設想下，如果隨機數 r 是通過一個利用「線性同余」原理的偽隨機數生成器產生，雖然 r的值一直在變化，但是仍然不能阻止「知識抽取」。假設線性同余算法為 r2= d*r1 + e （mod m），還回到 Schnorr 協議的第三步：

1： z1 = r1 + c1*a

2： z2 = r2 + c2*a

如果攻擊者讓 Alice 連續做兩次簽名，那么將 r2 代入 r1 之后，就出現了兩個線性方程求解兩個未知數 （r1， a） 的情況，z1， z2， c1， c2， d， e 對于 攻擊者是已知的，這個方程組只用初中數學知識就可以求解。

請注意，這并不是 Schnorr 協議（或 ECDSA 協議）的「設計缺陷」，恰恰相反，這是 Schnorr 協議設計比較精巧的地方，它從原理上保證了協議的可靠性。類似技巧在密碼學協議中頻繁出現，達到一目了然的「簡潔」。但是也不得不說，如果不清楚協議的內在機制，尤其是區分不清楚「理想世界」與「現實世界」，使用者很容易引入各種花式的「安全漏洞」。

作為一個能寫出安全可靠軟件的負責任的碼農，我們需要了解哪些？徹底理解安全協議的設計機制當然是最好的，但是絕大多數情況下這是不現實的。一般來說，我們把各種密碼學工具當做「黑盒」來用，但這可能是不夠的，我們最好能了解下：

「安全定義」是什么？

「安全假設」到底是什么？

「理想世界」中的「超能力」到底是什么？

腦洞：我們生活在模擬世界中嗎

第一次讀懂「模擬器」時，我第一時間想到的是電影『黑客帝國』。我們生活所在「現實世界」也許是某一個模擬器模擬出來的「理想世界」，我們所看到、聽到的以及感知到的一切都是被「模擬」出來的。在「現實世界」里，我們活在一個母體中。然而我們并不能意識到這一點。

早在春秋戰國時期，莊子也在思考類似的問題：

昔者莊周夢為胡蝶，栩栩然胡蝶也。自喻適志與！不知周也。俄然覺，則蘧蘧然周也。不知周之夢為胡蝶與？胡蝶之夢為周與？周與胡蝶則必有分矣。此之謂物化。——《莊子·齊物論》

通俗地解釋下：莊子有一天睡著了，夢見自己變成了一只蝴蝶，翩翩起舞，醒來之后發現自己還是莊子，在夢中，蝴蝶并不知道自己是莊子。于是莊子沉思到底是他夢中變成了蝴蝶，還是蝴蝶夢中變成了莊子呢？如果夢境足夠真實，……

「缸中之腦」是美國哲學家 Gilbert Harman 提出的這樣一個想法：一個人的大腦可以被放入一個容器里面，然后插上電線，通過模擬各種電信號輸入，使得大腦以為自己活在真實世界中。

這個想法源自哲學家笛卡爾的《第一哲學沉思集》［7］，在書中他論證我們應該懷疑一切，需要逐一檢驗所有人類的知識，數學，幾何，以及感知到的世界。然而他發現除了「我思故我在」之外，所有的知識都可能不靠譜，因為我們的大腦很可能被一個具有「超能力」的 Evil Demon 所欺騙。

2003 年牛津大學的哲學教授 Nick Bostrom 鄭重其事地寫了一篇論文『我們生活在計算機模擬世界中嗎？』［8］。認為以下三個事實中，至少有一個成立：

1. 人類文明徹底滅絕。

2. 人類文明已經到達可以完全模擬現實世界的科技水平，但是處于某種原因，沒有一個人愿意去創造出一個新的模擬世界，充當上帝的角色。

3. 我們現在的人類文明就生活在一個模擬世界中。

硅谷企業家 Elon Musk 在一次公開采訪中，談到「我們生活在基礎現實世界」的概率只有「十億分之一」。也就是說，他認為我們生活在一個電腦游戲（模擬世界）中，在模擬世界之外，有一個程序員，他開發并操縱了這個世界，我們每個人都是一個游戲角色（ NPC）。

在玩膩越獄 iPhone 和自動駕駛之后，神奇小子 Geohot 在今年三月份的「西南偏南」大會上做了一個題為「Jailbreaking the Simulation」的演講［9］。他認為，我們被生活在一個模擬世界中，所謂的上帝就是外部世界里活蹦亂跳的碼農們，他們編程創造了我們的「現實世界」，當然，他們可能啟動了不止一個世界副本。然而，他們可能也生活在一個外層「模擬世界」中。

如果我們確實生活在模擬世界中，或許我們可以在地球的某個地方找到一個后門——「Simulation Trapdoor」，從而獲得「模擬器」的超能力，抽取出不可思議的「秘密知識」。

如果我們的世界的確是被程序模擬出來的，這個程序也許會有 Bug，如果有 Bug 存在，說不定我們可以利用這個 Bug 進行越獄，跳出「理想世界」，到達外面一層的世界中，與可愛的碼農上帝聊一聊。

這是在開玩笑嗎？下面摘自自知乎的一個段子［10］：

如果世界是虛擬的，有哪些實例可以證明？

1.為什么宏觀上豐富多彩，但是微觀的基本粒子卻都是一模一樣的？這正和圖片富多彩，但是像素是一模一樣的一回事

2.為什么光速有上限？因為機器的運行速度有限

3.為什么會有普朗克常量？因為機器的數據精度有限

4.為什么微觀粒子都是幾率云？這是為了避免系統陷入循環而增加的隨機擾動

5.為什么有泡利不相容原理？看來系統采用的數據組織是多維數組

6.為什么量子計算機運行速度那么快，一瞬間可以嘗試所有可能？因為這個本質上是調用了宿主機的接口

7.為什么會有量子糾纏？這實際上是引用同一個對象的兩個指針

8.為什么會有觀察者效應？這顯然是lazy updating

9.為什么時間有開端？系統有啟動時間

未完待續

設計一個密碼學協議就好像在走鋼絲，如果你想同時做到「零知識」和「可靠性」就意味著既要讓協議內容充分隨機，又要保證「知識」能夠參與協議的交互。如果協議沒有正確設計，亦或沒有正確工程實現，都將導致系統安全性坍塌。比如可能破壞了零知性，導致「知識」在不經意間泄露；或者也許破壞了可靠性，導致任何人都能偽造證明。而且這種安全性，遠比傳統的代碼底層機制漏洞來得更加嚴重，并且更難被發現。嚴格數學論證，這似乎是必不可少的。

我們的世界真的是某個「三體文明」模擬出來的嗎？不能排除這個可能性，或許，我們需要認真地重新審視自己的各種執念。不過那又怎么樣呢？至少自己的「思想」是真實的。