從去年底開始，筆者就一直很關心MimbleWimble這個新的隱私協議的發展，不只是因為Grin主網上線的緣故，或者Litecoin即將采用MimbleWimble協議的關系，而是因為他是很多隱私協議的結晶體，他巧妙地結合了許多隱私協議，而且讓隱私交易變的可以實行，甚至具有擴容的效果，因此，一直很想再寫一篇文章，把MimbleWimble的機制運作講的更仔細，同時也力求好懂。

一、MimbleWimble怎么來

MimbleWimble的發展過程有點類似于比特幣，是個千呼萬喚始出來的成果，也就是某個議題，或者某種需求討論了好久，終于有個人或者某篇論文，把一路上零零總總的研究成果，結合成一套可以運行的協議：在比特幣問世以前，很多人在討論去中心化的電子現金，例如Wei Dai;還有Adam Beck研究出「雜湊現金」Hash Cash，還有對于時間戳記（timestamp）、公私鑰等等的研究成果，加上Satoshi在共識演算法上的突破--Nakamoto Consensus，而有了比特幣；在MimbleWimble協議產生以前，其實很多在比特幣核心開發組織中的成員，開始認為比特幣的確實現了「點對點的現金交易」，但卻不夠能維護「點對點交易的隱私」，有許多研究者已經能夠從交易圖和網路爬蟲等方式，來圖像化分析某個或多個帳號的歷史交易，并接近精準的推測交易的人或者群體可能是誰。因此在比特幣交易中暴露交易雙方帳號、交易金額以及交易可追蹤等特性會威脅了交易匿名性（anonymity），而本身交易可追蹤的特性又讓貨幣本身不具有可替代性（fungibility），也是被人所詬病的特點。

于是，在比特幣核心社群Bitcoin Core中，陸續有很多人提出了各種協議，或者新的方法，想要促進比特幣能夠更具有隱私性，但都比較像是個別專案的性質，而不是一套馬上能夠讓某種貨幣直接使用的區塊鏈系統。直到有一天，在比特幣的IRC（Internet Relay Chat） channel中，有位化名為Tom Elvis Jedusor（法文版的佛地魔）透過Tor網絡放了一份txt檔，也就是后來大家俗稱的白皮書，他在里面命名了一個叫做MimbleWimble的協議（哈利波特里面的鎖舌咒語，念了你會說不出話~~），并且推測了，透過Confidential Transactions（機密交易，簡稱CT）、CoinJoin 、One-way aggregate signatures（單向聚合簽名，OWAS）等三種方式，可以完成「隱私交易」，并且透過cut-through的方式處理資料大量增加「產生的狀態增長問題」。他在留了這份名為MimbleWimble的白皮書后就人間蒸發了，然而他的白皮書仍然留下了很多問題，而且沒有完善的數學證明他的想法的可行性，是最后由BlockStream的Andrew Poelstra將這篇文章完善，提出了一篇較為完整版的論文。（對了，后面還會一直看到BlockStream，沒有這間公司的人，我認為也不會有MW協議）。

所以整體來說，MimbleWimble是在比特幣社群中，有長期關心隱私問題的專家和愛好者們，不斷的提出各種改進方法，最后有人統整這些方法，并且被人驗證后所產生的產物，和比特幣構成的過程有點相似，但是他是一個協議，實際的實作還必須等到Grin還有BEAM這兩種隱私加密貨幣的出現。

從比特幣的交易中，可以去分析個別的群體分別可能為何

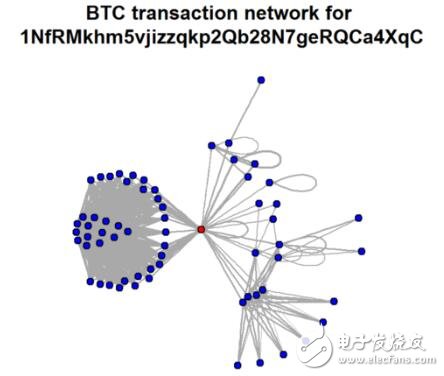
某個比特幣帳號在R語言下呈現的交易圖

二、解構MimbleWimble三大零件

Mimblewimble是個由很多個零件拼裝起來的變形金剛，在這個章節我會來介紹，MW的各種零件是如何運作來完成這套協議，根據協議，我認為MW的隱私貨幣交易有三個交易的特性。

1.沒有交易金額

2.沒有交易雙方地址

3.在一個區塊中，多筆交易是被合并的，沒辦法看到每個單筆交易的細節

要完成這樣的特性：必須分別由三個大零件：

1.Confidential Transactions（機密交易，簡稱CT）

2.CoinJoin（混幣交易）

3.One-way Aggregate Signatures（單向聚合簽名，OWAS）

透過這三大重要的主要協議，來完成隱私交易，最后透過Cut-through，來回應已確認的鏈狀態大量累積的問題，這也是MimbleWimble比Zcash和Monero等仍需要儲存許多狀態資料的隱私幣還出色的地方。

既然他是一個專門為隱私幣所創造的區塊鏈協議，那么還是先來介紹一個區塊中的內容物：

1.經ECDSA加密過的交易輸入和范圍證明的merkle tree

2.經ECDSA加密過的交易輸出和范圍證明的merkle tree

3.交易內核：一個剩余值excess value（s）和總和的kernel offsets、挖礦費用。

4.區塊頭、區塊高度

其實應該在這里就能夠看出來MW和其他區塊鏈的區塊有結構上的差別了，在此也開始解構MimbleWimble的所有零件：

1、Confidential Transactions機密交易

首先先介紹Confidential Transactions（以下簡稱CT），CT最早是blockstream的Adam Back提議添加「加法同態」的性質在比特幣交易中而產生，后來這個方法被Gregory Maxwell以Confidential Transactions的名義發出來，最后被匿名的佛地魔加到了MW協議中，他的最基礎的概念就是要將任何協議中的交易輸出及交易輸出都以橢圓曲線的方式進行加密。

所以在MimbleWimble之中，每個交易輸入和交易輸出都會以Pedersen Commitment的形式寫成：

C=r*G + v*H

Maxwell的文章中是這樣寫：commitment = SHA256（ blinding_factor || data ）

如上所寫，我們可以知道C（ Pedersen Commitment，Pedersen 可能是從TP Pedersen的論文而來）是一個讓交易金額v通過ECDSA（ 橢圓曲線數字簽名算法， Elliptic Curve Digital Signature Algorithm，縮寫ECDSA）而產生的值，這個值眾人皆知，然而透過橢圓曲線后所看到的輸入值將不再是單純的金額，我把上面算式內容分成以下三點解說：

1. r是所謂的致盲因子（blinding_factor），作為私鑰使用，是不能被其他任何人知道的，這個私鑰也代表你對這個交易值的所有權。

2. G和H則是在橢圓曲線上的兩個點，而r*G則是r在G上的公鑰，我們沒辦法透過r*G而知道ｒ值，這是所謂的離散對數問題，我們不會因為知道公鑰，就因此而知道私鑰，切記不要把這里說的乘法和5*6=30這種單純的乘法搞混。

3. v則是交易的數額，只有交易的另一方也會知道，但是礦工與其他人則不會知道。在這里橢圓曲線確保了一件事，交易金額v和致盲因子r不會被透過逆推的方式而知道。

現在你知道一筆交易的長相如何了，我們趕緊來看怎么樣可以讓這筆交易怎么被驗證。

1-1、 隱藏交易數額的魔法：加法同態（Additively Homomorphic）

在MimbleWimble中，每筆交易仍然遵守UTXO（ Unspent Transaction Output）的概念，如果對比特幣有點了解，應該還有印象當我們說某用戶的錢包“收到”比特幣時，意思是說這個錢包發現一個可以使用該錢包控制的密鑰來花費的UTXO，你可以將他簡化成輸入=輸出。

假設今天在比特幣交易中，你的帳戶有10BTC，你用了7BTC給賣家，3BTC是找零（為了簡化先不管手續費）。

輸入1（10）=輸出1（7）+輸出2（3）

可是今天我們在MW的交易中，數額是不能被外人知道的，這時候交易仍要遵守V1+V2=V3的形式，這時候同態加密（ Homomorphic Encryption ）就派上用場了，在CT中遵守的只是同態加密中的加法同態（ additively homomorphic ），加法同態的意思，就是先加密再相加=先相加再加密，因此，我們能夠看到算式演變如下：

V1+V2=V3

=》 V1*H+V2*H=（V1+V2）*H=V3*H

這時候加法同態的性質巧妙的驗證了一件事情，那就是我們不需要知道原本v1和v2，以及v3的值是多少，只需要知道V1*H+V2*H=V3*H就可以驗證v1+v2=v3了，也因此他能夠成功地去隱藏交易數額。

但是這里會存在另外一個問題，就是我們如何在輸入=輸出的情況下，不讓交易的另一方，以及后來的驗證者不知道我的私鑰，同時又可以讓他們驗證我知道私鑰呢？

可能看完你還不一定知道問題在哪里，讓我們先來看看這個問題：

今天Alice假設有24個幣，致盲因子為81，則他的Pedersen Commitment會是

81*G+24*H

那要是Alice傳給Bob數量為7的幣，那么算式會變成（ps.在此我們先忽略礦工手續費）

A-B=（81*G + 24*H）-（81*G + 7*H）=0*G-17*H

這樣就會變成說，Bob將會知道致盲因子是81，如此一來你的私鑰就被曝光了。所以在真實的MW交易中，不能讓這種事情發生，否則連你找零的花費都有可能被取走，因此當Alice要和Bob交易時，必須再另外為所找零的錢所設立一個致盲因子，例如我們將另個致盲因子設為8，記住這個8還是不能讓他知道的，同時，當你傳給Bob時，Bob也會指定一個私鑰數字（這里假設Bob的致盲因子是23），雖然這時候Bob不會知道你的致盲因子是多少，但我們能夠利用等式兩邊數值相減為零的特性，來去驗證你給的致盲因子之差的正確性。所以這個時候的算式變成這個樣子：

Alice（24）-Alice（17）-AlicetoBob（7）

81*G+24*H-（8*G+17*H）-（23*G+7*H）=50*G+0*H

這時候此筆交易中，驗證的礦工會收到50*G的余項，這時候的excess value值就是50，50*G（余項）和50（致盲因子差）則剛好可以作為公鑰與私鑰。（記得這部分的交易內容中，沒有算到礦工手續費）。

1-2、避免多余金錢被制造的魔法：范圍證明（Range Proof）

今天我們已經可以確定交易數額可以透過加法同態的方式去隱藏，并且讓驗證的礦工能夠驗證交易等式兩邊是相等的，但這時卻還有一個影響交易有效性的問題，就是即使等式兩端相等，還是有可能憑空創造出來的金錢，可能一時之間比較難想像，那你能夠先看下面這組輸入與輸出的算式：

輸入=輸出1+輸出2

5=（-10）+15

今天以上的算式，也符合輸入等于輸出的條件，但我卻能夠發現到，原本的5塊變成15塊，中間的10塊是因為是被憑空創造出來的金錢。而且這個時候負數，在橢圓曲線上對應的可能也是任何值，因此不太會被檢測出來。這時候在機密交易中用了另外一種零件，稱作范圍證明（Range Proof）。Range Proof最早由blockstream的Gregory Maxwell所提出，Range Proof會附掛在每筆交易輸入與輸出中，他透過簡單的零知識證明，可以確保在不知道數額為多少的情況下，還能證明每個單筆的輸入輸出都是一個0

然而，每筆輸入與輸出都必須附帶的零知識證明的size大小，卻是相對于交易本身要來的更大，而且礦工如果要同步于整個區塊，就必須從頭到尾都進行驗證每筆交易的Range Proof驗證，因此Range Proof本身的大小，也成為必須去改進的對象。因此，后來Stanford的學生Benedikt Bünz又在他的基礎上開發出了所占的容量更小，運算速度更快的Bulletproof，在i7–6820HQ的系統系統下實測只有688bytes的大小，較原本Maxwell開發出來的有5kb左右的Range Proof已經有非常大的容量改善，但和每筆交易差度不多33bytes相比仍然非常大。

到現在我們可以有一個概念，以了解不用知道金額的交易如何被有效驗證：

1.礦工透過Pedersen Commitment的加法同態性，確保在不知道交易金額的情況下，還能確定等式左右兩邊輸入等于輸出

2.透過Range Proof來確定某個不知道數額的交易輸入或輸出，確實大于零，以避免被憑空創造出新錢。

2、CoinJoin 混合交易

在過去有許多人認為在比特幣的交易圖上，能夠看到「哪筆輸數對應到哪筆輸出」是一件非常容易暴露隱私的地方，因此Gregory Maxwell（是的，又是他）題出了一個叫做CoinJoin的概念，他要做的事情非常簡單，就是將兩筆交易混合。

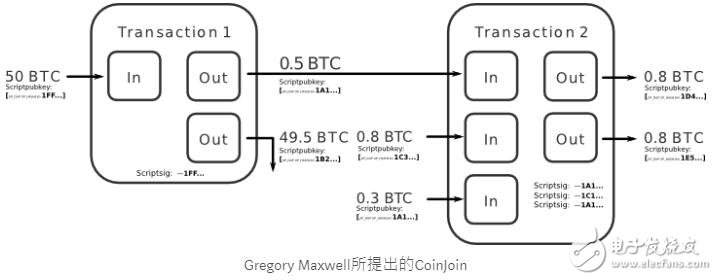
在MW協議以錢，有許多錢包或者額外的服務，就有配置CoinJoin的服務于其間，例如WasabiWallet和Tumblebit、JoinMarket，然而單靠Coinjoin卻依舊是不安全的，大家仍舊可以從交易數額中試圖去還原，同時因為是個別的服務，參與的人數太少，在資金匹配上也需要花一定的時間。這時候佛地魔在MW協議中將CoinJoin的技術，結合機密交易（CT），就能夠避免交易能夠從「數字」方面去被推敲出來，同時在交易路徑上也可以透過CoinJoin的技術被混淆。

而且和過去個別使用CoinJoin的服務不同的地方，是這次Mimblewimble，徹底把CoinJoin寫在了協議層，如此一來不需要靠第三方的錢包或者服務幫忙就能完成這一件事情，而且有機會讓混合交易變的更有效率。

但現在就要開心的慶祝隱私交易的魔法能夠實現，就還太早了，因為即使混合交易數額，我們還是能夠知道交易雙方的公鑰，并且能透過這些公鑰址去嘗試重構每一筆交易，因此在這樣的情境下，我們必須要有新的公私鑰系統，來確保隱私安全。

3、OWAS （ One-way Aggregate Signatures，單向聚合簽名）

Jedusor在他的初略版白皮書中，提出了可以用Yuan Horas Mouton的單向聚合簽名（ One-way Aggregate Signatures，簡稱OWAS）的方式去完成，比較有趣的一點是在Andrew Poelstra在他詳細版的白皮書中，卻沒有用到OWAS這個詞，而是在Sinking Signature還有compact chain中去驗證這個技術，甚至連后來開發Grin的Ignotus Peverell的Github的MW簡介中，也沒出現OWAS這個詞，而是直接說Transaction Aggregation（交易聚合），不知道這個專有名詞，為什么在這個三個重要的MW文件中，出現的方式會略有不同，但在此還是以OWAS去代稱（我知道在之前已經有如Boneh等學者在研究聚合簽名 ）。

所謂的聚合簽名，就是指當你看到很多交易的輸入以及輸出時，我們將不能再把這些輸入及輸出的公鑰重新拆解，并且拼湊出一個完整的交易順序，因此我們將所有簽名聚合在一起，并且不能使他逆向被還原。

OWAS由兩個部分組成，一是Kernel Excess（內核剩余），一是Kernel Offsets（交易核偏移因子），還記得我們所說的致盲因子之差嗎？對的，就是Alice既要傳送錢給Bob，又不希望Bob知道他的私鑰（致盲因子），于是他給他了（致盲因子差）*G，這時候我們為了避免人家從交易中的公鑰推測出交易途徑，我們用了單向聚合簽名的方式來降低大家知道這個值的可能性，因此我們產生了以下算式

輸出的Confidential Transactions總額-輸出的Confidential Transactions總額= Kernal_excess + kernel_offset

透過這種方式，我們就可以將最后作為的公鑰的余項（例如剛才上面在講機密交易時的50*G）拆分成兩部分，例如X*G拆成（x1+x2）*G ，這時候大家能構讓外界看到的值x1*G就是所謂的Kernel Excess，你可以把它看作是公鑰；而另外一部分就是x2*G，稱作Kernel Offsets，他會和這個區塊中所有交易的Kernel Offsets一起被相加，而當他們這么多個Kernel Offsets被相加后，你也就看不出來，哪個Kernel Offset是哪一筆交易中的了，所以這個方法才會被叫做單向聚合簽名，因為他沒辦法在做逆向工程了。因此，當一筆MW上的交易在給礦工驗證時，我們可以想像Kernel Excess就是公鑰，而Kernel Offsets是私鑰。

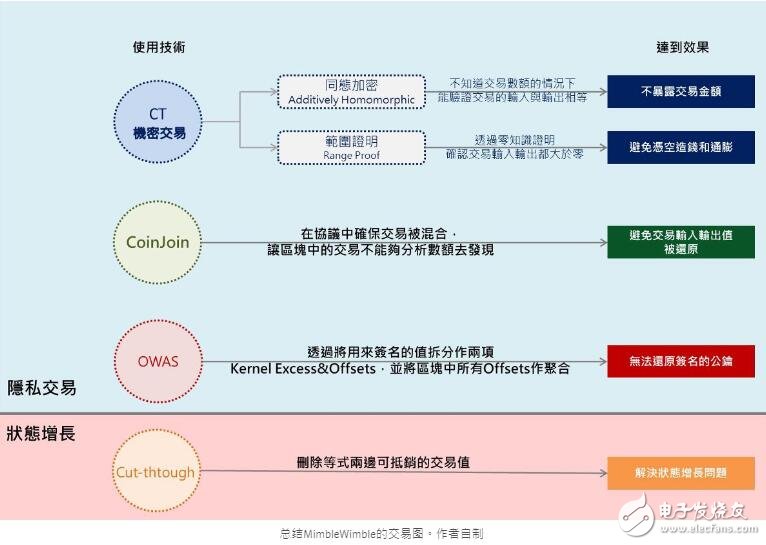
到此，隱私交易的部分就徹底完成了，我們在此簡短重復一次

1-1、機密交易-加法同態：確保在不知道交易金額的情況下驗證等式兩邊成立

1-2、機密交易-范圍證明：確保在零知識證明下，每個輸入輸出值大于零，避免憑空創造多余金錢。

2、混幣交易：讓我們無法從交易數額中去回推交易路徑

3、單向聚合簽名：讓交易的公鑰不會被暴露出交易路徑

三、Cut-through核銷：減少礦工儲存狀態

cut-through是MimbleWimble中一個針對礦工的精巧設計，他能夠確保的是礦工不需要長期存儲這么多的交易狀態，而cut-through的概念就是在一筆交易已經被確定其所有權的情況下（也就是被驗證）后，只要能夠維持輸入等于輸出（input=output），那么過程中多余的內容都可以被刪除。

例如原本的幾個交易可能長這個樣子

Input1+Output1=Ouput1+Change1+Output2+Change2

=》Cut through之后（Output1等式兩邊都有因此可以被刪去）

Input1=Change1+Output2+Change2

然而在這里必須特別說明，我認為Cut-through的概念并非能夠在目前實作的兩個項目中（Grin&BEAM），達到很好的隱私，例如在Grin中，其實Cut-through的功能是能夠被關掉的，只要將~/.grin/main/grin-server.tomlar的archive_mode從

archive_mode = false

變成

archive_mode = true

in ~/.grin/main/grin-server.toml

如此一來礦工的節點就不會執行核銷的動作。因此我認為目前部分外界人士，可能認為Cut-through能夠透過刪除資料來解決隱私，就目前的實作來看可能會是一個誤解。

四、MinbleWimble的后續效應與限制

MimbleWimble不但是一個許多隱私協議所組成的隱私幣區塊鏈協議，更是許多過去比特幣社群所遇到問題時，一些原本在比特幣上無法實現的好方法被應用的好場景，然而MimbleWimble也像是練就了某種神功后，具有某些后遺癥的武者，因此在最后，我試圖去探討，MimbleWimble會產生什么后續的影響，以及發展可能有什么樣的限制。

1.挑戰其他隱私幣的地位和公鏈設計原則

筆者認為，MimbleWimble協議所影響的，首先是挑戰既有隱私幣的地位，例如Monero和Zcash，MW協議中不但不需要為了驗證交易的合法性，而保留以驗證的交易作廢清單，同時Cut-through的功用，也讓礦工能夠減少儲存已驗證的狀態這種較為不合理的手法。另外，我認為MW協議也是少數，用減少資料儲存來達到可擴展性的公鏈設計手法，同時他也減少了許多區塊鏈中應該要被礦工所記載的內容，在MW中，一筆交易里面礦工要知道什么：最主要的就是交易有效性與通貨膨脹，可能會影響未來不具高度智能合約需求的貨幣項目，往這樣的方向去發展。

2.限制

雖然MW在隱私協議上采取了非常巧妙的手法，去實現了匿名交易。但其本身依舊有某一些限制，在此我將他分為三點：一是Range Proof所占的容量影響交易狀態儲存的容量；二是交易實作上的使用體驗；三則是智能合約等等貨幣交易以外的區塊鏈功能實現能力。

2-1、Range Proof所占的容量影響交易狀態儲存的容量

上文曾經說過，透過Cut-through，我們能夠減少礦工的儲存內容物，避免狀態大量累積的問題，然而，在MW區塊鏈中，無法被刪減的，是每筆輸入與輸出中的范圍證明（range proof），Range Proof是一個簡單的零知識證明（688bytes），容量相較于交易訊息本身（單個交易約33bytes），相較而言其實是非常大的差距，這也是會影響未來礦工儲存資料，以及未來可擴展性的關鍵。

2-2、共同構建交易的實作體驗

在MW協議下的交易，我們必須要交易雙方共同去將一筆交易完成，例如Alice寄錢給Bob，Bob必須證明他知道交易金額，并且在回傳訊息給Alice，最后交易經過Alice驗證運算后才完成，這樣的過程不需要同步在線上完成，但需要交易雙方共同構建，和比特幣、以太坊等等密碼貨幣那種只需一方傳送金額簽章到區塊鏈上的概念較為不同，因此目前例如在Grin上，有兩種方式可以進行交易：

· 寄送檔案： Bob需要收到交易檔案（ transaction file），并且生成一個回應的檔案（response file），并且寄回給Alice。

· 網頁（HTTP）： Bob的Grin錢包必須要監聽一個端口。無論Alice的錢包什么時候寄給他，Bob的錢包都會自動執行既有的步驟。但這卻有一個比較苛刻的條件，就是錢包需要在一個固定的IP地址下，并且你的錢包客戶端要持續運作才能完成。

這些過程其實都是非常不人性，很難在未來普及使用。目前Grin有開發一個新錢包grinbox，目標是能夠像比特幣一樣的交易，但很持續在開發中，如果未來有任何消息，我會持續更新。

2-3、貨幣交易之外如智能合約等功能的擴展現制

MimbleWimble和比特幣較為不同的是其較難支持區塊鏈中的交易腳本，這也導致了如比特幣可以實現的簡單智能合約、或者閃電網絡等等，然而，我認為這或許是大家已經不太震驚的MW缺點所在了，而且目前就筆者所見，已經有一些有趣的專案被展開，例如精確版MW白皮書的撰寫人：Blockstream的Andrew Poelstra，目前正在研究透過無腳本腳本 （ scriptless-scripts）的方式來創造MimbleWimble上簡單的應用，同時也有人實現了Grin上的原子交換。或許未來可能有更輕巧的智能合約實現方式出現。