最近針對動力電池多并狀態(tài)下,電芯通過電流不一致性的問題做了些研究,有些蠻有意思的結論。
1)電芯成組基本方案
現(xiàn)行的車用動力電池,在電芯組成模組時的并聯(lián)方案,有幾種情況:
對于較大容量的軟包或者方殼電芯,在模組一級有2P、3P、4P幾種狀態(tài);
對圓柱方案并聯(lián)數(shù)則比較多,像特斯拉是40-50P這種量級。
為保證并聯(lián)在一起時各電芯的表現(xiàn)一致,電芯制造企業(yè)需要盡可能保證出產(chǎn)電芯的一致性。然而不可避免的,批量生產(chǎn)中必然或多或少會存在隨機的不一致性,這種不一致性應該呈現(xiàn)圍繞著中值的正態(tài)分布(內阻、容量等),先留意,后面進一步分析中會用到這個前提。
先以一個簡單的模型對這種不一致性形成的影響做個簡單的定量理論分析。為方便地見,假設其中一個電芯的內阻出現(xiàn)偏差,則(無論直流還是交流,U=IR成立)相應的支路電流會相應反比例出現(xiàn)偏差(注:實際會出現(xiàn)多個電芯參差不齊的情況,但對于最弱的電芯計算結論相差不大)。
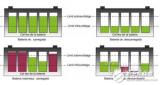
如下圖,電芯標準內阻為r,其中一個電芯發(fā)生偏差導致各支路電芯電流出現(xiàn)不一致。
I0是理論均勻情況下每個電芯的電流,母線上總電流是n*I0;比如假設4P電池允許5C放電,母線電流理論上會是4*5=20C。發(fā)生偏差時,其它n-1個均勻電芯電流為Ir,一個差異電芯電流為Iv,總電流仍為n*I0=(n-1)*Ir+Iv。
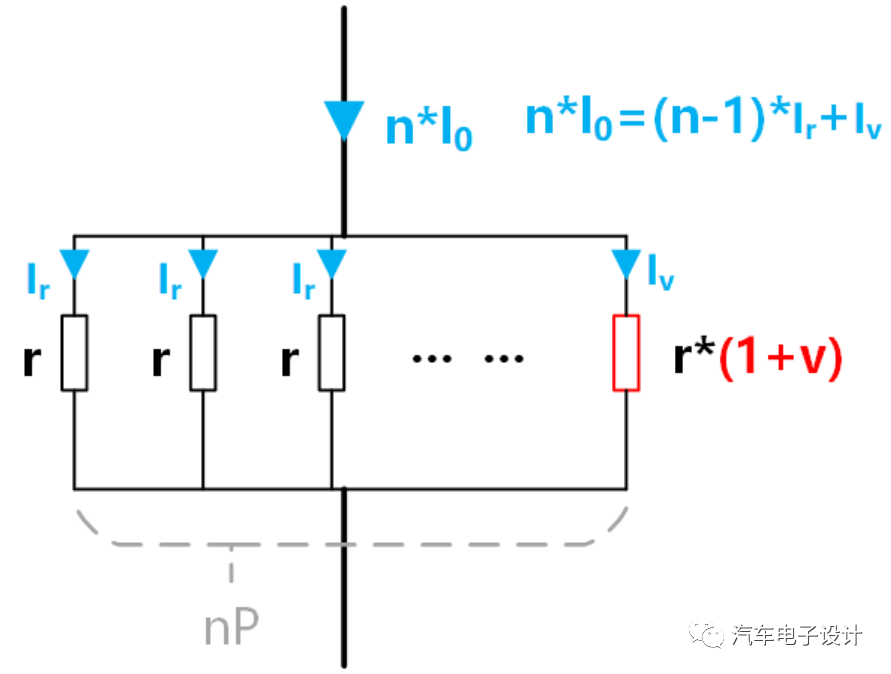
做點不復雜的計算,可以得出下面兩個式子:
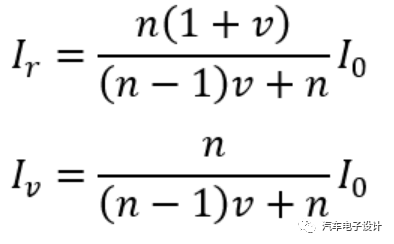
然后根據(jù)式中的v和n兩個變量,可以畫出如下的圖(坐標軸電芯內阻偏差v取±30%,并聯(lián)數(shù)n取2到50)。
為后面敘述簡明起見,在此做個定義。用并聯(lián)電芯中,最大的支路電流與理想均勻情況下電流的比值,來衡量一組并聯(lián)電芯電流的不均衡性,即:
Cell Parallel Current Imbalance: CPCI = Iv/I0。
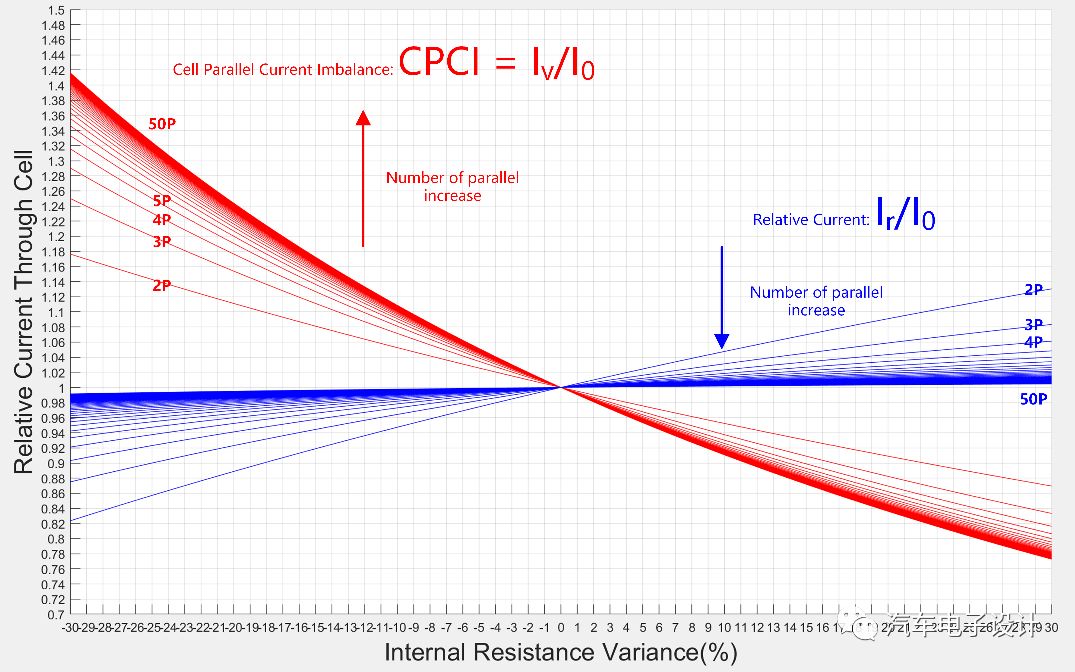
從圖中有幾點需注意的:
同樣的電芯內阻偏差,并聯(lián)數(shù)越高,電流不均衡性越強;
然而隨著并聯(lián)數(shù)增加,不均衡并非線性增加,對增加的并聯(lián)數(shù)越來越不敏感(例如Tesla Model3已經(jīng)多達46P,在這個數(shù)量區(qū)間,并聯(lián)數(shù)多點少點對電流不平衡的增量影響幾乎可以忽略);
內阻最小的電芯承受了最高的支路電流,與內阻偏差關系總體比較線性。
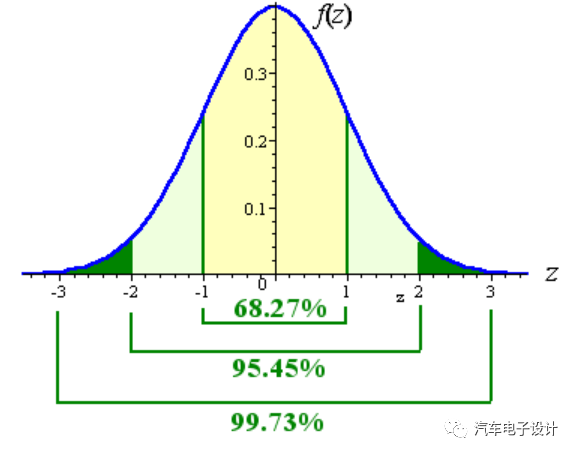
以上是個非常簡單的理論模型分析。實際情況,電芯的內阻散差是按正態(tài)分布規(guī)律分散的,并且在電芯下線時有篩選標準。簡單來說,按照正態(tài)分布,
如果內阻下線檢測標準在±σ內,環(huán)節(jié)良品率大約有68.27%
如果內阻下線檢測標準在±2σ內,環(huán)節(jié)良品率大約有95.45%
如果內阻下線檢測標準在±3σ內,良品率大約有99.73%
以上是正態(tài)分布的自然規(guī)律,對于電芯企業(yè)來說,提升良品率重要的是控制標準差σ的絕對值,使它盡可能小。如果標準差很大又追求高一致性,那就只能提升良品率標準,帶來的是廢料的增多和成本的增加。
從下線的合格電芯中隨機配組,全部配成并聯(lián)狀態(tài),肯定也會存在各支路電芯的不均衡。那么接下來提出一個問題:所有并聯(lián)電芯組中,針對不同的不均衡水平,分別有多大占比?
這其實是個數(shù)學問題,每個電芯都符合正態(tài)規(guī)律 X~N(μ,σ),隨機抽取并聯(lián)后,最弱支路的電流應該能算出一個新的分布。
然而眼下有限的數(shù)學技能也已經(jīng)還給老師了,無力做這么復雜的推導 。不過不要緊,還有種辦法叫數(shù)學試驗,我按以下步驟通過程序實現(xiàn):
隨機生成大量內阻符合正態(tài)分布的電芯;
按照自定的檢驗標準,去除不合格電芯;
然后再把合格電芯隨機配組成并聯(lián)組;
計算每個并聯(lián)組的電流不平衡,再做統(tǒng)計分析;
按照上面的思路,隨機出100萬個內阻正態(tài)分布的電芯,其中參考一些實際的電芯數(shù)據(jù)取5%為標準差,并取±2σ/±3σ為合格品區(qū)間,然后隨機配組后,求出其電流最大的支路的電流并統(tǒng)計分析,得出下圖結果,橫軸均為CPCI。
柱形圖是每個區(qū)間段占從并聯(lián)組數(shù)的比例,下方曲線是柱形圖的累積值。
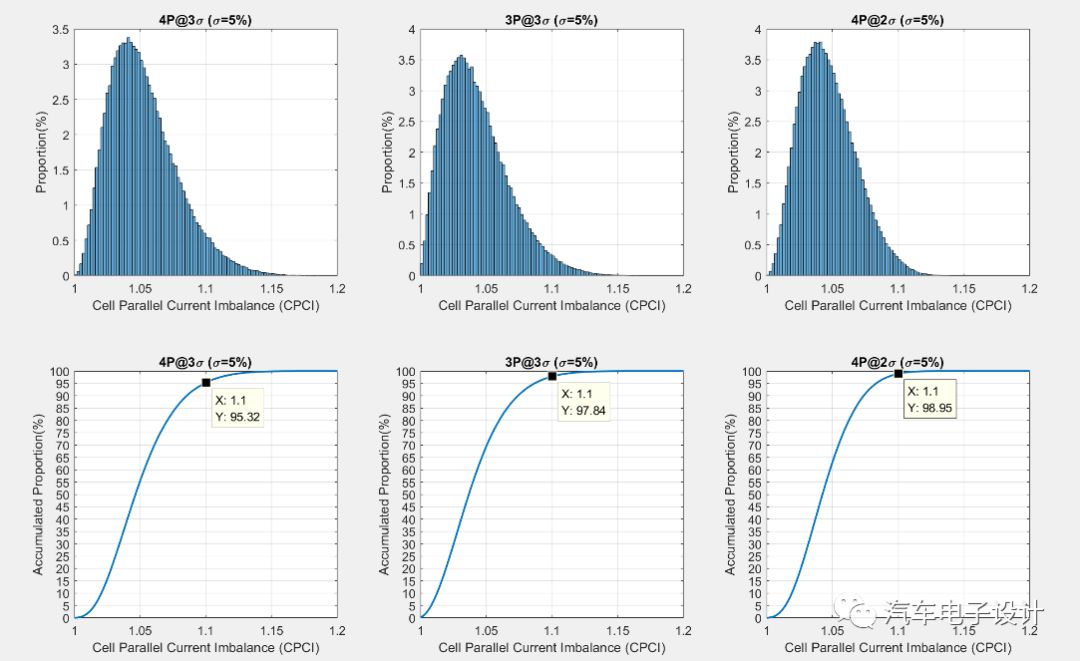
解讀一下這幾張圖:
4P并聯(lián)組概率高點大約在1.04,3P大約在1.03,相差不大;
4P的分散程度比3P明顯要寬一些;
以1.1倍電流為例,同取±3σ的合格區(qū)間,4P的并聯(lián)組約有95.3%在1.1倍以下(約4.7%超出1.1倍),3P的并聯(lián)組接近97.8%在1.1倍以下(約2.2%超出1.1倍);
以1.1倍電流為例,同是4P并聯(lián)組,如果取±3σ合格區(qū)間約有95.3%在1.1倍以下(約4.7%超出1.1倍),如果取±2σ則接近99%在1.1倍以下(約1%超出1.1倍);
但其中關鍵因素是標準差σ,上面取5%只是個典型估算,取決于各家廠商的批量一致性控制能力。為了更好的衡量標準差σ,也就是電芯廠商對一致性控制能力的影響,將σ作為變量,以4P并聯(lián)組為例,再做一組曲線。
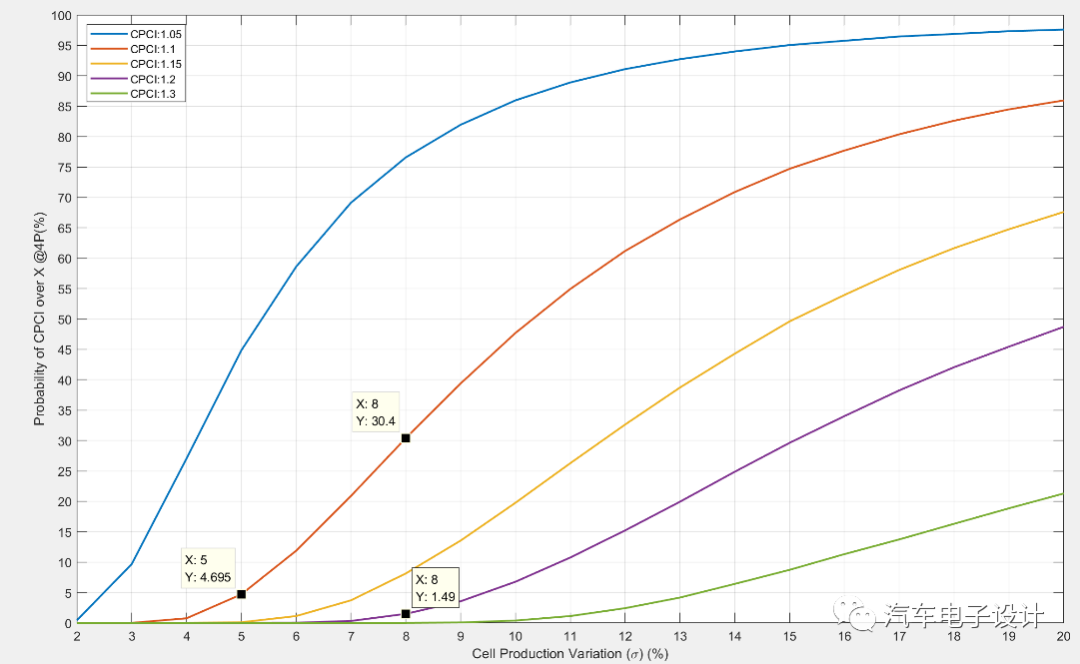
上圖表示的是隨著σ變化,4P并聯(lián)組中電芯電流的不均衡性。
以圖中標示的三個點為例解釋,兩個點標示在CPCI=1.1的曲線上。當電芯σ=5%時,則組成4P并聯(lián)組后約有4.7%的并聯(lián)組其不均衡性會超過1.1;而當σ=8%時,則會增加到約30.4%比例的并聯(lián)組CPCI超過1.1;甚至于還會有1.5%比例的并聯(lián)組會超過1.2。這意味著,假設電芯規(guī)格書規(guī)定了放電倍率能力是5C,在實際使用進行峰值功率放電時,其中約有1.5%的模組中有支路電芯承受實際是超過5*1.2 = 6C倍率!
上面的數(shù)據(jù)是基于并聯(lián)組分析的,接下來再深一步,在電動車上會把很多個并聯(lián)組串聯(lián)成PACK使用。那么表現(xiàn)在電池PACK層級,上述概率會有怎樣的進一步作用呢?市場上的電動車串聯(lián)數(shù)大約會在84-108串。我們來做個計算,以上面的1.5%(CPCI>1.2,σ=8%,3σ良品率)數(shù)據(jù)舉例:
如果一個PACK是4P84S,技術指標要求CPCI不得超過1.2。則不滿足要求的概率是:

而串數(shù)增加到108時,這個值會達到80%!真是不算不知道,一算嚇一跳。
當然,上面舉例的σ=8%有可能偏大。公允起見,繁瑣一點,分別取電芯σ=2%、5%、8%、12%幾個點,取2P、3P、4P三種模組,分別計算PACK中串聯(lián)數(shù)是84和108時,PACK中含有至少一串不均衡性超過對應CPCI值的可能性,供不同的定位參考。
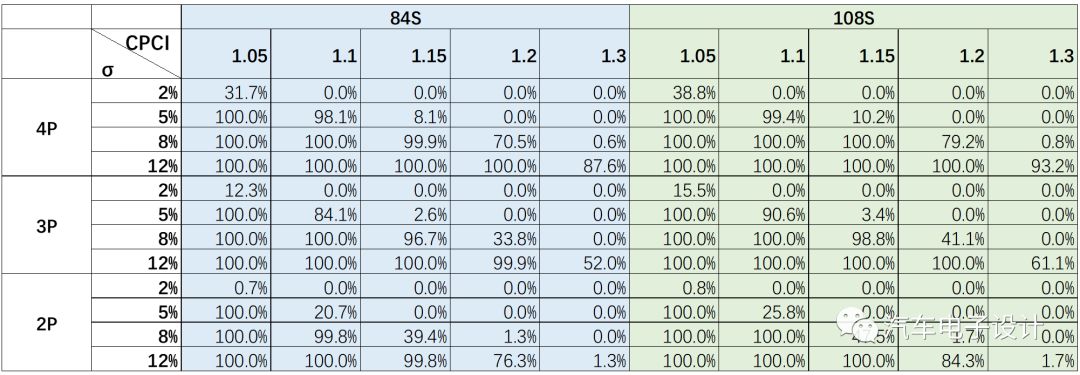
從上表可以看出,控制PACK上的不均衡性,關鍵點還是在于控制電芯的生產(chǎn)一致性。
實際行業(yè)應用中,電芯廠商在性能規(guī)格書中提供的數(shù)據(jù),一般都留有充分的性能裕量。因此多數(shù)情況下,即使電流不均衡,也落在性能裕量的容許范圍內。
但有以下幾種因素,也不得不加以考慮,
在某些性能極限的工況,例如低溫情況下充/放電能力不足,裕量幾乎沒有的情況;
隨著電芯的使用,內阻的散差會越來越大,遠超出廠的水準;
在動態(tài)工況下,內阻的散差也有可能變大;
除了電芯外,模組的焊接工藝也可能加劇各電芯支路電阻的散差。
當一個電動車項目批產(chǎn)到萬臺量級以上時,上表中每0.01%的概率,就代表一萬臺中會有一臺車,存在某電芯支路一直承受著大幅超過設計狀態(tài)的電流,這種情況無疑是危險的。
要解決這種風險,要多管齊下:
根據(jù)項目的串并配置,通過上述計算,對源頭的電芯制造、模組制造等環(huán)節(jié)提出一致性的指標要求;
通過試驗,計算不同工況以及一定循環(huán)次數(shù)后內阻的散差會不會有異常放大;
在電芯的使用上,留足性能裕量,根據(jù)上述計算思路,保證突破電芯的安全邊界的概率降低到可接受的范圍。
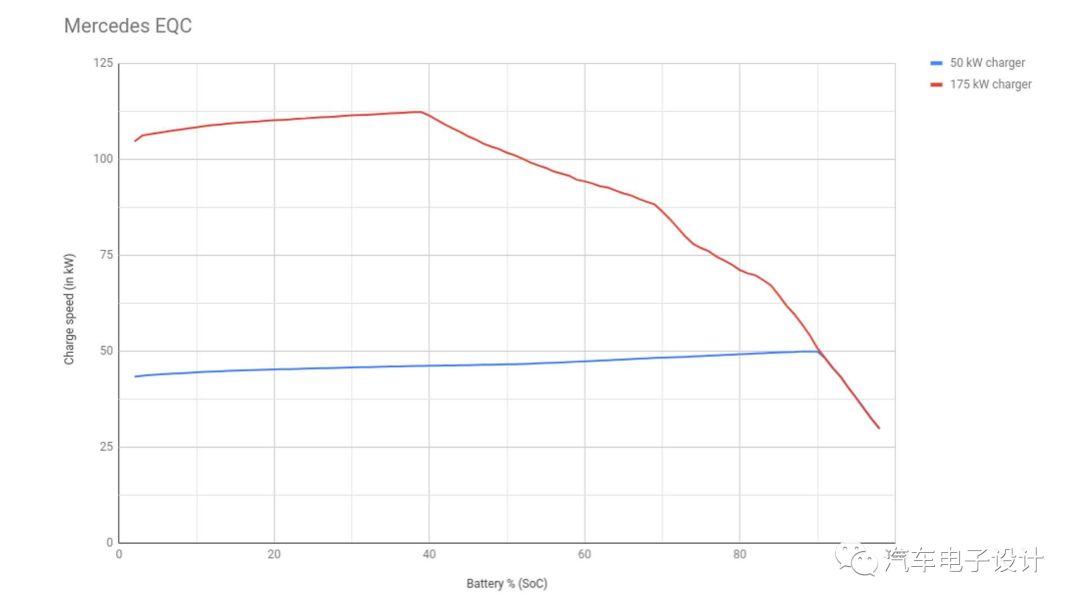
【本文是JiangxinAuto拋磚引玉的作品,這個在快充往300A這個層級做的時候,如奔馳EQC這樣的方案,這個電芯和兩個Pack分流的時候會特別明顯,一般的電芯在一致性沒辦法達到的時候,不能設置這么高的閾值】
-
動力電池
+關注
關注
113文章
4534瀏覽量
77650 -
電芯
+關注
關注
14文章
726瀏覽量
25865
原文標題:關于多并模組電芯間不一致性的討論
文章出處:【微信號:QCDZSJ,微信公眾號:汽車電子設計】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
鋰電池成組不一致及優(yōu)化方案
鋰離子電池組一致性的含義與不一致性的改進措施
感興趣區(qū)域不一致性決策算法
關系數(shù)據(jù)不一致性的修復
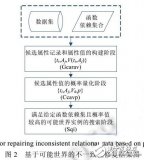




 動力電池多并狀態(tài)下電芯通過電流不一致性問題研究
動力電池多并狀態(tài)下電芯通過電流不一致性問題研究











評論