電子工程師，無論是數字還是模擬，現在必須了解如何使用傳輸線。今天需要更好理解的是IC，它產生的信號上升和下降得如此之快，以至于它們會導致互連成為傳輸線。此行為可能會改變波形和時序，甚至會損壞組件。

上升和下降時間現在短至100 psec。當呈現這樣的快速信號時，許多互連表現為傳輸線，即使它們在受到變化更慢的信號時也不這樣做。即使系統的時鐘頻率保持適中，也可能產生傳輸線效應。通過了解傳輸線的模擬特性，設計人員可以防止互連限制其系統的速度和可靠性。

本文解釋了傳輸線是什么以及它們如何工作。它包括有關正確端接如何使您能夠使用傳輸線的基礎知識。

您應該關注系統互連的速度，因為電子信號以很快的光速傳播。在典型的印刷電路板上，信號穿過12英寸（30厘米）的互連需要大約2納秒。幾年前，當門延遲為5到10納秒時，信號通過IC的傳播時間可能是幾十到幾百納秒。因此，一小部分納秒甚至2納秒不是總信號傳播時間的重要部分。

然而，在過去的十年中，邏輯門延遲已經減少到僅僅幾分之一納秒（在一些0.25毫米，3.3V ASIC中為50微秒）。上升和下降時間小于500 psec。此外，雖然現在更多的功能適用于典型的IC，但是典型的印刷電路板現在執行許多附加功能，而電路板尺寸沒有明顯改變。因此，信號在印刷電路板上從一個地方到另一個地方的時間已成為系統速度的一個重要因素。

傳輸線路不正確會導致以下問題：

振鈴延遲會導致系統速度降低：

A互連上的高速信號轉換表現為不正確終止的傳輸線，可以產生反射。反射導致臨時振鈴（電壓振蕩高于和低于最終穩態水平）。避免振鈴后果的一種方法是在允許系統處理新數據之前等待反射消退。要實現額外延遲，可以為每個操作添加一個或多個時鐘周期，或者可以降低系統的時鐘頻率。

過沖超過最大IC電壓額定值：

反射可能導致電壓升高，或者由于負過沖，降至最低額定值IC以下的最大額定值。當過電壓持續超過一小部分時間時，IC過載并可能閉鎖。閂鎖可能導致暫時或永久性損壞。 （閂鎖是寄生npn晶體管導致CMOS電路停止工作甚至毀壞自身的結果。）

串擾會增加誤碼率：

反思不正確端接的傳輸線會產生更大的電壓和電流，從而輻射出更大的電場和磁場，并將更多的串擾能量傳遞到相鄰的電線中。

下沖會增加誤碼率：

顯示振鈴從其初始最高 - 最高或最低 - 低電平回退（下沖或回鈴）的信號。如果信號退回太遠，接收IC可能會將其讀取為錯誤的值。如果信號在時鐘線上，則可能導致誤觸發。

降低的噪聲容限會增加誤碼率：

在某些配置中，不正確的端接線會導致半個或更少 - 在過渡期間存在超全振幅信號電平。一個小的噪聲脈沖可以攜帶一個信號，該信號小于閾值上的最終幅度電平，在那里它可能顯示為錯誤數據或可能導致錯誤觸發。

驅動器過載會降低信號完整性，速度和元件完整性：

有時，設計人員可以認為實際上是50W傳輸線的電線僅僅是與高阻抗負載（例如10kW）的低頻連接。低線路阻抗會使驅動器過載，因此負載電壓可能永遠不會達到正確的值。

如果互連沒有終止，為什么信號完整性會很差？

在某些條件下，互連不再是簡單的一對電線和表現為傳輸線，具有不同的特性。術語“導線”包括所有類型的導體：印刷電路板上的跡線，雙絞線，帶狀電纜和同軸電纜。

什么區別一對來自傳輸線的電線？

互連的長度和最高頻率的信號分量是決定因素。

短互連或工作在低電平的互連頻率表現為一組集總電路元件，例如一個電容器和幾個電阻器（圖1a）。典型的印刷電路板的互連電阻通常無關緊要，因此，在計算互連延遲時，只需要考慮電容。

如果互連很長或信號頻率很高，則互連表現為傳輸線，其具有明顯不同的特性（圖1b）。例如，在1 Hz時，通過長電纜驅動100 kW負載的電路將電纜視為與100 kW負載串聯的1W電阻。但是，在300 MHz時，驅動器只能看到電纜的特征阻抗，其中包括連續均勻的電阻，電感和電容。在300 MHz信號轉換期間，驅動程序沒有看到100 kW的負載。

本文試圖回答以下問題：

什么是簡短的和長互連？

什么是低頻和高頻信號？

什么是傳輸線？

傳輸線與簡單互連有何不同？

傳輸線如何損害信號的完整性？

如何正確終止修復信號完整性問題？

短互連

短互連是指長度只是信號正弦波長的一小部分。一小部分的保守經驗法則是十分之一。例如，您可以將32英寸長（81厘米）的互連視為高達24 MHz的信號頻率的集總電容。你到達那個頻率因為320英寸（8.2米）是32英寸的十分之一的波長。波長為8.2m的信號頻率為24MHz。你可以從以下公式得出這個頻率：

所以，頻率=（198 * 10 6 m/sec）/8.2m=24 MHz。如果使用網絡分析儀測量32英寸長電纜的阻抗，則電纜似乎是一個簡單的集總70-pF電容（圖2）。

波長參考：

以下是某些參考頻率的波長：

波長= =電磁波移動相位變化360°的距離。

這種關系很簡單distance = velocityXtime公式 = c 0 * T，其中c 0 =光速，T =信號周期，f =信號頻率。 = c 0 * 1/f。

這些值適用于自由空間中的電磁波。隨后的討論涵蓋了與導體相鄰的介電材料的影響。電介質的影響是前面關于短互連的討論中出現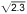因素的原因。

短長度互連看起來像一對導線和一個簡單的電容器。

通過電阻對電容充電的RC時間常數公式決定了通過短路或低頻互連的信號延遲（圖3）。印刷電路板上導體的電阻通常太小而無法考慮，但在計算時間常數時應包括驅動器的輸出電阻。例如，對于R O = 50W的驅動器，電路板走線電容C = 50 pF，以及快速5V輸入脈沖，信號在一個時間常數（t = RC）中為3.15V。另外，在t = 2.5nsec時，V = 3.15V（5V的63％）;在t = 5.0nsec，V = 4.30V（5V的86％）;在t = 7.5 nsec時，V = 4.75V（5V的95％）。

互連的傳播延遲是從施加新信號到信號達到接收器切換閾值的時間。/p>

銅導線是否決定印刷電路板互連上的最大信號速度？

這樣的討論一，專注于低頻現象，應考慮通過大塊銅導體的電流速度。該電流表示當向導體施加電勢時發生的電子（和“空穴”）電荷的流動。圖4中的公式顯示了此電荷流的速度。在極低頻率下，基于電荷的電流有時間流過導體的大部分。然而，對于高速電子系統，大約6厘米/秒的速度完全不合適。您現在應該能夠理解為什么工程教科書將此電荷流稱為“漂移電流”。

那么，高速信號如何在印刷電路板？

高速信號在印刷電路板上作為電磁波以大約一半的光速（15厘米/秒，或6英寸/秒）在導體表面和印刷電路板電介質上傳播。光也是電磁波，以30厘米/秒的速度在自由空間中傳播（C 0 = 300 * 10 6 m/sec，或186英里/毫秒）。

什么是長互連？

您可能已經猜到，雖然短互連小于信號波長的0.1，但長互連長于信號波長的0.1。基本準則是您必須將傳輸線狀態賦予任何長度是信號波長的重要部分的互連。但是，您應該認識到，對于脈沖波形，上升時間比波長用于確定互連是長還是短，更容易使用。

互連共振：

互連長度接近信號波長的四分之一，互連開始諧振，不再像集總電容那樣工作。例如，圖5中的32英寸長電纜是60 MHz信號波長的四分之一。

d = vt = v/f，andf = v/d =（3 * 10 8 m/sec/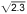）/（4X32英寸×1英寸/39英寸）= 60 MHz。因此，這種共振現象是不具有接近波長四分之一的互連長度的原因。

元件尺寸與波長的關系：

圖6顯示100-MHz，1- GHz和10GHz電流信號頻率。在100 MHz時，2 cm長的電阻中的電流在整個電阻上是相同的。在1 GHz時，電阻中的電流在每端略有不同。您甚至無法在10 GHz處定義集總電阻器中的電流，但是：在一端，電流為正;在另一端，它是消極的。傳統元件的分布特性是在如此高的頻率下使用小型薄膜電阻器的一個原因。

什么是高頻互連？

高頻互連是指信號的上升時間（t R ）小于傳播時間的兩倍（t） PD ）或飛行時間，信號的電磁波到達互連的末端。

盡管波長標準說明了一個基本原理，但這種上升時間規則更容易使用，并且應該形成決定互連是否表現為傳輸線的基礎。原因很簡單：所有數字信號都包含高于基波的頻率分量。為了產生尖角，方波至少包含三次和五次諧波。雖然您可以使用這些諧波的頻率，但大多數數字系統設計人員都會考慮上升和下降時間，這些更容易使用示波器進行測量。如果無法測量上升和下降時間，則可以估算它們。通常情況下，每次都是10％到20％的時間。

設計人員不應該陷入這樣的陷阱：他們認為IC的上升時間是那些數據表上的時間。大多數數據表甚至沒有指定上升和下降時間，但數據表通常只提供最大（最慢）值。您收到的部件可能至少稍快一些，并且可能快幾倍。因此，您應該使用基于制造商保證或自己測試的上升時間數字。

對于32英寸長電纜的早期示例，您必須將電纜視為用于頻率大于24 MHz的信號的傳輸線。以下公式說明了這一點：

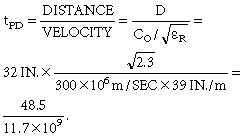
其中t PD 等于4.15 nsec，這是電磁波進行單程旅行所需的時間。 2t PD 數字等于8.3 nsec，這是雙程旅行所需的時間。因此，如果上升時間小于8.3納秒，則該電纜是傳輸線。如果假設上升時間為信號周期的20％（0.2T = 8.3nsec），則T = 41.5nsec，頻率= 24MHz。因此，對于頻率高于24 MHz的信號，此電纜是傳輸線，其中是相對介電常數（RG-58電纜為2.3），C O 是光速（300X10 6 m/sec）。

為了節省計算時間，您可以使用一個圖表來顯示不需要終端的線對和傳輸線之間的邊界（圖7）。數據基于印刷電路板上的互連長度和信號的上升時間。

互連波形

圖8顯示了沿簡單導線和沿傳輸線的信號傳播。該圖顯示了信號幅度與特定時間沿線的距離。對于短互連或低頻信號，施加的信號電壓瞬間出現在互連的每個點上（圖8a）。 （如果通常在印刷電路板和短電纜上，電纜的RC時間常數小于信號的周期，則傳播是瞬時的。）

實際上，信號的電磁波沿著電纜的有限速度傳播。從源到負載的互連（如果有反射則返回）。然而，這一運動并不明顯。在每次振幅變化之后，波經常從光源傳播到負載并返回，瞬態太小而無法觀察。

然而，對于長互連或高頻信號，電磁波傳播時間與上升時間相當（圖8b）。因此，瞬態入射和反射波振幅在大小上與施加的信號相當。因此，通過圖8中的t 1 ，所施加的信號電壓僅從源端行進了一小段距離。只有經過一段時間后，t 2 ，電壓才會出現在靠近負載的位置。

信號沿著傳輸線沿著接近光速的速度作為電磁波傳播。在自由空間（例如天線）中，導體旁邊沒有電介質（絕緣）材料，信號的電磁波以光速傳播。在印刷電路板上，由于互連導體附近的介電材料，電磁波的速度較低。

電路板互連上的電磁波速度等于光速除以光速的平方根。與導體相鄰的材料的相對介電常數。例如，在由FR-4材料制成的板上，相對介電常數（ R ）= 4，并且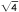 = 2。因此，電路板上的信號速度是光速的一半（1.5 * 10 8 m/sec或6 in./nsec）。

波傳播

波浪的概念是物理學中最重要的統一概念之一。物理環境有許多類型的波：光波，聲波，水波，熱浪，無線電和電視波，地震波，甚至交通波。移動波攜帶能量。大多數波浪穿過介質，如地球，空氣，水和鋼，而不是實際攜帶物質，盡管它們需要物質傳播。

水波例證了需要中間材料的波傳播。當你將鵝卵石放入靜水中時，卵石附近的水顆粒會立即從它們的平衡位置移開。這些粒子的運動擾亂了相鄰的粒子，導致它們移動，并且該過程繼續，產生波浪。水波由沿著表面移動而遠離初始擾動的漣漪組成。各個水顆粒主要上下移動，略微側向運動。然而，所有粒子的累積效應產生的波從初始擾動點徑向向外移動。

具有與其他波唯一不同的性質的電磁波在傳輸線中受到關注。電磁波可以在沒有任何物質存在的情況下在真空中傳播。因此，印刷電路板上的銅和其中的電子都不需要移動以獲得到達目的地的瞬態信號。同樣，電磁波在真空中傳播的能力允許在外太空真空中與衛星進行通信。

一組稱為麥克斯韋方程的緊湊原理描述了電磁波現象。這些方程基于實驗觀察，并提供電場，電荷，電流和磁場的基本關系的最準確模型。這些方程涵蓋了無線電波，紅外線，可見光線，X射線和伽馬射線的整個電磁波譜。

電磁波傳播

電磁波由時變電場和磁場組成。當一對導體上的電荷改變時，電荷產生的電場改變。該時變電場產生磁場。時變磁場又產生電場。 （兩個帶電電極或變化的磁場可以產生電場。）這些時變場繼續在不斷擴展的區域中相互產生，并且產生的波從初始電荷變化的位置傳播。

圖9顯示了在傳輸線上傳播的電波和磁波。這些波是源處的正弦信號的結果。這些波處于橫向電磁（TEM）模式，因為場與行進方向垂直（橫向）。電（E）和磁（H）場也彼此垂直。

自由空間中的波傳播：

它所經過的介質的介電常數和磁導率決定了電磁波的傳播速度。

介電常數， ，是電介質在電場的影響下存儲電勢能的能力。自由空間的介電常數是

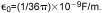
介電常數是電容器的重要參數。測量單元中法拉的存在應該有助于您記住定義，并將介電常數與滲透率區分開來。

滲透性μ是磁性物質的特性，其決定物質在物質占據的磁場區域中改變磁通量的程度。自由空間的滲透率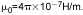

自由空間中的速度v是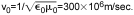

自由空間以外的材料中的波傳播：

雖然您可以將介電常數和滲透率表示為絕對數，但您幾乎總是將每個數量表示為相對值。相對值是您要表征的物質的介電常數或磁導率與相應的自由空間值之比。相對介電常數的另一個名稱是相對介電常數，或者更常見的是介電常數。表1顯示了各種材料的介電常數和相對滲透率。

皮膚效應：

對于諸如銅之類的良導體外的電場，導體表現出無限的導電性。但是，在完美的導體內部，不存在電場或磁場。在良導體內，變化的電場只能穿透薄的區域或皮膚。隨著信號頻率的增加，皮膚厚度減小。

計算趨膚深度的公式為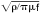，其中是以歐姆為單位的導體電阻率 - 米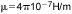，，f是以赫茲為單位的頻率。 （例如，銅的趨膚深度可能只有10μm。）

傳輸線上的波速：

表2顯示了使用傳輸線的電磁波速度各種電介質。

LUMPED-COMPONENT CIRCUIT MODELS

上述電磁波模型是物理學家為解釋實驗觀察而設計的最準確的模型。然而，對于習慣于包含集總元件的電路模型的電子工程師，例如電阻器，電容器和電感器，這些模型及其隨附的方程式是不方便的。集總元件電路模型的設計者只能處理直流和極低頻電流，但是工程師已經將這些模型用于表示傳輸線。

許多小的集總R，L和C分量代表傳輸線的連續均勻電阻，電感和電容。常規電流和電壓代表電磁波。圖10顯示了這個集總組件模型的兩個版本。二階傳輸線模型更準確，因為它包含所有三種組件類型。然而，工程師更經常使用一階模型，因為大多數傳輸線電纜和印制電路板導體的L值和C值使R值相形見絀。因此，忽略串聯電阻和分流電導通常是安全的。

電路模型的特征阻抗：

傳輸線的集總電路模型最重要的參數是特性阻抗，Z 0 。 Z 0 是源信號驅動器在信號高速轉換期間看到的有效傳輸線阻抗。在過渡結束后，電纜或印刷電路板導體的阻抗恢復到簡單電線的阻抗，每個電阻具有接近零的電阻。然而，傳輸線的最令人驚訝的方面是Z 0 ，即使電路模型由電感器和電容器組成，Z 0 實際上是一個沒有電抗元件的純電阻器。此外，與導體的串聯電阻不同，Z 0 的值不接近零。

在信號轉換期間，駕駛員看到只有Z 0 并且沒有看到負載阻抗，Z L ，它位于傳輸線的末端。

您可以從傳輸線電路模型中推導出Z 0 （圖11）。

本著微積分的精神，考慮傳輸線的短長度， x。量 V是串聯電感器的壓降，L。每單位長度的電壓，dV/dx = z * I，其中z是阻抗，I是電流。量 I是流過電容器的電流C，所以dI/dx5y * V，其中y是導納。導納，其單位是西門子，是阻抗的倒數。因此，您使用以下等式推導出Z 0 ：

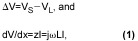
其中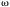 = 2pf，z =系列元素每單位長度的阻抗。

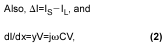
其中y =分流元件每單位長度的導納。

采用等式1的二階導數并代入公式2，公式2變為d 2 V/dx 2 = zXdI/dx = zyV，其解決方案

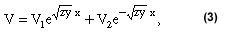
和

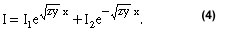
等式3是等式d 2 V/dx 2 = z * dI/dx = zyV，其中V是傳輸線上任何一點的電壓，當x接近零且V L = V 1 + V 2 。

當你將方程3和4替換為等式1和2并將它們組合起來，等式成為：

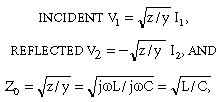
這是特征阻抗。

注意特性阻抗是一個完全獨立于頻率的純電阻，即使傳輸線電路由無功電感和電容元件。

導出的公式表示速度作為傳輸線的每單位長度的L和C的函數。速度= 1/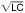。然而，通常，更容易從光速除以相對介電常數的平方根導出速度。您可以更容易地獲得的值，而不是確定傳輸線的每單位長度的L和C.

物理尺寸的特征阻抗：

因為傳輸線的電感和電容僅取決于實現的物理特性，您還可以從線路的物理尺寸推導出傳輸線的特征阻抗。圖12顯示了三個配置示例。微帶傳輸線的典型尺寸為：對于1盎司銅，T（導體厚度）= 0.0015英寸，對于G-10玻璃環氧樹脂，H（基板厚度）= 0.062英寸，W（導體寬度）= 0.015英寸。

傳輸線上的多個負載：

傳輸線上的大多數學術教科書都假設每條傳輸線只有一個負載，但許多印刷電路板在一條傳輸線上放置多個負載。因此，實踐工程師已經開發出一種經驗公式來修改特征阻抗和信號速度，以解決多個負載增加的額外電容。公式如下：

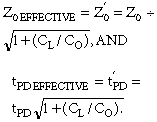
C 0 是傳輸線每單位長度的空載電容，C L 是每單位長度增加的負載電容。增加的電容會降低有效Z 0 并增加傳播延遲。雖然這些公式不在理論教科書中，但它們在許多應用筆記中，包括一個經典的摩托羅拉MECL（摩托羅拉發射極耦合邏輯）手冊。本手冊也是微帶傳輸線的C 0 值的來源。

對帶有開路負載的傳輸線的反思：

接下來是對從信號源到開路負載端的傳輸線上傳播的信號波的啟發式描述，其中信號反射回源。圖13中的集總元件電路模型使用均勻分布的電感和電容，它們看起來像許多無窮小的集總元件。電壓和電流定義信號。

當信號到達傳輸線的負載端時，其有序進展被中斷。在時間t 1 ，波正接近負載端。信號能量波的電壓和電流一起前進：L Y 正在傳輸電流，但L Z 不是，并且C Y 向E收費，但C Z 不是。在C Y 之間存在電壓，因此電流立即開始流過L Z 。因為L Z 攜帶與L Y 一樣多的電流，所以C Y 增加不超過E.當前進入L Z 流入C Z ，將其充電到E.在時間t 2 ，能量波到達終點。現在所有電容器都充電到E，所有電感器現在都帶有電流I.

此時，波浪的進展無法繼續。 L Z 正在向C Z 傳送電流，但C 之外沒有電感id =“id6040672-329-sub”> Z 充當電流的出口，因為C Z 變為充電。當C Z 變得過度充電時，您可以在時間t 3 看到結果。 L Z 在排出磁能之前不能停止傳送電流。 L Z 繼續將電流驅動到C Z ，直到C Z 的電壓為2E。此時，L Z 中的電流為零。在時間t 4 ，當L Z 停止傳送電流時，所有電流L Y 進位被驅動到C Y ，加倍C Y 并強制L Y 中的電流停止。

同時，電壓在L Z 的兩端變得相等，所以C Z 上的過充電無法逃脫。 C Y 和C Z 的電壓為2E，L Y 且L Z 為零。假設每個L的能量等于每個C的能量，該過程沿著該線逐漸地繼續。結果是幅度為E的電壓波返回到源并且增加到原始波。反射電流波表現為負I波返回光源并消除原始波，因此凈電流為零。沒有電流流回源，但波前確實傳播。從光源流出的電流繼續這樣做，直到它遇到反射波。

請記住，這種解釋僅僅是用最初用于低頻的集總元件模擬實驗數據（現實）的嘗試。電路。您可以使用電磁波微分方程或波動方程和邊界條件更準確地模擬這些現象。

對具有短路負載的傳輸線的反思：

短路反射負載與上述類似，電壓和電流波形互換。

對具有匹配負載阻抗的傳輸線的反射：

當負載阻抗等于傳輸線的特征阻抗時，不會發生反射。負載看起來像傳輸線的均勻特征阻抗，因此負載吸收所有的波能。通常，這種配置是理想的。此外，通常，當負載阻抗與傳輸線的特征阻抗（Z 0 ）不匹配時，應添加Z 0 端接電阻與負載并聯。負載阻抗通常很高，因此其值無關緊要。由于源阻抗通常較低，因此可以將一個終端電阻與源串聯，這樣總電阻等于Z 0 。在應用這些指南時要小心，因為會發生異常。

對具有不連續或中間負載的傳輸線的反射：

不連續性（均勻特征阻抗的變化）或中間負載在傳輸線上產生反射，就像負載端的阻抗不匹配一樣。任何中間反射都會返回光源并增加傳輸線上傳輸的其他波。

對任何負載阻抗的傳輸線的反射：

如果負載阻抗Z L ，則與傳輸線的Z 0匹配并且如果Z L 既不是零也不是無窮大，負載不吸收的信號能量反射回源。當反射到達源時，如果源阻抗Z S ，則不匹配Z 0 ，從源回到負載有一個反射。反射一直持續到傳輸線上的負載，源和損耗完全吸收波的能量。

的下列公式確定傳輸線不匹配時的反射大小結束（源或負載）：

此公式用于負載不匹配。如果用Z S 代替Z L ，則可以使用公式作為源端。對于開路計算，將公式除以Z L 以避免無窮大超出無窮大。

格點圖：

您可以使用晶格圖來計算反射（圖14）。首先，請注意，V S 時的初始源電壓V 0 為0.5V因為1V的電壓V在Z S 和Z 0 之間劃分。晶格圖顯示在t = 0時，V 0 = 0.5V電壓波傳播到負載端，其中反射系數為0.6。因此，在t = 1時的負載下的總電壓V L 是0.8V。然后0.3V的反射電壓在0.5V入射波上返回光源。當0.3V波到達源時，不會發生反射，因為Z S = Z 0 ，使反射系數為零。

Bergeron圖：

您可以使用更復雜的Bergeron繪圖技術計算反射（圖15）。該技術對非線性終端特別有用;也就是說，根據信號電平是高電平還是低電平，驅動器或接收器具有不同的阻抗。

階梯步進反射：

圖16是傳輸線的示例其源極和負載阻抗產生反射，導致電壓以階梯方式上升。當Z S 且Z L 僅略高于Z 0 。第一個信號波是完整驅動信號的一部分，因為驅動信號在Z S 和Z 之間劃分0 。接收器上的信號在達到其全值之前需要大約四次反復往返（40 nsec）。

振鈴反射：

圖17提供了產生反射的源阻抗，傳輸線和負載的不同配置示例，這些反射在傳輸線上顯示為振鈴。過沖可能會損壞接收器電路，或者如果接收器在振鈴消退之前讀取信號，則會破壞數據。圖中的波形只有方形邊緣而不是曲線，因為它來自模擬。在該模擬中，Z L >> Z 0 。隨著負載和電纜損耗逐漸吸收信號的能量，振鈴衰減。您現在可以看到t RISE ＆amp; 2次飛行時間和互連長度> 0.1波長的標準不是絕對分界，而是經驗法則，因為阻抗不匹配和反射的影響本質上是模擬的。

工商管理碩士學位，并且是IEEE的成員。他在工作之外的活動包括全球旅行，攝影和育兒。