前面,我們講了機械臂的運動學(kinematics)(點擊藍字查看):正向運動學和反向運動學。
正向運動學指的是在已知機械臂各個關節角度的情況下,推算end-effector(機械臂終端)的位置和方向(合稱pose)。反向運動學指的是在已知end-effector的位置和方向,推算各個機械臂的關節角度。我們主要研究反向運動學。
讓我們看一下基于反向運動學的控制邏輯圖:

在給出機械臂的end-effector的pose后,反運動學模塊計算出各個關節所需要的角度,然后通過電機產生力矩(torque)去執行。在此期間,通過反饋(feedback)去消除一些控制誤差。
但是,事實上會有很多的干擾因素存在。例如:
地球引力(gravity)
慣量(inertia)
摩擦力(friction)
科里奧利力和離心力(Coriolis and centrifugal)
由于連桿之間是通過關節(joint)耦合在一起,連桿之間會有反作用力和反向慣量
以及一些人為的要求,例如:
我們想要機械臂運動的速度,按照我們預先的設定運行(velocity and acceleration)
我們想要求機械臂在觸碰外物時候做出安全保護(external force)
這些我們暫且稱之為disturbance(干擾),當然有些“干擾”是我們故意要求的,比如說需要按照預設軌跡的速度運行。加入“干擾”后的示意圖如下:
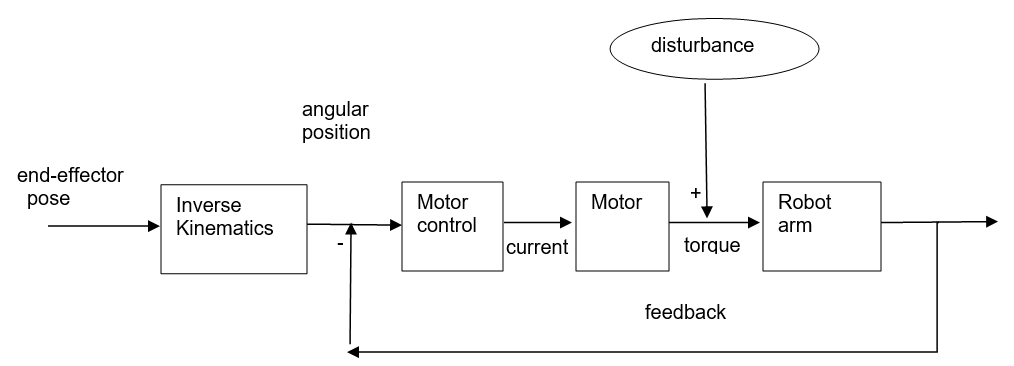
如果我們能提前計算出來這些“disturbance”,然后在控制環路中將它“抵消”(有時候也叫前饋控制)。這樣,就能使得機械臂“完美”運行了。讓我們再改一下控制邏輯圖:
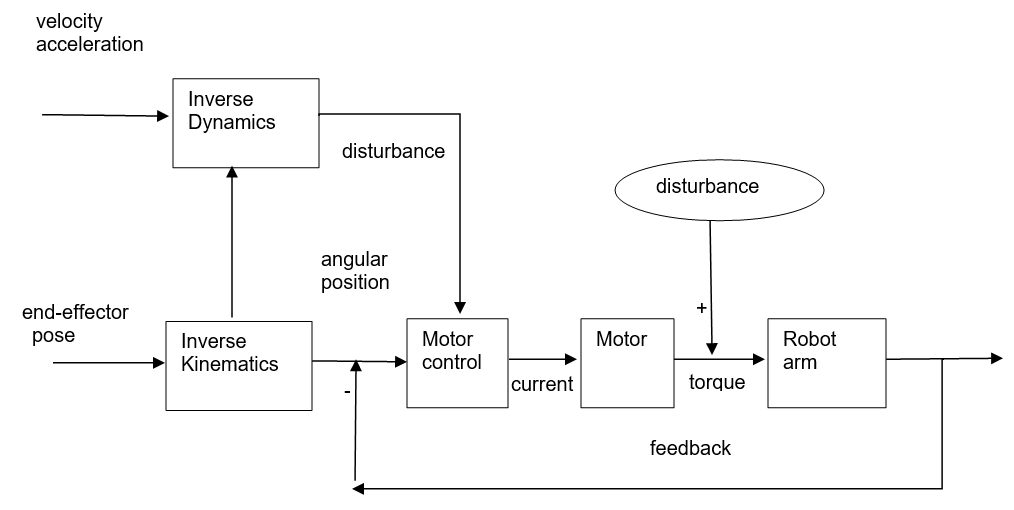
為了計算這些“disturbance”。我們需要考慮幾個因素:
機械臂各個關節角度,即q
機械臂各個關節的速度,即qd(對q求導)
機械臂的各個關節的加速度,即qdd(對qd再次求導)
機械臂的質量和各個連桿的重心點
有了這些因素,我們可以通過數學方法:
u=M(q)qdd + C(q,qd)qd +G(q)
求出所需要的力矩,其中M項代表克服了機械臂的加速度慣量以及不同連桿之間的慣量影響所需力矩、C項代表了克服科里奧利力和離心力所需力矩、G項代表了克服地球引力力矩。
其中Inverse Dynamics叫做反向動力學,它的作用是輸入想要的關節速度(qd)、關節加速度(qdd)、關節角度(q),輸出為每個關節所需要的力矩(u)。當然也有正向動力學(forward dynamics),它的作用和反向動力學相反,輸入關節角度(q)、關節速度(qd)、每個關節的力矩(u),輸出為每個關節的加速度(qdd)。
上述的控制邏輯圖,是一個“前饋控制”的例子,它的作用是預先計算出所需的力矩,輸入給控制器,“反饋”的存在是為了消除一些誤差,例如摩擦力和其他噪音。
總之,我們需要這么一個“動力學”模型,使得我們可以抵消各種不同的“disturbance”的影響 --- 慣量、地球引力、科里奧利力和離心力等等。另外,實際電機的功率是有限的,通過反向動力學我們也可以準確知道電機需要提供多少力矩,從而為電機選型提供參考依據。
下圖初略表示了end-effector – inverse kinematics – inverse dynamics之間的關系:
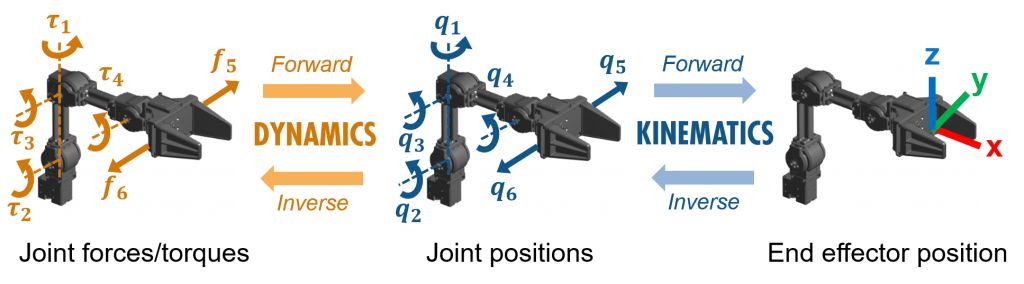
Robotics System Toolbox(RST)中的動力學算法
RST 提供了動力學方面的函數和Simulink block。
MATLAB函數:
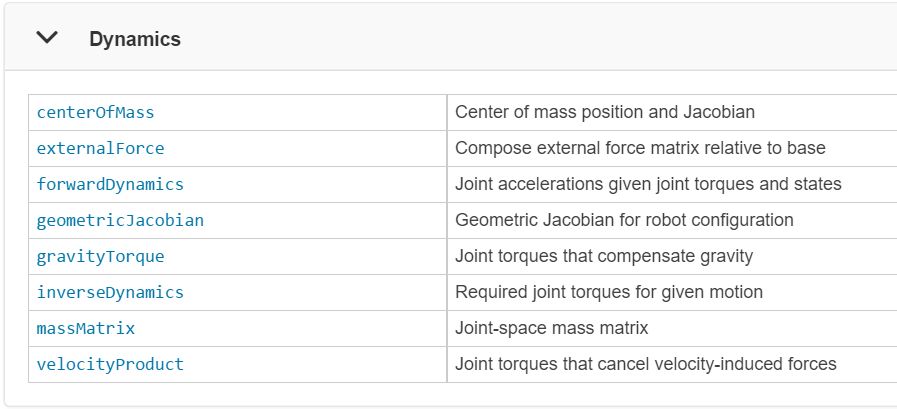
Simulink blocks:
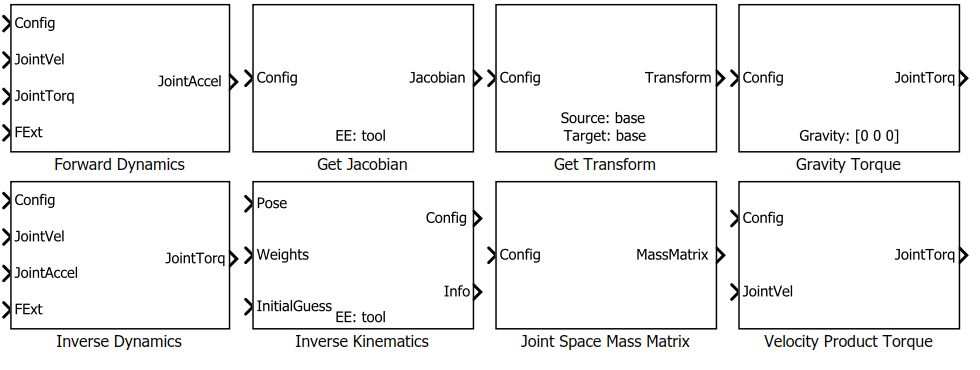
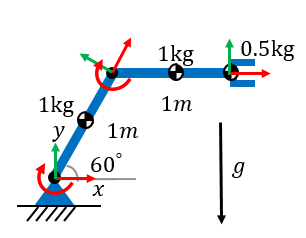
讓我們看一個簡單的例子:
這是一個工作在2D空間的機器人。標明了各個結構件的質量、長度和重心。在靜止狀態下,兩個關節分別需要多大的力矩去抵消地球引力并支撐起這個機器人?
我們先一步步地構造這個機器人:
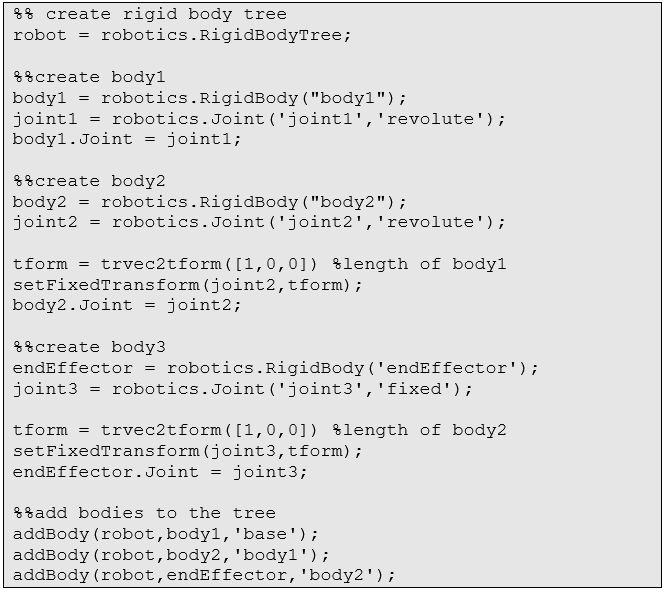
然后加入重心、質量:

然后在速度和加速度都是0的情況下,調用inverse Dynamics函數算出力矩:

tau =
20 10
很明顯,第一個關節要比第二個需要更大的力矩。
我們也可以用gravityTorque這個函數試一下,結果是相同的。

gravTorq =
20 10
如果我們將速度或者加速度改變一下,看看力矩的變化,例如:
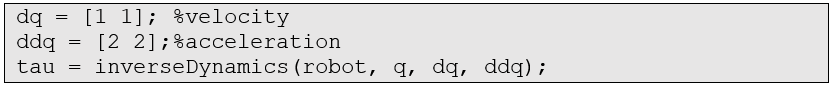
相應地,所需力矩也增大了。
tau =
30.5981 12.1340
Simulink 示例
在MATLAB Central File Exchange上搜索“Designing Robot Manipulator Algorithms”。
這是一個機械臂按運動軌跡抓取物體的例子:
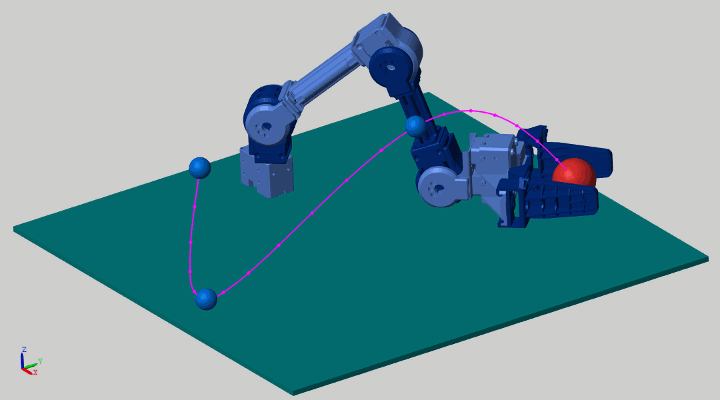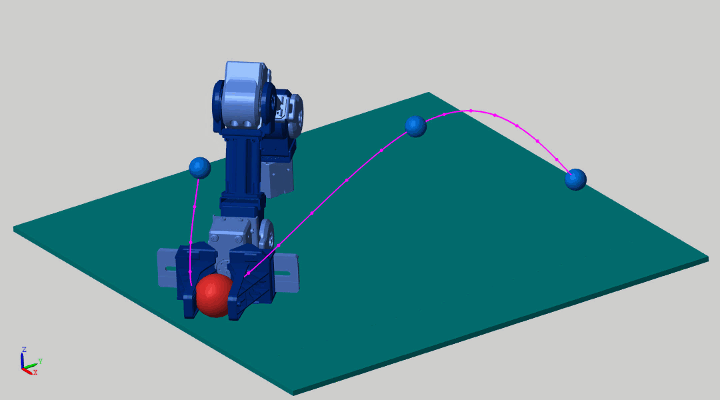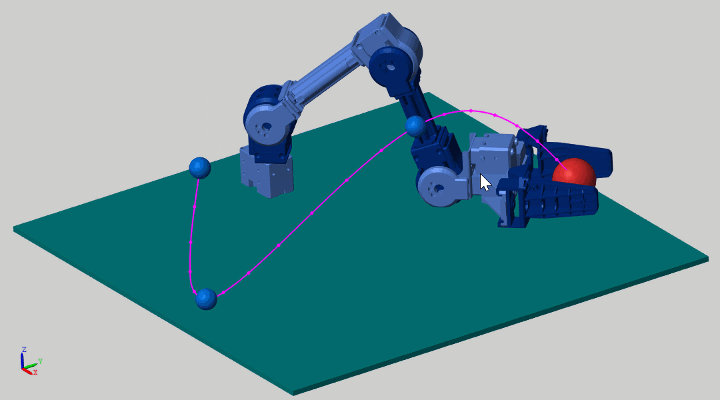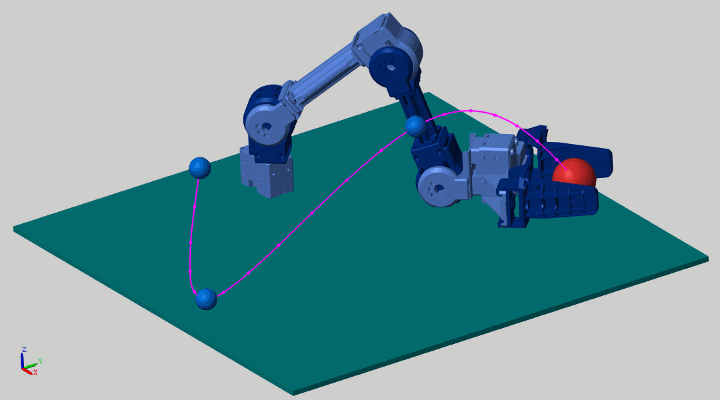
在前面運動學算法中,我們也介紹了這個例子。當時我們用反向運動學(inverse kinematics)去計算end-effector的位置。這次我們用力矩控制的方式來重新看一下這個問題。這里有兩種方式供參考:
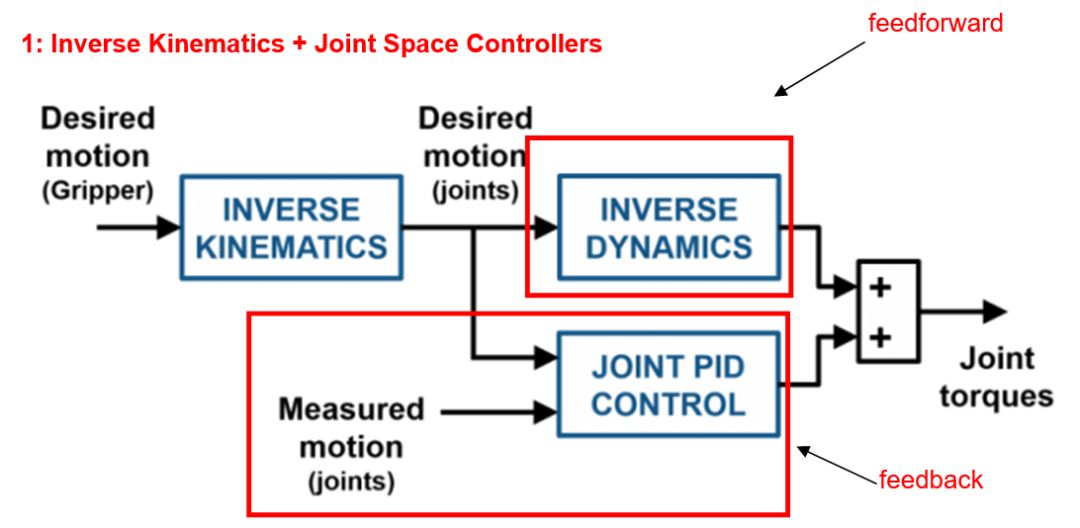
首先,inverse kinematics根據end-effector的位置,計算出各個關節(電機)所需要的角度位置,然后交給各個關節的電機去執行。由于關節控制的是角度。所以叫Joint Space Control (即關節角度控制)。
前饋部分(feedforward)負責計算出所需力矩(用來抵消重力,按預定軌跡運動等等)。
反饋部分(feedback)用PID去消除誤差。
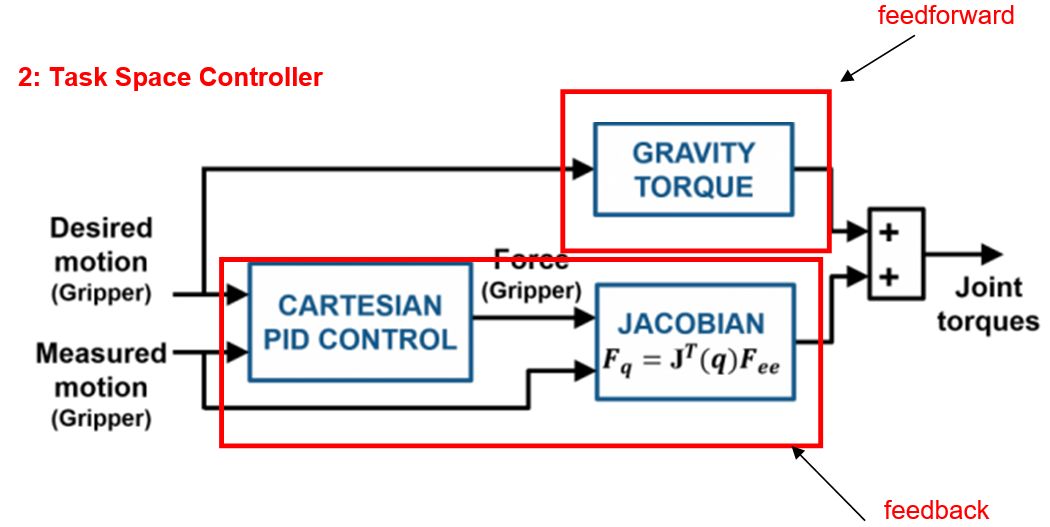
這個做法是直接控制end-effector的位置,并用PID去消除end-effector的位置誤差。也叫做task space control,即直接控制在XYZ空間(也叫笛卡爾坐標的位置)。
前饋部分只做一件事:計算抵消地球引力的力矩。
反饋部分用PID去控制end-effector的位置。然后用Jacobian矩陣將end-effector(在笛卡爾坐標)的力矩,轉化成各個關節的力矩。
Computed Torque Control
有了機械臂的動力學模型(dynamic model),我們可以應用的控制方法有很多種。通常來說,反饋是必要的 – 可以消除控制誤差和一些噪音。從力矩計算的角度來看,可以做:
力矩前饋控制。剛才兩個例子都是將計算好的力矩做前饋。由于機械臂的移動速率遠遠小于電機控制速率,所以計算力矩的頻率并不高。比如說,電機的控制頻率為5K Hz,前饋力矩計算的頻率大約是50Hz。對控制器的硬件要求不高。
計算力矩控制(computed torque control)。computed torque control工作在較高的控制頻率上(例如1K Hz),要比力矩前饋控制頻率高的多。對控制器硬件要求較高。
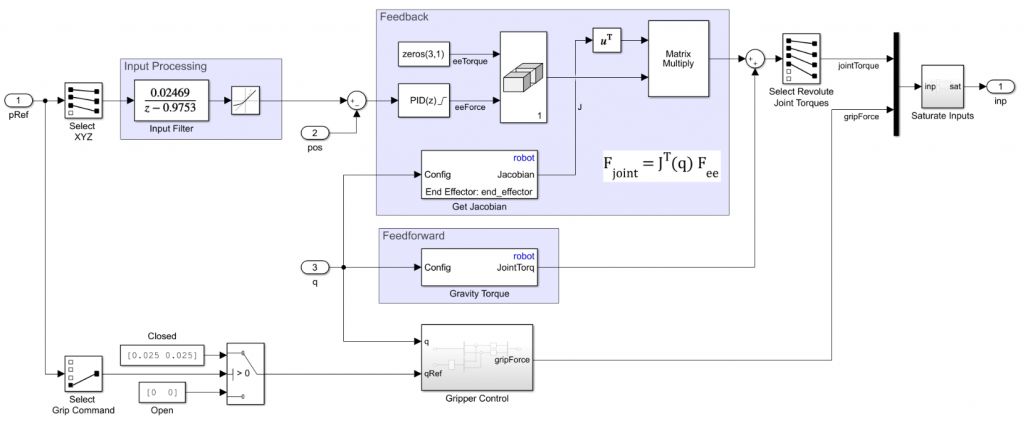
Simulink提供dynamics方面的blocks,可以方便地搭出computed torque controller:
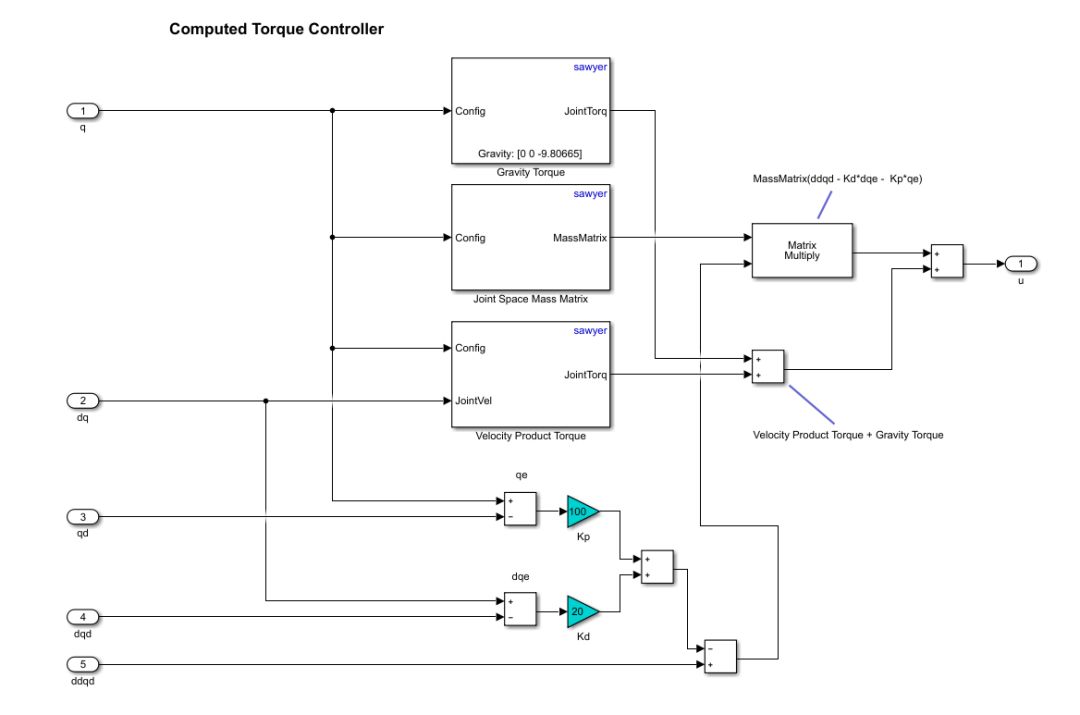
computed torque controller的輸入:
q,機械臂關節角度
qd,預設的機械臂關節要達到的角度 (desired q)
dq,機械臂關節速度,即對q求導
dqd,預設的機械臂關節要達到的速度 (desired)
ddqd,預設的機械臂關節要達到的加速度 (desired )
computed torque controller的輸出:
u,機械臂各個關節的力矩
有了computed torque controller我可以做出比較復雜的控制系統,例如一方面要求機械臂按預定的trajectory(含角度、速度、加速度等信息)運行;一方面又要求機械臂遭受外力干擾后改變運行軌跡(trajectory)。
如果感興趣,可以看MATLAB自帶的“Perform Safe Trajectory Tracking Control Using Robotics Manipulator Blocks”這個例子。機械臂在碰到遮擋的硬物,改變預設的運行軌跡,保證運行安全。

-
控制器
+關注
關注
112文章
16416瀏覽量
178762 -
電機
+關注
關注
142文章
9050瀏覽量
145908 -
動力學
+關注
關注
0文章
105瀏覽量
16994
發布評論請先 登錄
相關推薦
深度解析!RK3568 加持機械臂是如何實現顏色識別與抓取的?

機械臂的高效運作,連接器起關鍵作用
【原創】 drawbot 平面機械臂scara寫字畫畫機器人DIY教程貼
OrangePi AIpro應用:機械臂應用開發指南

工業機器人和機械臂的設計、功能和應用有哪些區別?
奧比中光推出2.0版大模型機械臂
大象機器人開源協作機械臂機械臂接入GPT4o大模型!

國產Cortex-A55人工智能教學實驗箱_基于Python機械臂跳舞實驗案例分享
基于六維力傳感器的機械臂自動裝配應用

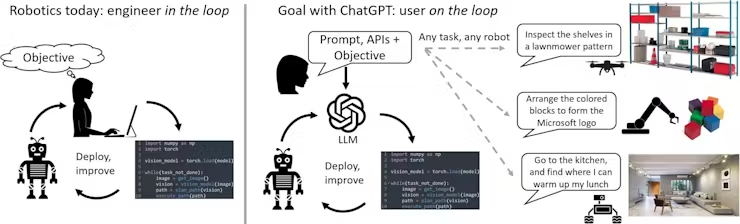
自然語言控制機械臂:ChatGPT與機器人技術的融合創新(下)

機械臂技術的前沿探索:年度案例回顧!
【國產FPGA+OMAPL138開發板體驗】(原創)2.手把手玩轉游戲機械臂
使用ChatGPT學習大象機器人六軸協作機械臂mechArm!





 關于MATLAB 中的機械臂算法分析和介紹
關于MATLAB 中的機械臂算法分析和介紹










評論