鋰電池是目前在各個能源密集型行業中用途廣泛,例如新能源汽車、電力微網、航空航天等。電池模型的建立對研究電池的特性、SOC(state-of-charge)估計、SOH(state-of-health)估計、BMS算法開發以及電池系統的快速實時仿真有重要的意義。
等效電路建模,由于其簡單適用性,常常應用在在系統級仿真和控制算法設計過程中。通過實驗數據采集、等效電路模型建立和數學優化技術,用相對簡單的RC等效電路可以模擬一個電芯。若干電芯模型通過不同類型的并串聯方法,形成電池包模型。在電池包模型內,也可加入熱電效應仿真。

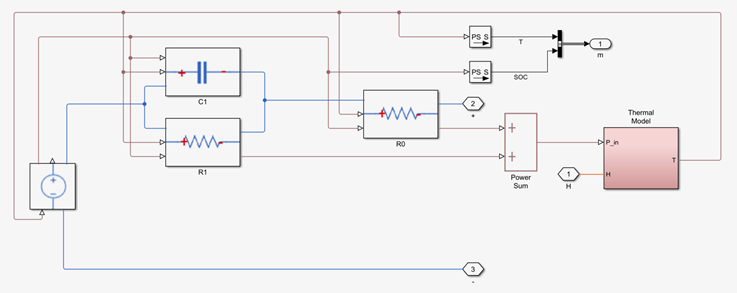
在上圖中,10 個電芯以 10S1P 的形式形成一個電池包(此處工具為 Simscape)。藍色的線表示電線連接,橙色的表示熱交換連接。在圖中電芯之間的熱交換形式為熱對流。
電芯的模型為下圖所示:R0 表示內阻,R1C1 表示一對 RC,左邊的電壓源表示開路電壓(Em)。由于只有一對 RC,所以這是一階等效電路。
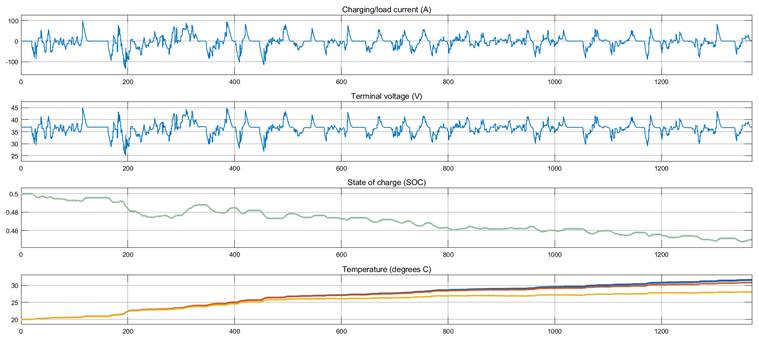
上圖表明,通過在一個不斷充放電的工況下的仿真,我們發現電芯 5 和電芯 6 有較高的溫度,而電芯 1 和電芯 10 溫度較低。原因是在串聯結構中,位置處于中間的電芯散熱較差,而處于邊緣的電芯散熱較好。
鋰電池的型號多種多樣,比如鎳鈷錳三元材料 (NMC)、磷酸鐵鋰 (LFP) 等。每種電池的化學特征決定了各自不同的等效電路特征。等效電路的特征由如下兩個要點決定:
RC 的階數
R0 、RC 和 Em 的數值
下一節中我們將討論如何獲取(估計)上述兩個要點數值。
鋰電池的老化對模型的影響也是電池模型研究的方向之一。找出模型的拓撲結構和模型參數的改變趨勢,對于 SOH 的估計有很強的現實意義。本文將在第四章中討論電池老化對電池模型的影響。
被動均衡也是電池管理系統(BMS)的研究熱點之一,文末我們將給出一個被動均衡的示例供讀者參考。
RC 等效電路的參數設計
脈沖放電法
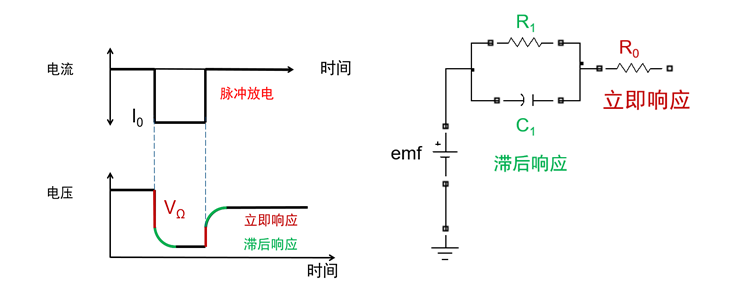
RC 等效電路有物理意義的前提是電路中所有 RC 對和 R0 都必須完整地“經歷過”一個放電周期。 右下圖所示的 RC 等效模型中,R0 表示一個放電循環中的“立即響應”,RC 對表示一個放電循環中的“滯后相應”。左下圖表示脈沖放電以及開路電壓(Em)的回穩過程。 可以看到,在一個脈沖放電后,電芯通過“立即相應”和“滯后響應”再靜置一段時間后得到的穩定的開路電壓。通常來說靜置時間為 1 小時以上為佳。
脈沖放電的一個脈沖使得 10%(一個比較合適的百分比)的 SOC 下降,靜置等待開路電壓回穩。此處,10% SOC 的下降為一個估計值,假設一個電池容量為 100mAH,那么我們放電 10% 即 10mAH,如果放電倍率為 1C,分 10 次放完。那么單個脈沖放電時間為 1 小時 * 10% = 6 分鐘。
如此重復多次(避免 SOC 為極限低點而損害電池),得到完整的脈沖放電曲線,我們就可以得出 RC 對、R0 和 Em 估計所需要的實驗數據。
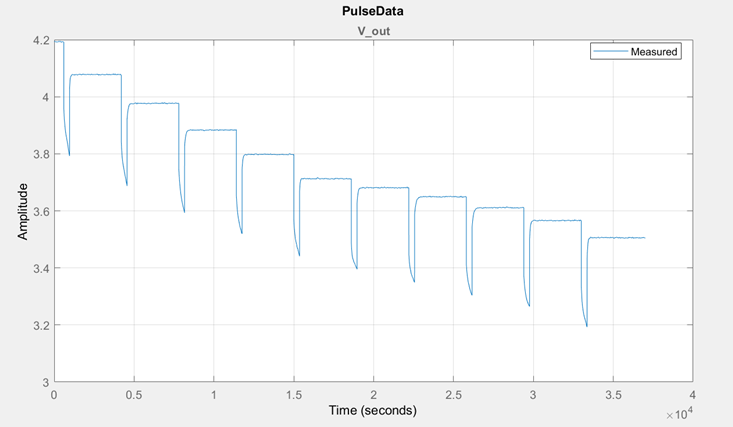
在某一溫度下完整的放電曲線
由于鋰電池對溫度敏感,上述放電實驗可以在多個溫度下進行。加入溫度的影響后,建模的任務就是要根據多個溫度下放電數據,估計出 R0,RC 和 Em。它們在模型的表現形式均是一個二維的 Look-Up Table。
R0, R1, C1, Em = f(SoC, T)
電池模型參數估計的步驟
步驟一:確定RC 階數
很多人理解為,RC 階數越多越準確。這個是錯誤的觀點,因為過多的 RC 階數會讓數學優化過程變得計算量過大;也有可能會造成過擬合現象,即將數據中的噪聲數據也擬合出來。這樣的數學模型沒有意義。
正確的 RC 階數取決于:放電靜置回穩后的那段指數曲線。

由于 RC 之積 Tau 的單位為時間。線段的長度為時間。該線段的函數表達式為:

如果為一個三階函數,我們可以用 MATLAB 的曲線擬合工具箱去擬合:
y = 1c - a*exp(-b*x) - d*exp(-e*x) - f*exp(-g*x)
有了這個基本思路,我們就可以從一階開始逐步用 MATLAB 做曲線擬合,直至符合要求為止。
步驟二:構建參數估計模型(基于某一溫度)
根據上一小節的原則確定模型階數以后,我們可以用 Simulink/Simscape 來構建電芯參數估計模型。此處 C1、R1、R0、Em 都是基于 SOC 的 Look-Up Table。
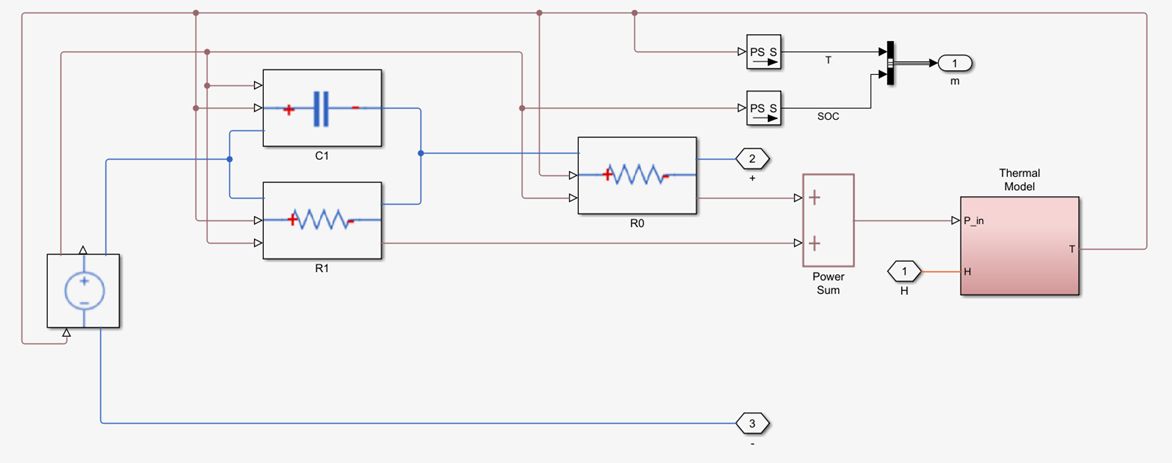
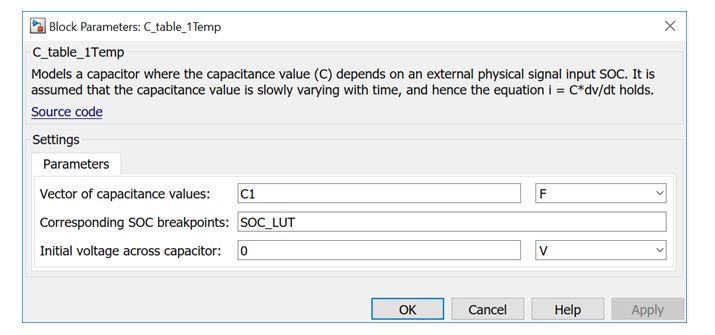
步驟三:參數估計和驗證
參數估計的輸入為某一溫度下的放電數據,輸出為 Em、RC、R0 等參數的 Look-Up Table(一維)。
Simulink Design Optimization 可以根據輸入數據,選擇不同的算法進行參數估計,目的是仿真曲線和實驗曲線誤差最小。
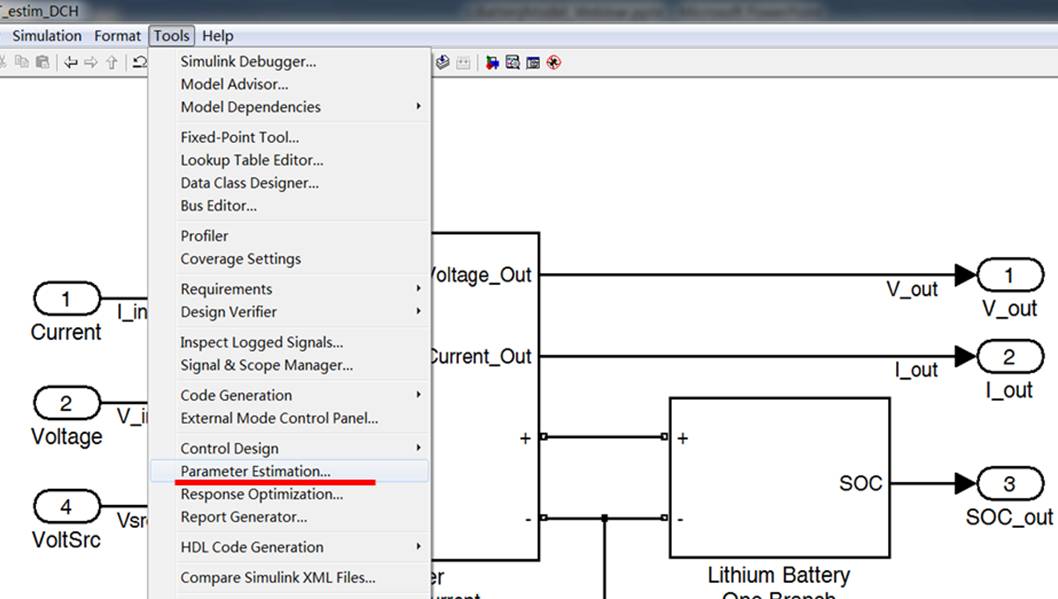
參數估計有幾種優化算法可選:
Gradient descent
Non-linear least squares
Pattern search
Simplex search
其中 Non-linear least squares 比較常用,但容易找到非全局優化點。Pattern search 為全局優化,適合初學者。
在參數估計結束之后,可以做實際工況數據對模型的驗證工作。所謂驗證就是用實際的電池運行數據(同一溫度下)來校驗得到的等效模型。如果誤差很小,那么表示該模型真實可用。例如:下圖的黃色(仿真)和紫色(實測)的數據基本一致。
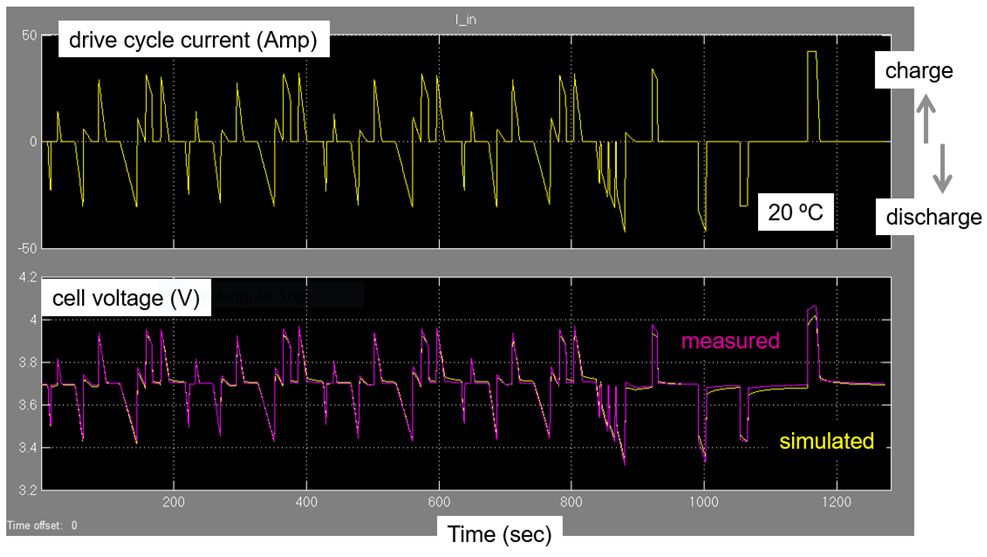
很多人抱怨在參數估計中由于計算量過大,導致運行速度很慢,這里給出兩個小技巧可顯著加快估計速度:
選擇并行多核加速
打開“Fast Restart”開關
步驟四:在多個溫度下建立電芯模型
剛才我們的等效電路模型中,RC、R0、Em 等經過參數估計,得出的實際上是一維的 Look-Up Table(維度為SOC),那么我們可以通過設計多個溫度下(例如 5、20、40 攝氏度)的:
脈沖放電實驗
參數估計
將“溫度”這個緯度加入到等效電路中,最終形成二維的 Look-Up Table。即完整的具有溫度和 SOC 屬性的電芯模型。
R0, R1, C1, Em = f(SoC, T)
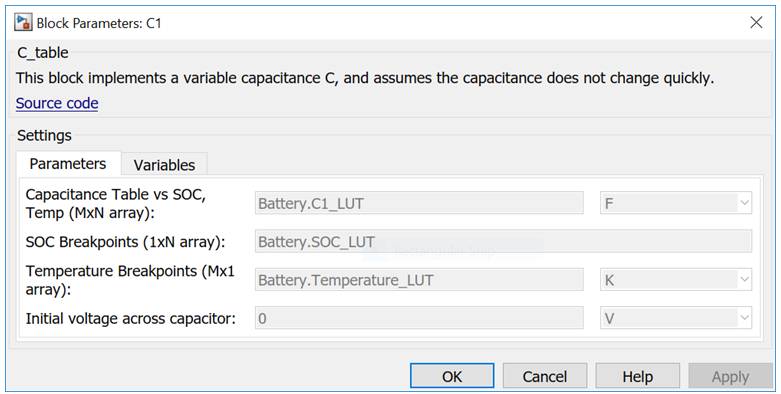
步驟五:形成電池包模型
在單個電芯模型建立完成后,可通過不同的串并聯線路將電芯形成電池包模型。電池包模型可以用來仿真熱效應、電芯均衡或者其他應用場景。
電池老化對電池模型的影響
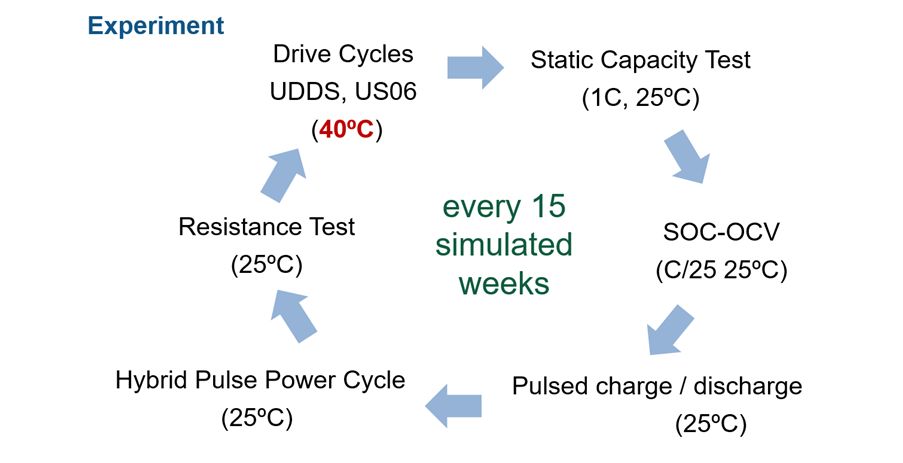
老化對電池的影響不可忽視,老化的影響應該被反映到電池模型。為了研究這一課題,MathWorks 和其他廠商的工程師設計了為期 13 個月的老化實驗:
為了加速老化過程,工程師選擇在 40 度的溫度下做 UDDS 的駕駛循環測試,每隔 15 星期記錄下變化的數據,并做等效模型的建立和參數估計,試圖通過這一過程發現模型拓撲和參數變化的規律。
電路拓撲的變化
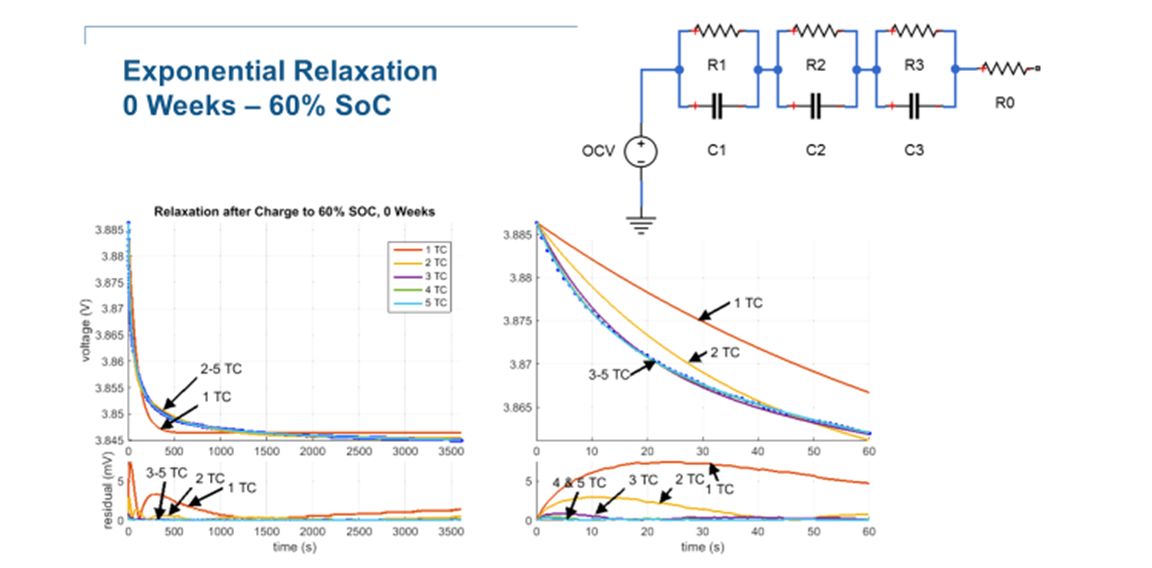
0 周時候的電路拓撲
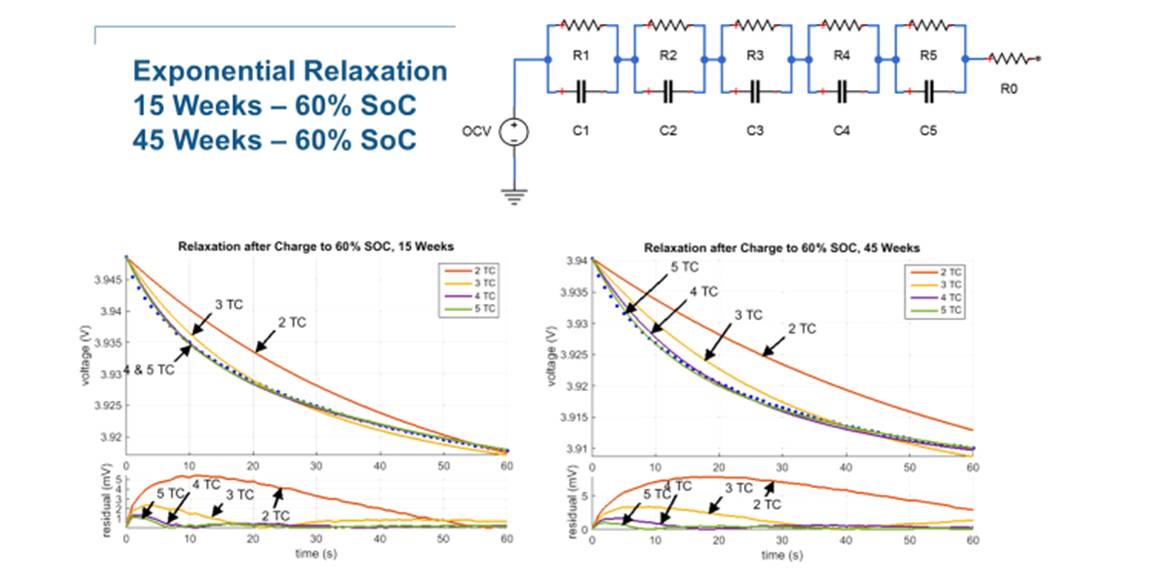
15、45 周時候的電路拓撲
實驗顯示:在電池未老化的時候(0 周),用 3 階等效電路模型可以反映電池特性。
在電池老化后期,用 5 階等效電路模型可以反映電池特性。
電池參數的變化
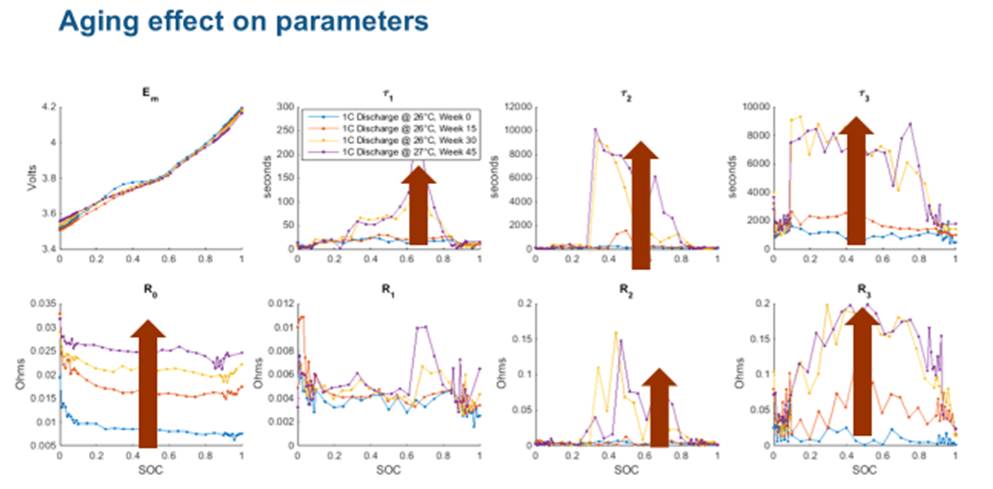
實驗顯示,電池老化對等效電路參數的影響為:
開路電壓不變
R0 變化很大
RC 對數增加
Tau 增加(趨于穩態時間增長)
BMS 設計者如果能在控制器中建立一個內部的電池模型,通過參數規律和數值的估計,將有助于 SOH 的估計策略。
被動均衡模型示例
均衡策略是 BMS 的一部分,目前實際應用較多的是被動均衡策略。
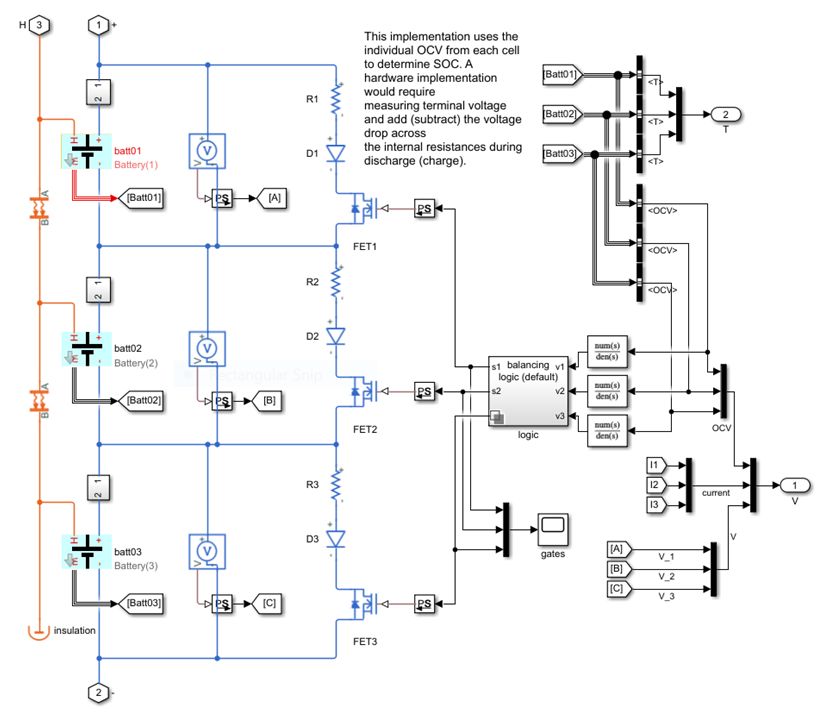
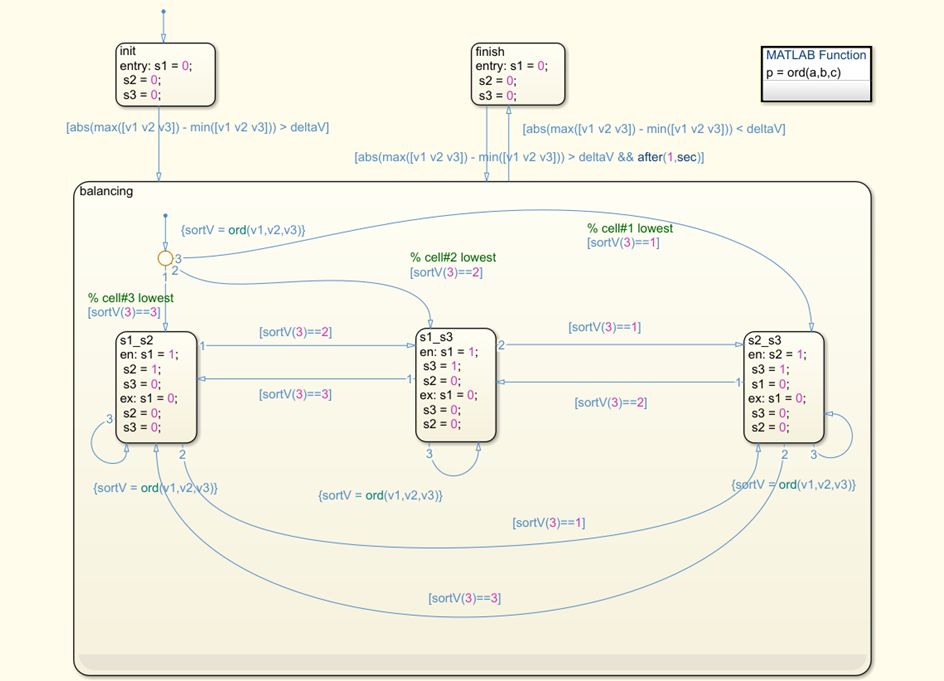
上圖給出了一個被動均衡的示例模型,三個電芯組成的電池包在狀態機(Stateflow)的邏輯驅動下控制 MOSFET 電路開關對各個電芯進行電壓均衡。
MathWorks有能力為廣大電池(或 BMS)企業提供各種咨詢服務,咨詢服務可包括:BMS 開發 MBD 咨詢、電池模型建立咨詢、流程改進咨詢(以 ISO26262 為例)。
-
鋰電池
+關注
關注
260文章
8147瀏覽量
170894 -
芯片
+關注
關注
456文章
51010瀏覽量
425278 -
等效電路
+關注
關注
6文章
292瀏覽量
32796
發布評論請先 登錄
相關推薦




 關于利用MATLAB/Simulink 鋰電池建模的步驟分析
關于利用MATLAB/Simulink 鋰電池建模的步驟分析












評論