雖然ASIC公司和“良好的工程實踐”強調同步設計技術,但時鐘速度的增加使用速度高達50至200 MHz,這迫使設計人員實施異步邏輯電路。不幸的是,雖然大多數數字設計工程師都熟悉組合和同步時序邏輯電路,但異步時序邏輯設計的世界仍然模糊不清。過渡地圖可以指導設計人員通過這個不熟悉的世界來實現可靠的異步設計。旅程從一些基本概念和定義開始。數字電路可以分為組合電路或順序電路。組合電路是那些輸出值完全取決于輸入信號電平的電路。順序電路的輸出值和當前狀態值不僅取決于當前輸入值,還取決于電路的先前狀態。您可以將時序電路分為兩種類型:同步和異步。在同步電路中,當前狀態在時鐘的邊沿上變化(圖1 a)。異步電路中的當前狀態在一個或多個輸入變量的轉換之后發生變化,然后是電路的傳播延遲周期(t pd )。

圖1同步(a)和異步(b)電路的行為設計模型幾乎相同。主要區別在于異步電路依賴于傳播延遲來達到當前狀態值。
創建順序異步邏輯電路時,請注意電路中的傳播延遲。否則,可能發生不希望的輸出毛刺或甚至永久的不希望的狀態。為避免異步電路的危險,設計人員更多地選擇同步實現。然而,同步電路也存在固有問題。設計人員必須將輸入信號與狀態機時鐘同步,以避免亞穩態。此外,輸入值的變化僅在同步時鐘發生之后影響輸出值,增加了電路響應所需的時間(即延遲)。時鐘延遲和輸入信號同步的需要會嚴重降低系統的性能。
圖1 b是異步順序狀態機的框圖模型。該模型由一個組合邏輯塊組成,其輸出信號決定了下一個狀態值。塊的輸入變量是外部輸入信號和當前狀態變量。該模型假設組合邏輯沒有傳播延遲,并且當前狀態變量在建立時間之后采用下一狀態變量的值。建立時間等于真實組合邏輯塊中可能出現的最長傳播延遲(t pd )。
當電路穩定時(定義為在等于或長于t pd 的時間段內保持相同的變量),當前和下一狀態變量具有相同的值。然而,有時,狀態變量在當前狀態和下一狀態變量達到穩定狀態之前呈現幾個中間值。這些中間值表示不穩定狀態,其中輸出變量值對于給定的輸入值組合保持變化。在極端情況下,電路會振蕩。
由于通過電路的各種信號路徑具有不同的傳播延遲,因此兩個或多個輸入信號的同時變化可能會導致不可預測的狀態轉換。因此,為了避免不受控制的行為,設計應該一次只允許一個輸入變量。此外,連續輸入信號變化之間的時間間隔應該比達到穩定狀態所需的時間長。當強制執行這些限制時,電路以“基本模式”運行。
電路實現可能允許兩個或多個狀態變量由于輸入信號轉換而同時發生變化。這種電路具有競爭條件,電路行為取決于哪個狀態變量變化最快。如果在幾次臨時狀態轉換后電路達到的穩定狀態是相同的,無論哪個狀態變量更快,電路都有非關鍵的比賽。如果最終狀態不同,則該賽道有重要的比賽。良好的設計必須在基本模式下運行,避免關鍵競爭條件。
鎖存器保持當前狀態值
在同步狀態機中,觸發器是保存當前狀態值的存儲器元素。在異步狀態機中,存儲器單元是鎖存器;圖2顯示了這樣的鎖存電路。產品術語(A& B)稱為START術語。當該項為真時,輸出Z為真。產品項(B& Z),其中一個輸入變量是來自輸出的反饋,稱為HOLD項。一旦START為真,長于t pd ,只要HOLD項保持為真,輸出Z就會保持設置。
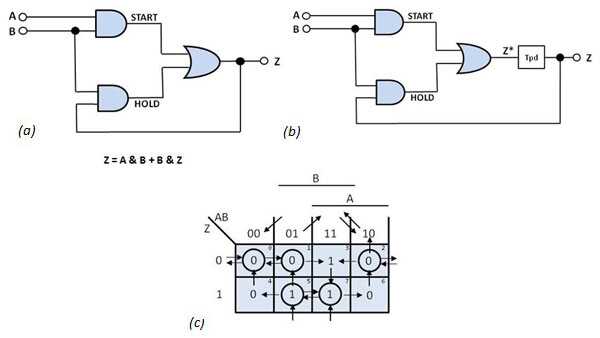
圖2鎖存電路(a)是異步狀態機的存儲元件。鎖存器的異步模型(b)和轉換映射(c)提供了對電路行為的深入了解。
圖2 b說明了異步鎖存器的模型。假設原始門具有零延遲并且組合電路(Z *)的輸出是下一狀態變量。輸出Z在通過電路等于傳播延遲(t pd )的時間之后取值Z *。下一狀態變量Z *可以表示為布爾方程:Z *(t)= A& B + B& Z(t)。輸出Z(當前狀態變量)是Z(t + t pd )= Z *(t)。除了塊延遲之外,該電路模型可以作為組合邏輯進行分析;因此,您可以使用稱為轉換映射的卡諾圖類型來研究其行為。圖2 c顯示了鎖存模型的轉換映射。
轉換映射的每一列代表外部輸入變量的組合,每行代表一個組合現狀變量。這些組合被安排成使得相鄰的行或列的差異僅在于一個變量的變化。由行和列定義的方塊包含電路的相應下一狀態值(Z *)。在圖2中,因為A和B是外部輸入變量而Z是唯一的當前狀態變量,所以你需要確定這個鎖存器的行為是一個映射四列兩行。
此映射包含許多參考標記,有助于理解相應電路的行為。在每個輸入變量名稱下面有一個水平條,它覆蓋變量為true的那些方塊。正方形的角落有數字,方便參考。地圖頂部列之間的傾斜箭頭表示Z-的電平轉換 - 如果有的話 - 由于輸入轉換。
如果將電路的總狀態定義為輸入和當前狀態變量的當前組合,過渡圖的每個方格與電路的總狀態具有唯一的對應關系。在地圖內從正方形移動到正方形對應于電路總狀態的變化。當電路到達其下一狀態值與其各自的行值一致的方形時,電路已達到穩定狀態。過渡圖顯示了圈出的所有穩定狀態。其余的方塊表示不穩定狀態。
轉換映射跟蹤電路變化
此時,請注意異步電路的狀態幾乎在外部輸入改變后立即改變,而不是像在同步電路中那樣跟隨時鐘的邊沿。在使用轉換映射分析異步電路的行為時,請記住,當輸入變量發生變化時,電路的狀態變化對應于表示新輸入組合的列的立即水平過渡。如果下一狀態Z *的新值與當前狀態Z一致,則新狀態是穩定的。否則,垂直轉換隨后發生,直到電路達到Z * = Z的狀態。
分析圖2 c中的映射,其中說明這種行為。假設輸入和輸出變量值分別為AB = 00和Z = 0;然后,square 0表示電路的狀態,并給出下一個狀態值Z * = 0。由于Z *和Z相同,因此輸出保持穩定。如果B變為“1”,則當前狀態仍為“0”,盡管方形1表示總狀態。如果A現在變為“1”,則下一狀態Z *變為“1”并且不再等于Z.電路狀態移至平方3.該狀態不穩定,迫使鎖存器狀態垂直移動到穩定狀態狀態為7,因為AB保持為“11”。以類似的方式,每次輸入值改變時分析鎖存器的下一個狀態。
分析也適用于具有多個狀態的電路 - 記憶元素。圖3 a顯示了一個邏輯圖,您可以通過檢查圖3中相應的布爾方程和卡諾圖來推導出span> b 。轉換圖圖3 c,是兩個卡諾圖的組合,通過連接Z *和Q的相應值形成*。地圖頂部的值表示電路輸入變量A和B的當前值。地圖左側的值表示電路的當前狀態值(ZQ)。穩定狀態,正方形具有下一州的價值es與相應的行值重合,用圓圈表示。
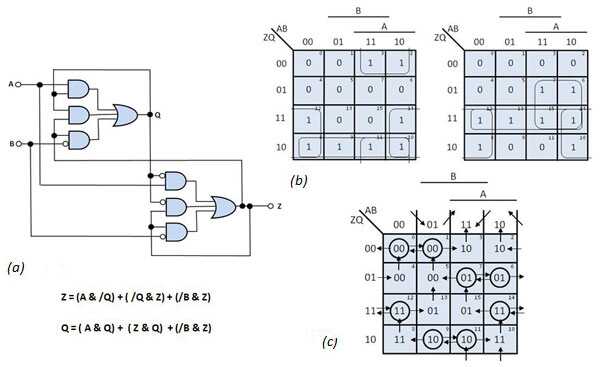
圖3從該采樣電路的邏輯圖(a)中,您可以導出卡諾圖(b)中的下一狀態變量Z *和Q *。組合這些映射會產生電路的轉換映射(c)。
假設系統以對應于平方1(ABZQ = 0100)的狀態啟動。如果A然后變為“1”,則總狀態移動到方形3,其顯示下一個狀態“10”。方形3的狀態不穩定,因為ZQ和Z * Q *不同。因此,電路狀態移動到方形11,其中下一個狀態是“10”。這是穩定狀態(ABZQ = 1110),因為當前狀態和下一狀態是相同的。電路保持穩定狀態(ABZQ = 1110)。
如果B然后變為“0”,則系統移動到方形10,顯示下一個狀態“11 “因為這種狀態不穩定,系統狀態在方形14處移動到穩定狀態(ABZQ = 1011)。同樣,您可以繼續分析轉換圖的其余部分。參見圖3 c用于所有可能的轉換。
對于此電路,每次A置位,Z置位,當B置位時,Z復位。此行為描述了置位/復位翻轉的特性-flop,其輸出取決于輸入邊沿轉換。
地圖圖表競爭條件
轉換圖提供了一種有價值的工具,用于分析競爭條件,當兩個或多個下一個狀態因輸入值轉換而同時發生變化時會發生競爭條件。以下示例有助于說明轉換映射作為分析工具的用處:
案例1:在圖4 a的電路,假設初始狀態(ABZQ = 1101)。當轉換圖(圖4 b)表示時,當前狀態變量ZQ和下一狀態變量Z * Q *是“01”。如果輸入變量A變為“0”(AB = 01),則下一狀態Z * Q *變為10. Z和Q同時變化,這將設置競爭條件。如果路徑延遲Z和Q相等,電路經歷以下轉換:01-> 10-> 00。
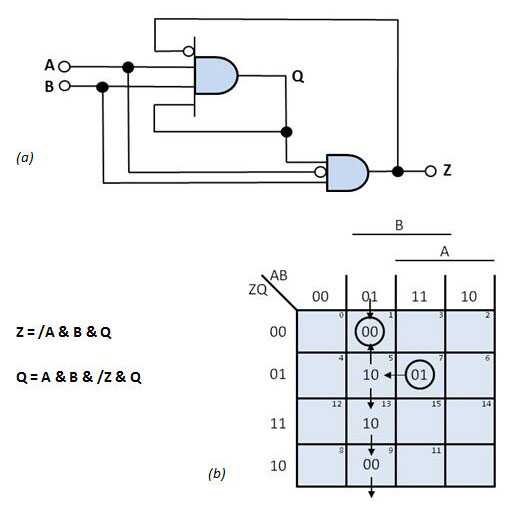
圖4案例1:該電路(a)包含非關鍵競爭條件。如果電路在穩態ABZQ = 1101上電,則它可以以兩種方式響應A中的負轉變。如轉換圖(b)所示,兩個響應都達到相同的結束狀態。然而,穩定所需的時間隨路徑而變化。
因為Z和Q的路徑延遲通常不同,但是從01到10的過渡不會直接發生,而是由兩個中的一個發生。潛在序列:01-> 11-> 10-> 00或01-> 00。在這個例子中,電路在任何一種情況下達到相同的穩定狀態“00”,這說明了一個非關鍵的競賽。然而,在最終狀態下穩定所需的時間仍然不確定,因為它取決于路徑延遲。
案例2:在圖5 a的電路中,假設起始狀態為( ABZQ = 1101)。如圖中的映射所示,當A變為“0”時,以下序列是可能的:01-> 10-> 00,01-> 00或01-> 11。因此,兩個不同最終的穩定狀態可以用于輸入轉換。這是關鍵競賽的一個例子。應該避免具有關鍵競賽的電路設計,因為轉換的結果是不可預測的。
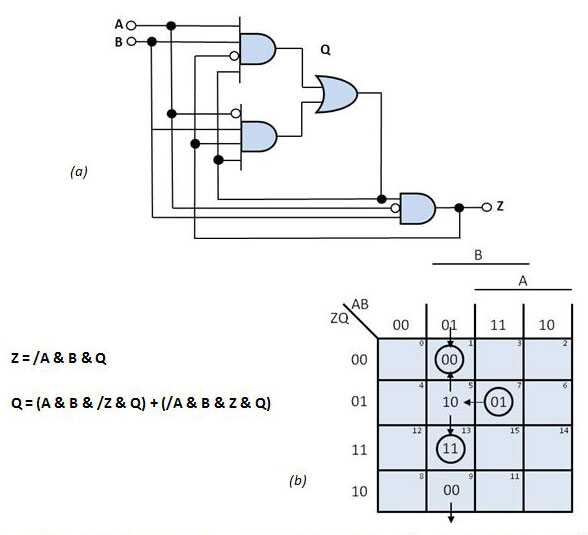
圖5案例2:該電路(a)包含嚴重的競爭條件。如轉換圖(b)所示,電路可以在A變化后穩定在兩種穩定狀態之一。電路到達的狀態取決于哪個邏輯塊更快。
案例3:圖6a 和過渡圖中的邏輯圖(圖6 > b)對應于不穩定的電路。當AB從11變為01時,ZQ無限期地在不穩定狀態“01”和“11”之間轉換,即,輸出Z振蕩達AB = 01。在穩定電路的映射中避免這種行為。
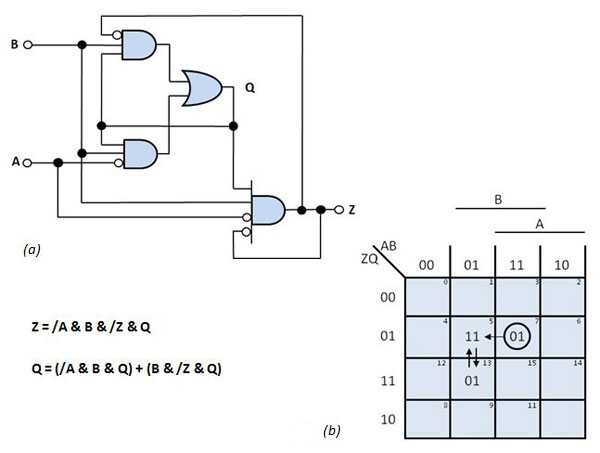
圖6情況3:該電路(a)振蕩時輸入變量AB從AB = 11變為AB = 01。轉換圖(b)清楚地顯示了危險。
通過分析這三種情況,很明顯,為了正確操作和預測電路行為,有必要確保只有一個下一狀態變量對于任何給定的輸入轉換都會發生變化。
使用地圖計劃設計
轉換圖不僅可用于分析異步電路,還可用于合成設計。例如,考慮設計一個電路,當B為高電平時,其輸出Z跟隨A的轉換,當B為低電平時,電路保持穩定。對于任何給定的AB值組合,輸出Z可以是“0”或“1”。該電路不能是簡單的組合邏輯。它必須是順序的,因為輸出值取決于當前輸入的值和先前的狀態。這種電路的時序圖出現在圖7 a中。
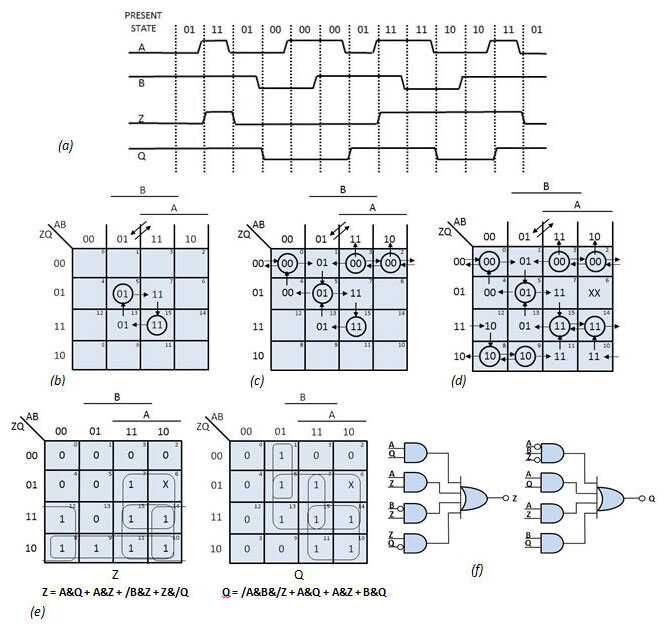
圖7建議電路的時序圖(a)顯示,當B = 1時,Z跟隨A,如果B = 0,則Z保持不變。為電路創建轉換圖(b)從假設的穩定狀態開始,并用所需的下一狀態值填充相鄰的正方形,同時避免狀態沖突(c)。最終的狀態圖(d)構成了卡諾圖(e)的基礎,從中可以得出最終的電路(f)。
設計這個電路的第一步是繪制轉換圖,假設您可以使用2狀態變量狀態機實現該電路。輸出Z是當前狀態變量之一; Q是第二個現狀變量。由于電路具有兩個輸入變量和兩個當前狀態變量,因此轉換映射包含16個方塊(圖7 b)。每個方塊標識輸入和當前狀態變量的一個組合。
過渡圖上方的箭頭表示Z的所需過渡。如圖所示,當B為“1”時,Z的變化遵循A的過渡。即,當Z從“01”變為“11”時,如果Z不是“1”,則Z從“0”變為“1”。如果Z,則Z從“1”變為“0”。當AB從“11”變為“01”時,該值不是“0”。沒有其他輸入轉換會導致Z改變。
第二步是用適當的下一狀態變量Z * Q *的值填充方塊。請記住,Z *和Q *分別是在通過電路的傳播延遲之后Z和Q所采用的值。 Z *和Q *實際上是虛擬變量,有助于理解電路的過渡行為; Z *和Q *沒有物理現實。
按照以下幾條規則填寫過渡地圖:
1。每次輸入變量改變時,電路立即水平轉換到標識新輸入組合的列;即水平轉換表示輸入變化。
2。如果新的下一狀態值與行值一致,則電路已達到穩定狀態。
3。如果新狀態不穩定,則電路在同一列內移動,直到下一個和當前狀態變量相同。垂直轉換表示輸出變化。每個垂直狀態轉換需要一個傳播延遲,因此,為了最大化電路性能,您的設計應該在達到穩定狀態之前具有最小數量的垂直狀態轉換。
4。為了避免競爭條件,只有一個下一狀態變量應該作為狀態轉換的結果而改變。
開始填充地圖(圖7 b),假設電路處于方形5(ABZQ = 0101)指示的狀態,并且系統在該位置穩定。因為這表示穩定狀態,所以下一狀態等于當前狀態,因此您可以在方塊中寫入“01”并在其周圍畫一個圓圈。
如果A現在變為“1”, Z也應為“1”,因為B = 1。電路水平轉移一個方格到右方到方形7,在那里你寫“11”,顯示Z的變化,而Q保持不變。在這種狀態下,Z * Q * = 11與ZQ = 01不匹配;因此,電路垂直移動(保持AB = 11)至方形15,其中ZQ = 11。在這個方塊中,電路達到穩定狀態,所以你可以寫“11”并圈出它。
如果A再次從“1”變為“0”,“Z應該是”0 “新的下一個狀態是”01“。現在,電路水平轉換到13號方,你寫”01“。因為Z * Q * = 01且ZQ = 11,所以該狀態不穩定。因此,電路垂直移動到方形5,這是原始的穩定狀態(ABZQ = 0101)。
到目前為止,電路符合要求,Z的值跟蹤A的轉換而B為真。剩下的要求是當B為假(B = 0)時Z不會改變。同樣,從方形5開始(圖7 c),當B從“1”變為“0”時,電路水平移動到方形4。 Z不應該改變,但你可能想要用新的總狀態來識別這種轉變。因此,切換Q的值,并在方形4處寫入“00”。這是一個不穩定的狀態,因此電路移動到方形0(ABZQ = 0000),在那里它將達到穩定狀態,因為Z * Q * = ZQ = 00。寫“00”,并在方塊0處圈出。
避免狀態沖突
如果A現在從“0”變為“1”,則“Z”應保持為“0” '因為B = 0(請記住,只有當B為高電平時,Z才會跟隨A的變化。)電路水平移動到方形2(ABZQ = 1000),在那里達到穩定狀態。用“00”填充這個方格,然后圈出來。如果B現在變為“1”,則電路在方形3(ABZQ = 1100)處移動到穩定狀態,因此用“00”填充該方塊并將其圈起來。如果A現在變為“0”,則Z保持為“0”,電路狀態變為平方1.
此時,為Q分配值“0”或“1”。你將Q指定為“0”,Z * Q * = ZQ = 00,并且電路將在方形1處達到穩定狀態。然而,這種狀態分配存在一個問題:如果A隨后從“0”變為“1”,然后Z應該從“0”移動到“1”,這將迫使方形3包含10作為其下一個狀態。因為方形3的下一個狀態已經是“00”,所以在方形1處賦值Q = 0導致狀態沖突。
要避免狀態沖突,必須在方形1(圖7 c)中指定Q = 1。當方形1處的“01”時,狀態不穩定并且電路狀態垂直移動到方形5(狀態ABZQ = 0101)。以類似的方式,通過其余狀態來完成地圖(圖7 d)。
示例在方塊5中的起始值是任意的。因此,轉換映射中給定函數的狀態賦值可能會有所不同,具體取決于初始選擇并不總是有效。碰撞的發生可能會迫使您從不同的初始穩定狀態重新啟動轉換映射狀態分配。練習最終會產生最佳狀態分配的直觀知識,在達到穩定狀態并消除所有潛在碰撞之前最小化轉換次數。
一旦填寫轉換圖,合成設計的第三步是從轉換圖生成卡諾圖。每個next-state條目的第一個值對應于Z的值;第二個對應于Q的值。圖7 e顯示了該例子的卡諾圖。
治療不在乎
從這些地圖中推斷出相應的布爾方程。選擇公式的乘積項時,請注意避免出現輸出毛刺的電路。避免此類危害的經驗法則是指定足夠的產品術語以涵蓋所有細節,并添加冗余的產品術語,以便相鄰的產品術語重疊。
同樣,您需要對待“不關心” (X)仔細。為它們分配有助于簡化產品術語的值。然后,將這些值恢復到轉換映射,并驗證分配不會產生潛在的電路振蕩,例如那些情況3 指示。
在圖7 d中,square 6有一個不關心下一個狀態。圖7 e中的布爾方程假設方形6中Z * = 1且Q * = 1.如果在上電期間,電路進入對應的狀態方波6(ABZQ = 1001),下一個狀態為“11”,電路進入穩態ABZQ = 1011(方形14)。
設計綜合的第四步(也是最后一步)是繪制Z和Q的邏輯圖。如圖7 f中的邏輯圖所示,該實現包括2級門電路。這種類型的架構非常便于PAL實現和ASIC應用;它可以讓您構建方便的專用模塊,傳播延遲最小。當前狀態變量Z是電路的實際輸出,Q是輔助變量。回想一下,Z *和Q *是虛構變量,代表異步電路模型中的下一狀態值。當前狀態變量Z和Q是物理存在且出現在電路邏輯圖中的唯一變量。
通過使用更復雜和正式的程序,轉換圖分析可以處理具有三個或更多外部輸入變量的電路。這種情況超出了本文的范圍,但是,這提供了對異步電路的概念性理解。通常,同步電路可能更容易理解和設計。然而,當速度是高優先級時,異步邏輯就是答案。過渡地圖分析可以指導您實現可靠的實施。
-
電路設計
+關注
關注
6678文章
2457瀏覽量
204745 -
PCB打樣
+關注
關注
17文章
2968瀏覽量
21746 -
華強PCB
+關注
關注
8文章
1831瀏覽量
27819 -
華強pcb線路板打樣
+關注
關注
5文章
14629瀏覽量
43091
發布評論請先 登錄
相關推薦
如何設計自動駕駛系統的狀態機
Verilog狀態機+設計實例
如何寫好狀態機
使用ModelSim自動生成狀態機FSM的狀態轉換圖
什么是狀態機?狀態機5要素
狀態模式(狀態機)





 如何設計轉換映射指導成功的異步狀態機
如何設計轉換映射指導成功的異步狀態機











評論