1、特性阻抗

在直流或低頻時，各器件或各設備之間互相連接時，隨意拉兩根線就行了。當頻率高到長度與波長可比時，就要用同軸線或雙絞線連接了。而且連接時要采用連接器，否則會造成失配甚至亂輻射以致不能正常工作。傳輸線是用來傳輸的，要不輻射，最簡單的方法就是加個屏蔽套，做成屏蔽線。尺寸均勻，做成同軸狀的傳輸線稱為同軸線，內充介質便于彎曲的同軸線稱為同軸電纜或射頻電纜。

電波在同軸線內傳輸時，必須尺寸均勻才能順暢，否則會產生反射。因此同軸線互連

時有個規格或參數問題，必須參數相同才行；這個參數就是特性阻抗ZC，有時也寫成Z0.

習慣上Z0表示50Ω，而ZC泛指特性阻抗。無窮長的同軸線纜肯定是沒有反射的，這時他的輸入阻抗稱為特性阻抗。

一段線輸出端接上一個負載，假如輸入端沒有反射的話，這個負載的阻抗就是這段線的特性阻抗。特性阻抗是一個由尺寸與介質決定的電參數，同軸線的特性阻抗公式為：

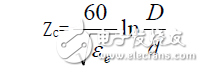
（式中εe為同軸線內充填介質的有效介電常數，D 為外導體內徑，d 為內導體外徑。）

2、反射系數、回損、駐波比

一段線接上輸入阻抗為特性阻抗的負載是沒有反射的，這種負載稱為終端負載或精密負載。以它為參考，通常認為它的反射為零。假如一段線接上其它不匹配的負載ZL，必然有反射。這個反射必然正比于兩者的差異，這就出現了反射系數Г這樣一個參數。

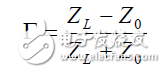
反射系數它是反映負載特性的最原始的參數，要想反射系數小一些，只要負載ZL接近特性阻抗Z0即可。雖然Г是個最原始的參數，也是測量出的參數，但由于是復數，一般人并不習慣用它。習慣上描述不匹配的程度常用回損RL，或駐波比SWR。

返回損失（回損）= 20logΓdB ，由于Γ≤1，一般為負值，但習慣上不講負號。

駐波比，這是一個天饋線中最常見的一個技術指標，英文縮寫為S.W.R，也有用V.S.W.R，即強調是電壓之比。

線上電壓因反射的存在而出現有高有低的現象并不是我們希望的，我們希望|Г|→0，也就是ρ→1。

3、史密斯圓圖

為了便于形象化的理解阻抗情況與匹配的過程，作些簡單的計算時，采用圓圖就非常方便了。

1）反射系數同心圓（等|Г|圓或等ρ圓）

對于某一傳輸線端接任一負載的情況下，可用它的Г值來表示，不管你的負載為何值，它必然落在|Г|=1的圓內。

讓我們畫一個半徑為1的圓，則圓心代表反射為零的點，過零點畫一根水平線，左右兩交點分別代表Г= -1（即∠180°）與Г=1，則任意一段傳輸線上的任一點，都可以在圓內找到其對應的|Г|∠ф。將直徑等分即得如下圖所示的等反射圓。

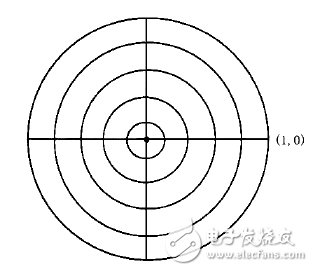
（等|Г|圓或等ρ圓）

在一根傳輸線上移動時，其|Г|值是不變的，只是相位隨距離而變，正好在等|Г

圓上轉。看這個圖時請注意，相位為-2lβ，即l越長，相位越落后，因此圖上l的方向是順時針方向。另外還有一個2倍，即轉角快了一倍；如l=λ/2，在圓上就轉了360°，仍在原地。

此圖一般是用等駐波比畫的，不如等|Γ|均勻等距好畫。半徑表示|Г|（或ρ），越靠近圓心反射越小。假如將半徑分成十等分， 畫上十個同心圓，則圓圖類似于打靶用的靶。

2）等阻圓與等抗圓

圓圖的制作上有這樣一個要求，那就是要用歸一化阻抗，即z=Z/Z0，對于50Ω的同軸線，50Ω負載的歸一化阻抗為1。用小寫字母表示歸一值：由下式可以簡化得到等阻圓和等抗圓。

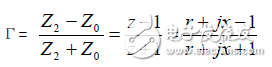
等阻圓為一偏心圓族，圓心在，半徑為。

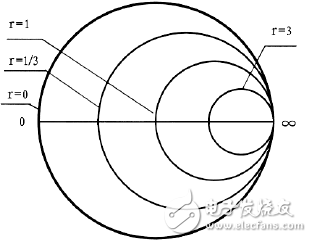
（等阻圓）

等抗圓圓心在，半徑為的圓族，上面為正，下面為負。

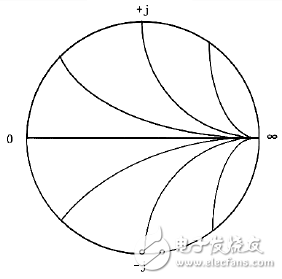
（等抗圓）

3）阻抗圓圖

將三種圓畫在一起就成了史密斯圓圖，也常稱阻抗圓圖，或簡作圓圖。通常它是用來表示傳輸線上的輸入阻抗的，水平軸為實數軸，上半面偏電感，下半面偏電容，右面（嚴格講來是在r=1的圓內）阻值偏高，左面（在r=1的圓外）阻值偏低，因此將負載頻響特性畫在圓圖上那情況將是一目了然的，該采取什么措施，也是一清二楚的。

阻抗圓圖上適于作串聯運算，若要作并聯運算時，就要轉成導納，在圓圖上這非常容易，某一點的反對稱點即其導納。

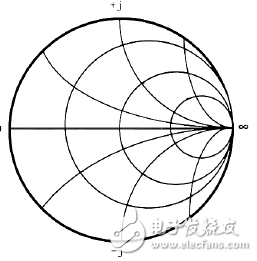
（史密斯圓圖）

作阻抗運算時圖上即阻抗，當要找某點的導納值時，可由該點的矢徑轉180°即得；此時圓圖所示值即全部成導納。

另外注意一點，不管它是負載端還是源端，只要我們向里面看，它就是負載端，永遠按離開負載方向為正轉圓圖，不要用源端作參考。

有人說圓圖是微波技術上的一個重大發明，的確，史密斯將R+jX會出現的四個∞(+jx,-jx,r,｜Z｜)縮為圓上的一個點；而且極坐標上相位是連續的，比用直角坐標好；Γ為線性的同心圓坐標，形象的描述了傳輸線上的輸入阻抗軌跡。在圓圖上阻抗與導納是兼容的。圓圖作為輸入阻抗特性的表征，用作簡單的單節匹配計算是非常有用的，非常直觀，把復雜的運算用簡單的形象表現出來，概念清楚。

注：當在圓圖上用歸一化阻抗表示時(這是規定),某點的輸入阻抗在經過λ/4后即成為該點的導納.這是因為經λ/4線后的Z2變成Z1，而Z1Z2=Z02,在用歸一化表達后z1z2=1，所以z1= 1/z2 = y2 。

4.參考面概念

要建立一個概念,那就是傳輸線上每點的輸入阻抗都是不同的。也就是說輸入阻抗是位置坐標的函數,同時也是頻率的函數；只有Z2=Z0這一點除外,而這一點通常是作不到的.因此談輸入阻抗時必須說明是哪一點的 ,或者說參考面設在何處。

如一條線上只有一個產生反射的點,或者說產生最大反射的點,則參考面應當取在該點,這樣該采取什么措施就一目了然了.假如參考面差得太遠,此時各測試點連成的軌跡呈盤香狀.這時就得考慮移參（儀器上的移動參考面功能，簡作移參）了。

輸入阻抗（或導納）在圓圖上是變的，它的軌跡就是等|Г| 或等駐波比圓；也就是說，無耗傳輸線反射系數的幅值是不變的，或者說駐波比是不變的，只是相位在變；因此通常用駐波比ρ來對天饋線提要求，是很自然的。因為這樣做既簡單又明了，比對輸入阻抗提要求方便多了。但是若要進行阻抗匹配工作，就得用輸入阻抗了，否則就太盲目了。

用圓圖來表示反射的性質，或描繪整個匹配過程，那是最明確不過的了。而且用作匹配時，該采取什么措施也可說是一目了然的。另外圓圖還可用來做簡單計算。

5.相位量φ簡單介紹

相位是一個時間上的量，它是描述正弦信號的一個參量。式中ω為角頻率（實質為角速率），φ0為初相。

V=Vmsinφ=Vmsin(ωt+φ0)=Vmsin(2πft+φ0)

當線上為純行波時，由于波行進需要時間，就會產生相位延遲(時)t = x/c,由t造成的相移φ為：ωt=ωx/c=ωx/λf=2πfx/λf=2πx/λ=βx ，這就得到了相移系數β，即一段線x所產生的相移為βx，將時間上的相移與空間上的相移相加，可得φ=ωt±βx+φ0 因此線上（一維）波的瞬時值表達式為：V=Vmsin(ωt±βx+φ0)

±號決定于波行進的方向。Φ雖然與空間有關，但它仍然是個時間變量。討論問題時，總是假定t不變（或t=0）來討論x的影響，或者x不變來討論t的影響。而在某一點上來看，即x不變，而ωt又相同，也就只與φ0有關了，這就使得兩信號之間的處理變成了平面上的矢量運算，而能測相位的網絡分析儀也就稱為矢量網絡分析儀了，

一般情況下，傳輸線上既有入射波，也有反射波，它們分別滿足相移與距離的正比關系，而一段線纜的相移卻并不一定滿足相移與長度的正比關系，除非上面沒有反射波。