摘要：

針對超寬帶室內定位系統中的測量誤差較大問題，提出了一種基于雙路飛行時間測距方法來減小時鐘偏移誤差的解決方案。本方案針對靜態和動態的待測節點的運動特性，通過對待測節點的運動狀態檢測，提出了一種聯合算法，其中，靜態定位采用了最小二乘估算法來得出節點坐標，并通過MATLAB仿真顯示該節點坐標位置；對于動態跟蹤問題，由于物體遮擋和運動軌跡等因素導致最小二乘法無法準確估計節點位置，針對這一問題，利用擴展卡爾曼濾波算法跟蹤預測待測節點位置，從而改善定位效果。仿真結果表明，靜態定位誤差可以控制在6%以內，對比靜態定位采樣，動態跟蹤算法精度提高了20%。實驗證明，該算法可靠有效，滿足室內定位的基本需求。

0 引言

隨著現代科學技術的發展，通信和導航技術已經在各個領域發揮巨大的作用，人們對位置服務的需求也越來越大［1］。在室外環境下，全球定位系統（Global Positioning System，GPS）是在室外定位采用的解決方案，定位精度一般為10 m以上［2］。在室內環境下，GPS無法解決定位問題，超寬帶（Ultra-Wide Band，UWB）技術作為室內定位技術之一，有精度高、功耗低、抗干擾能力強等特點，被廣泛應用于室內定位領域［3］。基于測距的定位方法有以下幾種：到達時間差法（Time Difference 0f Arrival，TDOA）、飛行時間法（Time Of Flight，TOF）、到達角度法（Angle Of Arrival，AOA）［4］，測量節點間的距離或角度信息，然后使用三邊測量法、三角測量法或最小二乘法計算節點位置［5］。在以往的研究中，多通過優化算法計算過程（例如Taylor算法、Fang算法、Chan算法［6］）來提高定位的精度。本文通過運動檢測的方式來區分待測節點的運動狀態，提出了一種聯合算法，采用雙路飛行時間的測距方法提高測距精度，最小二乘法（Least Square，LSE）來求解最佳節點位置，最后聯合擴展卡爾曼濾波器（Extended Kalman Filter，EFK）來跟蹤節點的運動軌跡，并通過MATLAB仿真來驗證算法的可靠性。

1 UWB測距原理

UWB系統發射的信號采用的是無載波窄脈沖，該窄脈沖的寬度一般僅為數個納秒甚至數十皮秒的數量級，這使得UWB信號具有很寬的頻譜［7］，可高達幾GHz，所以功率譜密度會很小，以上特征使得它與傳統連續無線電信號的系統不同［8］。UWB定位原理：首先測量基站與標簽之間的距離，再由算法去求解標簽的位置坐標。本文利用雙路飛行時間法（Two Way-Time Of Flight，TW-TOF）進行測距，并提出一種聯合算法求解標簽位置。

1.1 飛行時間測距法

TOF測距方法需兩節點間的協作通信，記錄UWB信號在節點間的往返時間［9］，其測距過程如圖1所示。

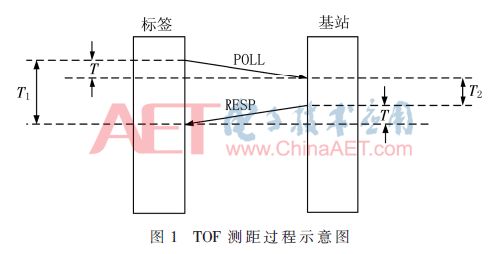
標簽向基站發送一個輪詢信息POLL，當標簽收到時，會立即回復一個確認RESP來響應這個數據包。標簽記錄從發送數據包到接收確認的時間T1；基站記錄了從收到數據包到回應的時間T2，那么基站到標簽的距離d就可以表示為：

式（1）是理想狀態下的測距公式。在TOF測距中節點用各自的時鐘計時，兩個節點的時鐘無法完全同步，導致兩節點間出現時鐘偏移，會造成比較嚴重的測距誤差。設基站的時鐘偏差為FA，標簽的時鐘偏差為FB，那么可以得到信號傳輸時間誤差：

雖然可以選用高穩定性的時鐘來減小這種誤差的影響，但價格都比較昂貴，會提高成本。

1.2 雙路飛行時間測距

對于TOF測距法中節點間的時鐘偏移而使測距誤差增大的問題，本文利用的雙路飛行時間測距法是在其基礎上進行改進的一種測距方法。其具體過程如圖2所示。

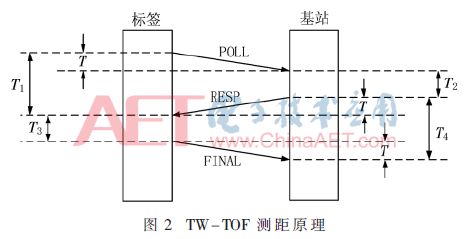
第一階段：與TOF測距法相同，得到兩個時間T1、T2。第二階段：標簽接收到RESP后，再向基站發出一個FINAL消息，設從接收到RESP到發出FINAL的時間為T3。第三階段：基站接收到FINAL后，就可以得到從發出RESP到接收到FINAL消息所用時間T4。如果按照理想TOF測距法，基站和標簽時鐘完全同步，T1=T4，T3=T2，可得：

但實際上節點之間的時鐘無法同步，所以利用TW-TOF的測距方法可以更好地控制測距帶來的誤差，從而提高定位精度。根據上述得到的幾個時間，由式（8）可以求出UWB信號的單程飛行時間T。

由此看出，TW-TOF測距大大降低了時鐘頻率偏差引起的測距誤差。如果選用低頻偏的晶體如±10×10-6Hz，可進一步降低測距理論誤差至±0.2 m。

2 最小二乘法靜態定位

2.1 最小二乘法

經過TW-TOF測距得到各個基站與標簽的距離di，同時各個基站A0、A1、A2、A3的坐標是已知的（Xi，Yi），那么就可以得到方程組：

其中：

2.2 最小二乘法靜態定位仿真

本次仿真使用的仿真軟件為MATLAB 2014b，計算機配置如下：系統環境為Windows 7 64位，CPU采用Intel CoreTMi3-3220，CPU頻率為3.30 GHz，內存為DDR3 8 GB。4個參與定位的基站坐標分別為（0，0）、（0，100）、（100，0）、（100，100），標簽的真實坐標為（44，37），最小二乘法得到的仿真結果用圓圈來表示，在測試中加入了隨機測距誤差。算法仿真運行100次以后的結果如圖3所示。

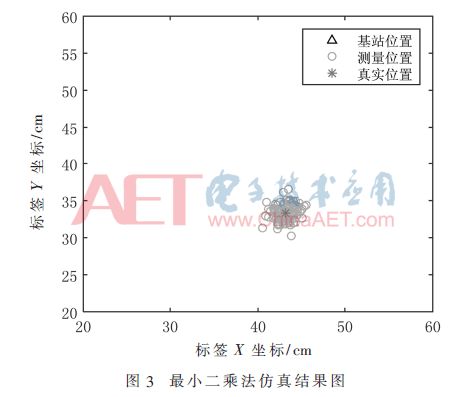
由圖3中的仿真結果可以看到，最小二乘法得到的定位結果基本上分布在標簽的真實坐標周圍，說明此定位算法有效。為了更加直觀地評價算法的表現，使用均方根誤差（Root Mean Square Error，RMSE）來分析定位誤差，如式（15）所示：

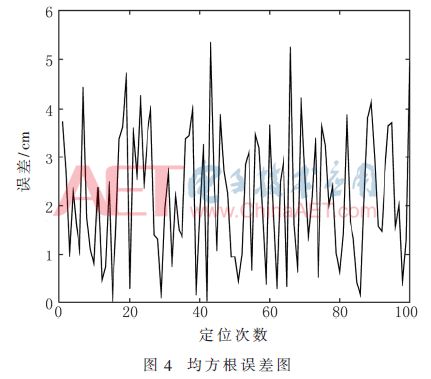
由圖4可以看出，利用最小二乘法來進行待測節點的靜態定位，定位結果誤差控制在6%以內，精確度符合預期結果，說明此算法是有效的。

3 擴展卡爾曼濾波動態定位

最小二乘法可以估測到靜態節點的位置，但是對于移動的標簽，在實際測量中由于物體或人體造成多徑傳播和非視距誤差，會導致定位誤差較大。卡爾曼濾波器利用上一時刻的位置信息和這一時刻的觀測信息對位置進行估計［10］。

3.1 擴展卡爾曼濾波器

傳統卡爾曼濾波器只能在線性高斯模型中使用，而運動標簽定位問題的模型是非線性的，那么可以使用擴展卡爾曼濾波器，用非線性函數的局部線性特征來近似非線性。其過程包括兩個階段：預測和更新［11］。

上式兩個方程分別是對k時刻狀態向量和估計誤差的協方差的預測，Q（k）是系統誤差的協方差。由于h（s（k））是非線性函數，在使用能解決非線性問題的擴展卡爾曼濾波時，使用泰勒級數展開來簡化表達式。在k-1時刻向k時刻轉換時，H（k）是h（s（k））的雅克比矩陣，即求導化簡后得：

設ω（k）和v（k）的協方差陣分別為Q（k）和R（k），都為對角矩陣，列數為2，維數是基站個數，對角線上各元素取值在仿真中分別設為定位坐標最大誤差的一半和其相應的測量方差。

3.2 動態定位仿真

為了體現擴展卡爾曼濾波在動態定位中的特性，在仿真中把它與靜態定位算法經過時間采樣后的結果進行對比，用MATLAB進行仿真，設置4個基站，分布在（0，0）、（0，1000）、（1000，0）、（1000，1000）處，本文測試的動態過程是從（0，500）處開始，來測試對動態節點的跟蹤效果。時間采樣周期為0.1 s，根據擴展卡爾曼濾波器原理，只需知道初值即可，仿真結果如圖5所示。

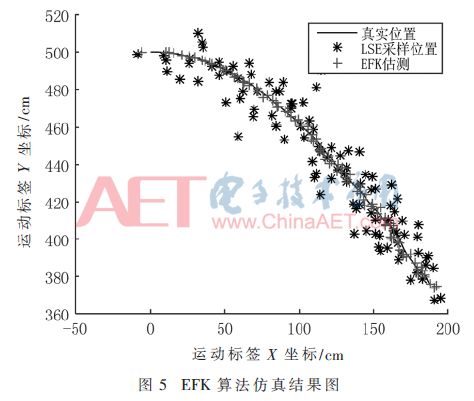
由圖5中可見，最小二乘法靜態采樣測量出的位置和經過EFK估測后形成的軌跡相比，經過EKF估測后的移動節點的坐標更接近真實的運動軌跡，說明了擴展卡爾曼濾波能更好地對運動中的標簽進行位置估計。接下來為了更直觀地顯示擴展卡爾曼濾波的動態定位效果，對比分析仿真結果的 RMSE，結果如圖6所示。

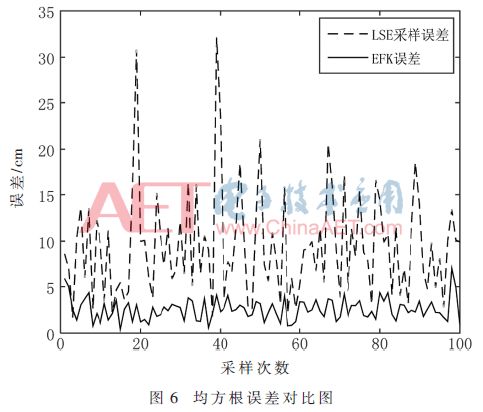
圖6中靜態算法采樣后的RMSE為波動較大的虛線，經過EFK算法估測后的RMSE為波動較小的實線，誤差從25%以內穩定到了5%左右，比較直觀地體現出了擴展卡爾曼濾波算法的有效性。

4 系統工作流程

4.1 運動狀態檢測

聯合算法的應用需要了解標簽的運動狀態，所以設計了運動狀態檢測方法。設（xt，yt）為t時刻最小二乘法靜態定位采樣所得的位置，假設系統最大誤差為σ，那么就可以通過以下的公式來檢測運動狀態：

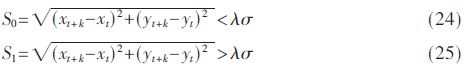
式中，k是每個測量序列的時刻，開始定位后每個測量時刻都與t時刻的位置比較。當式（24）成立時，檢測到標簽的運動狀態為靜止，相反，當式（25）成立時，也就是說在t+k時刻與t時刻的距離超過了最大誤差一定的倍數，那么就判斷標簽是運動的。經過多次仿真，最后仿真中所取的最大誤差為σ=0.2 m，誤差系數λ=2。為了防止標簽在臨界狀態下頻繁波動的情況，定義一個變量N來記錄檢測次數，只有當N》3時，也就是連續3次檢測為運動時，才能真正判定為運動狀態。用此時刻的最小二乘靜態定位的結果作為擴展卡爾曼濾波算法的初值，來繼續對標簽進行動態跟蹤定位。

4.2 聯合算法工作流程

由上文所述的聯合算法的推導和仿真，最小二乘法聯合擴展卡爾曼濾波定位算法的運算流程如圖7所示。

5 結論

本文介紹了雙路飛行時間（TW-TOF）測距法，能夠降低時鐘偏移所帶來的測距誤差，并提出了一種最小二乘靜態定位聯合擴展卡爾曼濾波動態定位算法。對于靜態定位采用了最小二乘估算法進行對待測節點定位，仿真結果表明，此算法的定位誤差能控制在6%以內；對移動的待測節點進行動態定位時，采用了擴展卡爾曼濾波器，對運動軌跡進行預測跟蹤，并通過MATLAB仿真對比表明，相對于靜態定位采樣，擴展卡爾曼濾波算法的誤差降低了20%，定位效果更好。接下來還可以通過增加基站數量和合理的基站分布位置來提高定位精度。在算法上也有優化的可能，把非線性問題轉化為線性問題的過程中，泰勒展開式中取更多的項，通過提高算法復雜度來提高精度。

參考文獻

［1］ 董家志。基于UWB的室內定位與跟蹤算法的研究［D］。成都：電子科技大學，2015.

［2］ 盧靖宇，余文濤，趙新，等。基于超寬帶的移動機器人室內定位系統設計［J］。電子技術應用，2017，43（5）：25-28.

［3］ MATTEO R，SAMUEL V D，V，HEIDI S，et al.Analysis of the scalability of UWB indoor localization solutions for high user densities［J］.Sensors，2018，18（6）：1875-1880.

［4］ 孫鳳，施偉斌，黃靈鳳。基于無線傳感器網絡的室內定位技術的研究［J］。電子技術應用，2013，39（10）：80-83.

［5］ MCELROY C，NEIRYNCK D，MCLAUGHLIN M.Comparison of wireless clock synchronization algorithms for indoor location systems［C］.Proceedings of 2014 IEEE International Conference on Communications Workshops.Sydney.IEEE，2014：157-162.

［6］ LI X，HE D，JIANG L，et al.A method indoor multi-path IR-UWB location based on multi-task compressive sensing［C］.Fourth International Conference on Ubiquitous Positioning.IEEE，2017：64-68.

［7］ HEWISH M.Ultra-wideband technology opens up new horizons［J］.Janes International Defense Review Idr，1999，2：20-22.

［8］ 梁久禎。無線定位系統［M］。北京：電子工業出版社，2013.

［9］ 魯旭陽。基于TOF的WSN節點定位技術研究［D］。鄭州：解放軍信息工程大學，2012.

［10］ 嵇茂祥.UWB室內定位系統研究與實現［D］。上海：華東師范大學，2017.

［11］ 師延山，李道本，范躍祖。無線定位擴展卡爾曼濾波算法的優化［J］。北京航空航天大學學報，2003，29（4）：308-311.