現實中常遇到多分類學習任務。有些二分類學習方法可直接推廣到多分類,如LR。但在更多情形下,我們是基于一些基本策略,利用二分類學習器來解決多分類問題。所以多分類問題的根本方法依然是二分類問題。
具體來說,有以下三種策略:
一、一對一 (OvO)
假如某個分類中有N個類別,我們將這N個類別進行兩兩配對(兩兩配對后轉化為二分類問題)。那么我們可以得到個二分類器。(簡單解釋一下,相當于在N個類別里面抽2個)
之后,在測試階段,我們把新樣本交給這個二分類器。于是我們可以得到個分類結果。把預測的最多的類別作為預測的結果。
下面,我給一個具體的例子來理解一下。
上圖的意思其實很明顯,首先把類別兩兩組合(6種組合)。組合完之后,其中一個類別作為正類,另一個作為負類(這個正負只是相對而言,目的是轉化為二分類)。然后對每個二分類器進行訓練。可以得到6個二分類器。然后把測試樣本在6個二分類器上面進行預測。從結果上可以看到,類別1被預測的最多,故測試樣本屬于類別1。
二、一對其余 (OvR)
一對其余其實更加好理解,每次將一個類別作為正類,其余類別作為負類。此時共有(N個分類器)。在測試的時候若僅有一個分類器預測為正類,則對應的類別標記為最終的分類結果。例如下面這個例子。
大概解釋一下,就是有當有4個類別的時候,每次把其中一個類別作為正類別,其余作為負類別,共有4種組合,對于這4種組合進行分類器的訓練,我們可以得到4個分類器。對于測試樣本,放進4個分類器進行預測,僅有一個分類器預測為正類,于是取這個分類器的結果作為預測結果,分類器2預測的結果是類別2,于是這個樣本便屬于類別2。
其實,有人會有疑問,那么預測為負類的分類器就不用管了嗎?是的,因為預測為負類的時候有多種可能,無法確定,只有預測為正類的時候才能唯一確定屬于哪一類。比如對于分類器3,分類結果是負類,但是負類有類別1,類別2,類別4三種,到底屬于哪一種?
OvO和OvR有何優缺點?
容易看出,OvR只需訓練N個分類器,而OvO需訓練N(N - 1)/2個分類器, 因此,OvO的存儲開銷和測試時間開銷通常比OvR更大。但在訓練時,OvR的每個分類器均使用全部訓練樣例,而OvO的每個分類器僅用到兩個類的樣例,因此,在類別很多時,OvO的訓練時間開銷通常比OvR更小。至于預測性能,則取決于具體的數據分布,在多數情形下兩者差不多。
綜上:
OvO的優點是,在類別很多時,訓練時間要比OvR少。缺點是,分類器個數多。
OvR的優點是,分類器個數少,存儲開銷和測試時間比OvO少。缺點是,類別很多時,訓練時間長。
三、多對多(MvM)
MvM是每次將若干個類作為正類,若干個其他類作為反類。顯然,OvO和OvR是MvM的特例。MvM的正、反類構造必須有特殊的設計,不能隨意選取。這里我們介紹一種最常用的MvM技術"糾錯輸出碼" (Error Correcting Output Codes,簡稱 ECOC)
ECOC是將編碼的思想引入類別拆分,并盡可能在解碼過程中具有容錯性。
ECOC工作過程主要分為兩步:
編碼:對N個類別做M次劃分,每次劃分將一部分類別劃為正類,一部分劃為反類,從而形成一個二分類訓練集。這樣一共產生M個訓練集,可訓練出M個分類器。
解碼:M 個分類器分別對測試樣本進行預測,這些預測標記組成一個編碼。將這個預測編碼與每個類別各自的編碼進行比較,返回其中距離最小的類別作為最終預測結果。
類別劃分通過"編碼矩陣"指定。編碼矩陣有多種形式,常見的主要有二元碼和三元碼。前者將每個類別分別指定為正類和反類,后者在正、反類之外,還可指定"停用類"。圖3.5給出了一個示意圖,在圖 3.5(a) 中,分類器f2將Cl類和C3類的樣例作為正例,C2類和C4類的樣例作為反例;在圖3.5(b)中,分類器f4將C1類和C4類的樣例作為正例,C3 類的樣例作為反例。在解碼階段,各分類器的預測結果聯合起來形成了測試示例的編碼,該編碼與各類所對應的編碼進行比較,將距離最小的編碼所對應的類別作為預測結果。
例如在圖 3.5(a) 中,若基于歐式距離,預測結果將是 C3。也就是一個測試樣本,經過分類器f1,f2,f3,f4,f5分別預測成了(-1,-1,+1,-1,+1),與C1相比較,海明距離為0+1+1+1+0=3,歐式距離為,對C2,C3,C4都進行比較即可。
為什么稱為"糾錯輸出碼"呢?
這是因為在測試階段,ECOC編碼對分類器的錯誤有一定的容忍和修正能力。例如圖3.5(a) 中對測試示例的正確預測編碼是(-1,+1,+1,-1,+1),假設在預測時某個分類器出錯了,例如 h 出錯從而導致了錯誤編碼(-1,-1,+1,-1,+1),但基于這個編碼仍能產生正確的最終分類結果C3。一般來說,對同一個學習任務,ECOC編碼越長,糾錯能力越強。
EOCO編碼長度越長,糾錯能力越強,那長度越長越好嗎?
NO!編碼越長,意味著所需訓練的分類器越多,計算、存儲開銷都會增大;另一方面,對有限類別數,可能的組合數目是有限的,碼長超過一定范圍后就失去了意義。
對同等長度的編碼,理論上來說,任意兩個類別之間的編碼距離越遠,則糾錯能力越強。因此,在碼長較小時可根據這個原則計算出理論最優編碼。然而,碼長稍大一些就難以有效地確定最優編碼,事實上這是 NP 難問題。不過,通常我們并不需獲得理論最優編碼,因為非最優編碼在實踐中往往己能產生足夠好的分類器。另一方面,并不是編碼的理論性質越好,分類性能就越好,因為機器學習問題涉及很多因素,例如將多個類拆解為兩個“類別子集”,不同拆解方式所形成的兩個類別子集的區分難度往往不同,即其導致的二分類問題的難度不同。于是一個理論糾錯性質很好、但導致的二分類問題較難的編碼,與另一個理論糾錯性質差一些、但導致的二分類問題較簡單的編碼,最終產生的模型性能孰強孰弱很難說。
-
分類器
+關注
關注
0文章
152瀏覽量
13196 -
機器學習
+關注
關注
66文章
8422瀏覽量
132723
原文標題:機器學習中的多分類任務詳解
文章出處:【微信號:Imgtec,微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Keras之ML~P:基于Keras中建立的簡單的二分類問題的神經網絡模型
基于Keras中建立的簡單的二分類問題的神經網絡模型(根據200個數據樣本預測新的5+1個樣本)—類別預測
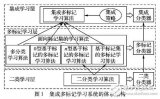
集成學習的多分類器動態組合方法
基于主動學習不平衡多分類AdaBoost改進算法
多分類孿生支持向量機研究進展
基于可能性二均值聚類的二分類支持向量機
解決二分類問題的算法——AdaBoost算法

如何使用數字語音取證算法設計一個多分類器的詳細資料說明
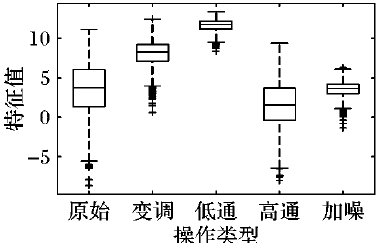




 如何利用二分類學習器來解決多分類問題
如何利用二分類學習器來解決多分類問題
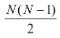










評論