根據受歡迎程度,線性回歸和邏輯回歸經常是我們做預測模型時,且第一個學習的算法。但是如果認為回歸就兩個算法,就大錯特錯了。事實上我們有許多類型的回歸方法可以去建模。每一個算法都有其重要性和特殊性。
內容
1.什么是回歸分析?
2.我們為什么要使用回歸分析?
3.回歸有哪些類型 ?
4.線性回歸
5.邏輯回歸
6.多項式回歸
7.逐步回歸
8.嶺回歸
9.Lasso回歸
10.ElasticNet回歸
什么是回歸分析?
回歸分析是研究自變量和因變量之間關系的一種預測模型技術。這些技術應用于預測,時間序列模型和找到變量之間關系。例如可以通過回歸去研究超速與交通事故發生次數的關系。
我們為什么要用回歸分析?
這里有一些使用回歸分析的好處:它指示出自變量與因變量之間的顯著關系;它指示出多個自變量對因變量的影響。回歸分析允許我們比較不同尺度的變量,例如:價格改變的影響和宣傳活動的次數。這些好處可以幫助市場研究者/數據分析師去除和評價用于建立預測模型里面的變量。
回歸有哪些類型?
我們有很多種回歸方法用預測。這些技術可通過三種方法分類:自變量的個數、因變量的類型和回歸線的形狀。
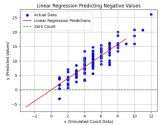
1.線性回歸
線性回歸可謂是世界上最知名的建模方法之一,也是應該是我們第一個接觸的模型。在模型中,因變量是連續型的,自變量可以使連續型或離散型的,回歸線是線性的。
線性回歸用最適直線(回歸線)去建立因變量Y和一個或多個自變量X之間的關系。可以用公式來表示:
Y=a+b*X+e
a為截距,b為回歸線的斜率,e是誤差項。
簡單線性回歸與多元線性回歸的差別在于:多元線性回歸有多個(》1)自變量,而簡單線性回歸只有一個自變量。到現在我們的問題就是:如何找到那條回歸線?
我們可以通過最小二乘法把這個問題解決。其實最小二乘法就是線性回歸模型的損失函數,只要把損失函數做到最小時得出的參數,才是我們最需要的參數。
我們一般用決定系數(R方)去評價模型的表現。
重點:
1.自變量與因變量之間必須要有線性關系。
2.多重共線性、自相關和異方差對多元線性回歸的影響很大。
3.線性回歸對異常值非常敏感,其能嚴重影響回歸線,最終影響預測值。
4.在多元的自變量中,我們可以通過前進法,后退法和逐步法去選擇最顯著的自變量。
2. 邏輯回歸
邏輯回歸是用來找到事件成功或事件失敗的概率。當我們的因變量是二分類(0/1,True/False,Yes/No)時我們應該使用邏輯回歸。
重點:
1.在分類問題中使用的非常多。
2.邏輯回歸因其應用非線性log轉換方法,使得其不需要自變量與因變量之間有線性關系。
3.為防止過擬合和低擬合,我們應該確保每個變量是顯著的。應該使用逐步回歸方法去估計邏輯回歸。
4.邏輯回歸需要大樣本量,因為最大似然估計在低樣本量的情況下表現不好。
5.要求沒有共線性。
6.如果因變量是序數型的,則稱為序數型邏輯回歸。
7.如果因變量有多個,則稱為多項邏輯回歸。
3. 多項式回歸
如果一個回歸,它的自變量指數超過1,則稱為多項式回歸。可以用公式表示:
y = a + b * x^2
在這個回歸技術中,最適的線不是一條直線,而是一條曲線。
重點:
① 很多情況下,我們為了降低誤差,經常會抵制不了使用多項式回歸的誘惑,但事實是,我們經常會造成過擬合。所以要經常的把數據可視化,觀察數據與模型的擬合程度。
② 特別是要看曲線的結尾部分,看它的形狀和趨勢是否有意義。高的多項式往往會產生特別古怪的預測值。
4. 逐步回歸
當我們要處理多個自變量時,我們就需要這個回歸方法。在這個方法中選擇變量都是通過自動過程實現的,不需要人的干預。
這個工程是通過觀察統計值,比如判定系數,t值和最小信息準則等去篩選變量。逐步回歸變量一般是基于特定的標準加入或移除變量來擬合回歸模型。
一些常用的逐步回歸方法如下:
1. 標準逐步回歸做兩件事情。只要是需要每一步它都會添加或移除一些變量。
2. 前進法是開始于最顯著的變量然后在模型中逐漸增加次顯著變量。
3. 后退法是開始于所有變量,然后逐漸移除一些不顯著變量。
4. 這個模型技術的目的是為了用最少的變量去最大化模型的預測能力。它也是一種降維技術。
5. 嶺回歸
當碰到數據有多重共線性時,我們就會用到嶺回歸。所謂多重共線性,簡單的說就是自變量之間有高度相關關系。在多重共線性中,即使是最小二乘法是無偏的,它們的方差也會很大。通過在回歸中加入一些偏差,嶺回歸酒會減少標準誤差。
‘嶺回歸是一種專用于共線性數據分析的有偏估計回歸方法,實質上是一種改良的最小二乘估計法,通過放棄最小二乘法的無偏性,以損失部分信息、降低精度為代價獲得回歸系數更為符合實際、更可靠的回歸方法,對病態數據的擬合要強于最小二乘法。’ ---百度百科
嶺回歸是通過嶺參數λ去解決多重共線性的問題。看下面的公式:
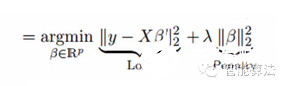
其中loss為損失函數,penalty為懲罰項。
重點:
1.嶺回歸的假設與最小二乘法回歸的假設相同除了假設正態性。
2.它把系數的值收縮了,但是不會為0.
3.正則化方法是使用了l2正則。
6. LASSO回歸
和嶺回歸類似,Lasso(least Absolute Shrinkage and Selection Operator)也是通過懲罰其回歸系數的絕對值。看下面的公式:
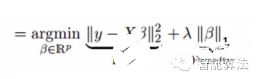
Lasso回歸和嶺回歸不同的是,Lasso回歸在懲罰方程中用的是絕對值,而不是平方。這就使得懲罰后的值可能會變成0.
重點:
1.其假設與最小二乘回歸相同除了正態性。
2.其能把系數收縮到0,使得其能幫助特征選擇。
3.這個正則化方法為l1正則化。
4.如果一組變量是高度相關的,lasso會選擇其中的一個,然后把其他都變為0.
7. ElasticNet回歸
ElasticNet回歸是Lasso回歸和嶺回歸的組合。它會事先訓練L1和L2作為懲罰項。當許多變量是相關的時候,Elastic-net是有用的。Lasso一般會隨機選擇其中一個,而Elastic-net則會選在兩個。
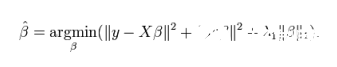
與Lasso和嶺回歸的利弊比較,一個實用的優點就是Elastic-Net會繼承一些嶺回歸的穩定性。
重點:
1.在選擇變量的數量上沒有限制
2.雙重收縮對其有影響
3.除了這7個常用的回歸技術,你也可以看看貝葉斯回歸、生態學回歸和魯棒回歸。
如何選擇回歸模型?
面對如此多的回歸模型,最重要的是根據自變量因變量的類型、數據的維數和其他數據的重要特征去選擇最合適的方法。以下是我們選擇正確回歸模型時要主要考慮的因素:
1.數據探索是建立預測模型不可或缺的部分。它應該是在選擇正確模型之前要做的。
2.為了比較不同模型的擬合程度,我們可以分析不同的度量,比如統計顯著性參數、R方、調整R方、最小信息標準、BIC和誤差準則。另一個是Mallow‘s Cp準則。
3.交叉驗證是驗證預測模型最好的方法。你把你的數據集分成兩組:一組用于訓練,一組用于驗證。
4.如果你的數據集有許多讓你困惑的變量,你就不應該用自動模型選擇方法,因為你不想把這些變量放在模型當中。
5.不強大的模型往往容易建立,而強大的模型很難建立。
6.回歸正則方法在高維度和多重共線性的情況下表現的很好。
-
機器學習
+關注
關注
66文章
8428瀏覽量
132845
發布評論請先 登錄
相關推薦
基于移動自回歸的時序擴散預測模型
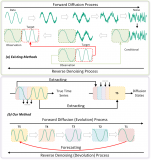




 機器學習的回歸分析和回歸方法
機器學習的回歸分析和回歸方法












評論