頻率響應是指以正弦波作為命令輸入來繪制機器或過程輸出的動態響應。測試設備可用于測試物理系統，并且存在允許使用完全理論方法的分析技術和工具。在這里，我們將簡要介紹一下作為測試過程的頻率響應方法，并總結系統設計師可以從這些過程和結果中獲得什么。

如果可以用正弦測試信號激勵設備并測量其輸出，則頻率響應測試方法可以應用于任何事物。在電液運動控制中，制造商為伺服和比例閥發布的數據中最常遇到頻率響應。實際上，我之所以主張使用伺服閥和比例閥（而不是其他類型的閥）的一個令人信服的原因是，因為伺服閥和比例閥存在太多的頻率響應數據，而其他設備幾乎沒有。有了這些信息，我們就可以在構建系統之前更好地預測系統的性能。

頻率響應測試非常簡單，觀察幾分鐘后即可輕松理解。這與在純學術環境中學習數月相反。這是一種用于測量元件（例如閥）動態響應的方法。

另一種流行的動態測試程序是測量對階躍輸入的輸出響應。頻率響應和階躍響應是相關的，因為它們來自同一系統。但是，頻率響應方法比階躍響應更可靠，因為在使用頻率響應分析儀時，在頻率響應測試中固有地抑制了失真和噪聲。

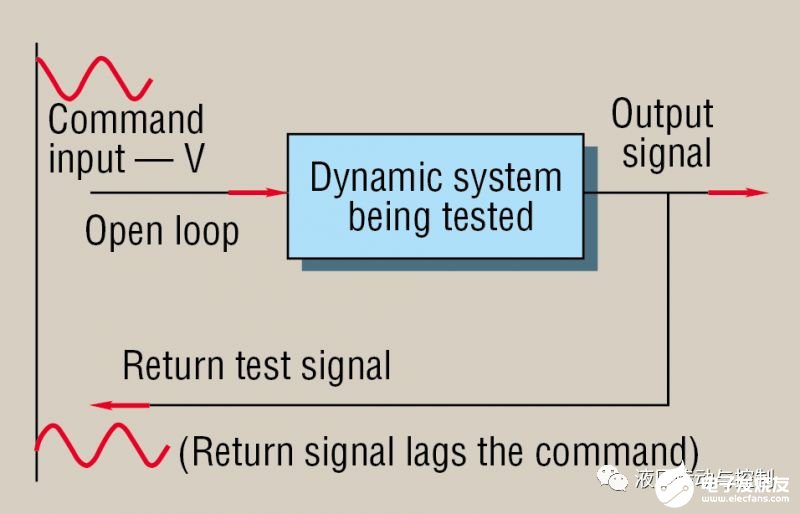
圖1.圖顯示了頻率響應測試環路的框圖。頻率響應可用作動態測試，因為當與頻率響應分析儀結合使用時，它固有地抑制了失真和噪聲。

如圖1所示，該測試涉及對輸入施加受控幅度的正弦波形，從而使被測設備（例如閥）來回循環。同時，輸出也將以相同的頻率循環。但是，輸出和指令輸入的幅值不一定與指令輸入相同。就閥門而言，輸入（電流）和輸出（流量）甚至不在相同的度量單位中。此外，在大多數實際物理動態過程中，輸出將經歷相位滯后。即，輸出必須一定落后于輸入。測試操作員記錄頻率，輸出幅值以及輸入和輸出之間的相位滯后量（以度為單位）。

接下來，增加頻率，同時將輸入正弦波保持在恒定的峰-峰值幅值。通常以度為單位繪制相位，并通過以下等式以分貝（dB）給出幅值：

A = 20 log | On÷Ol |

其中

A：閥頻率響應的幅值

On：是任意頻率的輸出，并且

Ol：是最低頻率的輸出。因此，我們看到，對于最低的測試頻率，伺服閥的頻率響應測試數據始終從0 dB開始。

在較高的測試頻率下，通常會出現較高的相位滯后，并且輸出幅值會發生變化。在任何類型的機器上，隨著頻率的增加，輸出幅值將無法跟上輸入幅值，這是正常現象。也就是說，總會有一些頻率的輸入命令振動得如此之快，以至于輸出根本無法跟上。因此，輸出幅值趨于隨頻率增加而減小，并且輸入與輸出之間的相位滯后趨于增大。

也有例外。當被測系統中存在共振時，在某些狹窄的頻帶或范圍內，輸出幅值會隨頻率增加。當存儲在彈簧或其他撓性構件中的勢能與運動質量的動能交換時，就會發生共振。當質量的動能與內部壓縮流體中存儲的勢能相互作用時，會在液壓系統中產生共振。

當發生共振時，有時會隨著輸出振幅的增加而顯示出共振，從而增加頻率。圖2中所示的伺服閥頻率響應數據就是這種情況。在30 Hz時，比0 dB參考值高出約0.8 dB。共振上升的存在表明閥有彈性的趨勢，如果使用階躍輸入進行測試，則閥的輸出將趨向于在該頻率附近“響”。上升表明閥的設計者將其響應調整為阻尼不足。大多數伺服閥已調整為無共振上升。但是，也有一些例外。阻尼不足的特性伴隨著共振上升。描述這種情況的一種方法是，“欠阻尼意味著存在過沖和共振上升”。

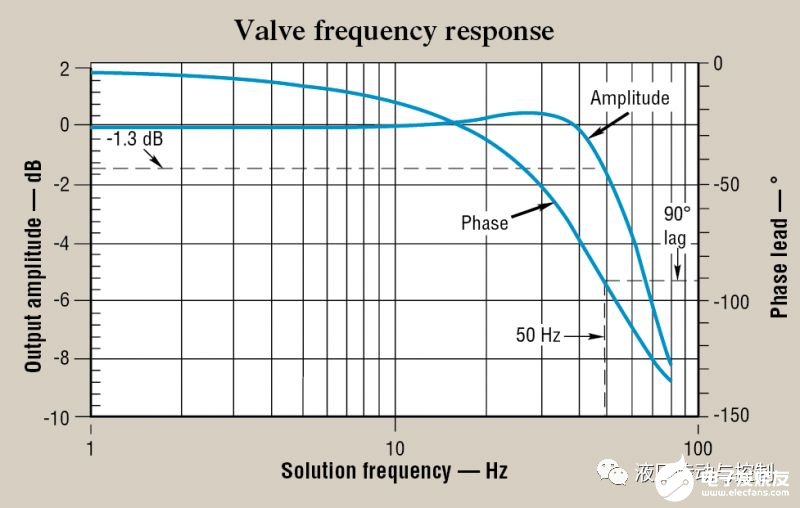
圖2.伺服閥頻率響應數據顯示了當質量的動能與壓縮流體中存儲的勢能相互作用時，液壓系統中如何發生共振。振幅在30 Hz左右的升高表明存在共振，并且該閥設計為具有稍微欠阻尼的響應。

圖2中的頻率響應圖至少是許多伺服閥的典型特性，可以用來比較一個閥與另一個閥的響應。任何閥的重要“基準”頻率是相位滯后達到90°的頻率。請注意，在參考閥中，頻率約為50 Hz。顯然，如果有另一個閥門的90°相位滯后頻率高于50 Hz，則該閥門的響應速度將比圖2中所示的更快。

將一個閥與另一個閥進行比較時，應始終使用90°相位滯后頻率。該頻率稱為閥頻率，閥頻率響應或閥帶寬。所有術語或多或少都是同義詞。無論如何，該頻率有助于預測閥響應與應用系統所需性能之間的匹配程度。一些設計人員使用-3dB的頻率。但是，作為比較基準，這是不可靠的。在評估閥門與最終系統中其余部件的配合情況時，它也沒有價值。90°相位滯后頻率的最重要特征是，它使我們能夠將閥頻率與液壓機械共振頻率進行比較，液壓共振頻率是由于流體的可壓縮性（液壓電容或柔量）與執行器負載質量相互作用而產生的共振。

一些背景

在奈奎斯特（Nyquist）的開創性論文中，他將正弦分析的思想應用到了動態系統中，但是在當時非常受其它影響的情況下，他以非常神秘的數學術語將其應用。九年后，Bode發表了同樣重要的論文。他教我們，通過以分貝表示正弦頻率響應的幅值，將一個設備（例如閥）的幅值和相位響應與另一設備（例如負載和執行器子系統）的幅值和相位響應相加就變得很簡單。在那時，當選擇計算輔助成為計算規則時，確實如此受歡迎。盡管計算機發生了革命性的變化，并且計算機執行復雜的計算非常容易，但是眾所周知的Bode圖仍然是系統設計人員最喜歡的工具。

Bode和Nyquist（都是貝爾實驗室的研究工程師）對確定為什么某些音頻放大器會突然振蕩而另一些音頻放大器不會突然振蕩的想法很感興趣。如今，運動控制和反饋控制系統的設計人員仍在為機器的振動問題而苦苦掙扎。如果繼續下去，這種振蕩可能是自毀的。頻率響應方法使我們能夠合理估計將產生穩定的，無振蕩的伺服機構的電子調諧極限。

博德的方法要求我們測試和研究開環系統，然后使用分析技術詢問“假如是”閉環會如何。例如，可以在開環配置中測試完整的位置伺服機構（圖3），以找到使系統不穩定的必要條件。請注意，我們不是使用正弦測試數據（頻率響應特性）來確定系統在正弦輸入下的性能，而是在系統振蕩之前可以獲得多少伺服環路增益。這就是頻率響應方法的精妙之處。

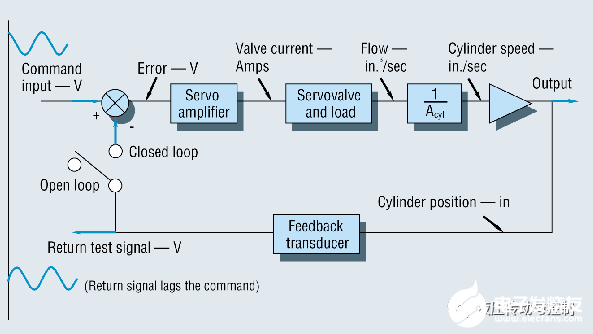
圖3.左側的開關允許在開環配置下測試該閉環電液系統，以確定引起不穩定的頻率響應特性。然后，該系統可以以減少到引起振蕩的增益的一半左右的增益進行操作。

為了說明這一點，請考慮圖3的系統。它將首先在開環位置使用反饋開關進行測試。隨著頻率的增加，我們尋找在指令輸入和開環反饋信號之間造成180°相位滯后的任何頻率。（在水力機械系統中，基本上可以確定存在此頻率。）在該頻率下，如果輸出（開環反饋信號）的幅值等于或大于輸入命令幅值，則可以閉合反饋開關。然后，通過負反饋過程，該180°相位移將經另一個180°相位。結果是可以消除正弦指令輸入激勵，并且閉環系統將處于持續振蕩狀態。這是一個不穩定的系統，如果無法停止振蕩，則是不切實際的。減小伺服環路增益是停止振蕩的正常過程。這是通過更改伺服放大器的增益設置來實現的。

上一段以非數學的形式提出了伺服回路穩定性的經典標準。通過更改對180°相位頻率的搜索，可以簡化一點。考慮以下情況：假設在搜索中找到了臨界的180°相位頻率，但是開環反饋信號的幅值小于命令輸入幅值。該頻率下的開環增益小于1，在分貝標度上小于零。

現在我們問自己：“如何增加增益，使反饋信號幅值等于指令信號幅值（伺服環路增益為零dB）？”我們只需要增加伺服放大器的增益，系統就會陷入振蕩。因此，只要有180°的相位頻率，只要增加伺服放大器的增益即可實現持續振蕩。每個電液系統都存在一個180°的相位頻率，因此我們始終可以將這種系統調整到不穩定的程度。

當然，我們不希望系統振蕩。調整到不穩定點的目的是找到將產生不穩定的最終增益。然后將增益減小到引起穩定振蕩的值的一半左右，并留在那里。增益降低50％大約等于5 dB的增益裕度。即，將增益設置為低于不穩定點5 dB。對于許多電動液壓運動控制系統而言，這已足夠。在設計過程中使用頻率響應方法，我們可以預測不穩定性的增益。因此，我們可以從不穩定性中估計出伺服系統中預期的誤差。

共振頻率和閥頻率

流體力學共振頻率（HMRF）與流體體積和負載質量成反比：受壓流體體積越大，負載質量越大，HMRF越低。HMRF越低，實現伺服系統的快速響應控制就越困難。相反，系統變得緩慢而富有彈性。確實，有些人將流體的可壓縮性等同于彈簧。這個比喻有一定的價值。

當HMRF太低時，這種彈性可能是系統的瓶頸。我見過HMRF低至0.5 Hz，高至700Hz以及介于兩者之間的所有值的系統。HMRF低是大負載質量連接到小油缸的特征。增加油缸面積始終具有提高HMRF的作用。當HMRF小于閥的頻率時，它將成為系統的瓶頸。閥頻率fv是根據閥門制造商發布的頻率響應測試數據產生90°相位滯后的頻率。

現在，我們有了將一種頻率與另一種頻率進行比較的直接基礎，這使我們能夠得出重要的結論。的確，當小于閥頻率時，HMRF會限制系統響應。但是，當閥的頻率小于HMRF時，閥將成為限制裝置。規則很簡單：動態瓶頸是fv和fn中的較小者。

通常，當系統的HMRF小于其閥頻率時，很難設計出具有清晰響應的系統。不幸的是，系統的HMRF通常低于其閥頻率。因此，這意味著HMRF通常是主要的，這代表了最具挑戰性的設計方案。換句話說，最壞的情況是最常見的情況。

此外，當閥頻率約為HMRF的兩倍時，提高閥頻率對系統性能的影響可忽略不計，因為性能將幾乎完全受到HMRF的影響。應該清楚的是，閉環帶寬必須始終小于fv和fn中的較小者。唯一剩下的問題是：少多少？

閉環帶寬的限制

最大閉環帶寬（頻率響應）必須小于一個稱為分離比的值，該值始終小于1。用數學術語來說：

fmax 《 ps ×（lesser of fv or fn）（fv 或fn中的較小者），

其中

fmax 是最大系統關閉帶寬

ps 是分離率，并且

fv 和 fn是閥和油缸負載共振頻率，單位為Hz。

當HMRF占主導地位（《fv）時，分離比完全由液壓機械系統的阻尼比控制：

ps =2Zn

其中

Zn是阻尼比，是振動減弱趨勢的度量。

造成阻尼的因素有兩個：從執行器一側到另一側的內部泄漏（無論是從執行器內部還是從控制閥內部泄漏）和摩擦（是否來自執行器或其負載）。由于制造商努力減少內部泄漏和摩擦，因此大多數液壓機械系統的阻尼度可能會非常低，這不足為奇。實際上，當負載可以以可忽略的摩擦力移動時（如由循環線性球軸承支撐時），阻尼比可能低至0.03或0.05。誠然，系統摩擦和阻尼比是要在系統中評估的最難以捉摸的量。但是，它們與頻率一起絕對控制著系統的性能極限。

計算示例

考慮一個示例來演示此討論。假設已計算出系統的油缸機械共振頻率，發現其為18 Hz。進一步假設其伺服閥的90°相位滯后頻率為65 Hz，并且由于摩擦和內部閥門泄漏，我們估計液壓機械阻尼比約為0.05。我們可以計算出最大可能的閉環系統帶寬：

fmax 《 ps x（ fv 或 fn的小者）

fmax 《2 x 0.05 x 18

fmax 《1.8 Hz

最大閉環帶寬fmax 只有1.8 Hz，僅為HMRF的十分之一！在啟動時，我們通過增加伺服放大器增益來增加系統帶寬。如果我們增加增益直到帶寬達到1.8 Hz，然后再嘗試進一步增加，則伺服回路將陷入持續的振蕩狀態，從而變得毫無價值。必須降低增益以重新建立穩定性。

系統帶寬之所以重要，是因為它與定位精度（或更準確地說，是定位誤差和跟隨誤差）之間存在直接的反比關系。已經表明：

?xp = （?IT × Gsp）/（2’ fsys）

其中

?xp 是預期的穩態定位誤差（in。）

?IT 是由八種已知的外部干擾引起的總預期閥電流變化（安培），

Gsp是最高預期速度和負載下的速度增益［（in.x A）/秒］，并且

fsys是實際的閉環系統帶寬（Hz）。

輸出位置永遠不會是我們想要的位置-只能關閉。電液位置伺服機構中存在八種導致定位不完善的已知干擾：

? 閥溫度變化

? 供油壓力變化

? 回油箱油口壓力變化

? 分離摩擦

? 負載變化

? 閥滯環

? 閥閾值，以及

? 閥死區。

所有這些必須分解為等效的閥電流，然后加在一起得出總的預期閥電流，即IT增量。總的來說，評估給定系統的這八個“錯誤貢獻者”不僅僅是一個瑣碎的過程。但是，經驗告訴我們，對于具有“典型”伺服閥性能的零遮蓋閥，?IT 約為閥額定電流的2％或3％。如果閥是成比例的并且具有實質性的遮蓋，則我們通常僅使用遮蓋而忽略其他七個貢獻者。

從技術上講，對于最壞的負載條件，必須使用所選控制閥的特性來計算速度增益。如果設計人員采用良好的工程實踐來選擇控制閥（如果選擇該閥以在最壞的負載和速度組合下提供最大的功率傳遞），那么速度增益Gsp將等于目標設計執行器速度除以約為閥額定電流的2/3。有了這些信息，我們現在可以估計預期的系統“準確性”。

假設我們正在設計的系統在最壞情況下必須使用基本上為零遮蓋的伺服閥以21in./sec的速度推動負載。可以首先計算該頁面左上部分的分子：

?IT × Gsp = （0.02 × IR x 21） ÷ （0.67× IR），

其中

IR是閥的額定電流，可以從公式中抵消。

現在

?IT Gsp=（0.02×21）×0.67

?IT Gsp = 0.63英寸/秒

如果我們假設伺服回路已經在不穩定性發生之前調整到允許的最大值，則fsys設置為fmax，因此可以估算誤差：

?xp = ?IT Gsp÷2 ’ fsys

但是由于分子已經被求值：

?xp = 0.63÷（2′×1.8），

?xp=±0.055 in

這樣，我們可以預期該系統的長期定位能力約為0.055 in。

責任編輯：gt