(文章來源:博科園)
拓撲材料引起了科學家們的極大興趣,并可能為材料發展的新紀元提供基礎。在發表在《科學進展》期刊上的研究,安德烈亞斯·艾爾本、余金龍、彼得·佐勒和伯努瓦·弗默施等物理學家提出了一種新的測量方法,可以識別和表征各種實驗平臺上的所謂拓撲不變量。今天,現代量子模擬器為制備和研究復雜量子態提供了廣泛的可能性:
它們是用光學晶格中的超冷原子、里德堡態原子、囚禁離子或超導量子比特實現的。一類特別吸引人的量子態是物質的拓撲態。大衛·索利斯(David Thouless)、鄧肯·霍爾丹(Duncan Haldane)和邁克爾·科斯特利茨(Michael Kosterlitz)因其理論發現而獲得2016年諾貝爾物理學獎。這些物質的狀態以非局域量子關聯為特征,對實驗中不可避免地發生的局域扭曲特別穩定。
因斯布魯克大學量子物理中心和奧地利科學院量子光學和量子信息研究所的伯努瓦·韋默施、于金龍和安德烈亞斯·埃爾本說:在實驗中識別和表征這些拓撲相是一個巨大挑戰。由于拓撲相的特殊性質,無法通過局部測量來識別它們。因此,研究正在開發新的測量協議,使實驗物理學家能夠在實驗室中表征這些狀態。近年來,非交互系統已經實現了這一點。然而,對于未來也可能被用作拓撲量子計算機的交互系統來說,這到目前為止還不可能。
彼得·佐勒研究小組的物理學家現在提出了測量協議,使所謂的拓撲不變量測量成為可能。這些數學表達式描述了拓撲空間的共同性質,使得在一維玻色系統中完全識別具有全局對稱性的相互作用拓撲態成為可能。研究的想法是首先在量子模擬器中準備這樣的拓撲態,現在進行所謂的隨機測量,并從這些隨機測量的統計相關性中提取拓撲不變量。
該方法的特點是:雖然拓撲不變量是高度復雜的非局部相關函數,但它們仍然可以從簡單局部隨機測量的統計相關性中提取出來。就像研究小組提出在計算機或模擬器中比較量子態的方法一樣,這種隨機測量在今天的實驗中是可能的。因此,測量拓撲不變量的協議,可以直接應用于現有的實驗平臺。多體拓撲不變量作為多體波函數的量子化高度非局域相關器,是多體拓撲量子相理論描述的核心,包括對稱性保護和對稱性豐富的拓撲相。
在這里,研究提出并分析了一個通用的測量協議,以揭示具有全局對稱性的相位多體拓撲不變量,可以在合成量子系統(如里德堡原子、囚禁離子和超導電路)的最新實驗中實現。該協議基于從隨機化測量的統計相關性中提取多體拓撲不變量,通過局部隨機么正運算和站點分辨投影測量來實現。并在一維玻色對稱保護拓撲相的完全分類背景下,特別考慮到擴展的SU-Schrieffer-Heeger自旋模型,說明了這一技術及其應用。
(責任編輯:fqj)
-
量子信息
+關注
關注
0文章
53瀏覽量
12754 -
量子比特
+關注
關注
0文章
38瀏覽量
8837
發布評論請先 登錄
相關推薦
量子隱形傳態通過普通光纜成功傳輸
上海光機所提出強激光產生高能量子渦旋態電子新方法

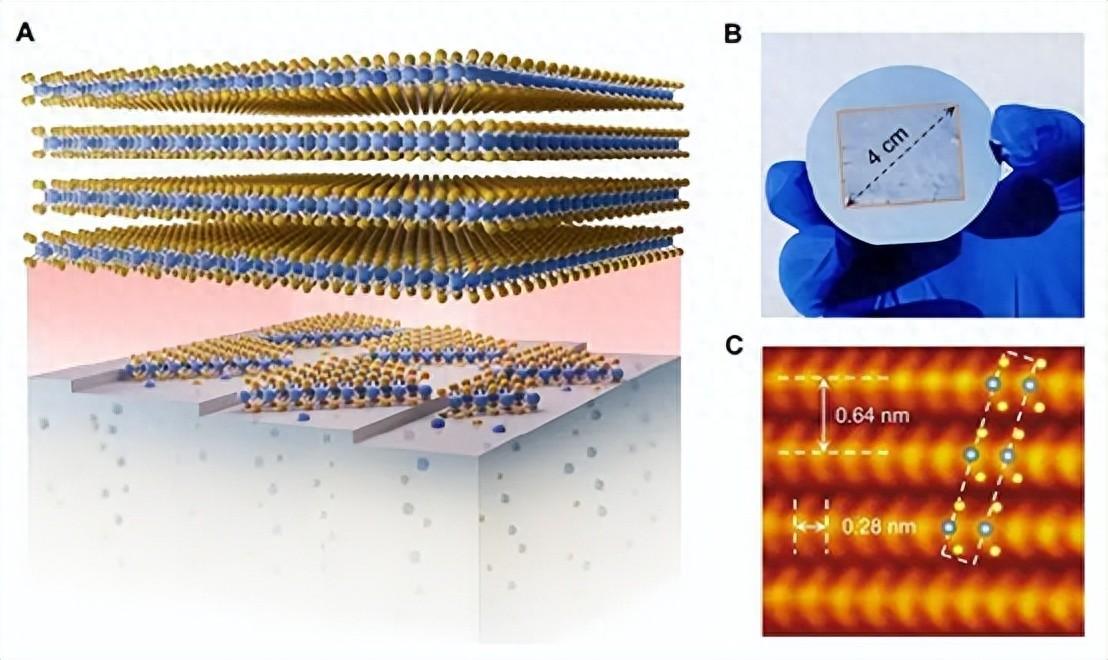
從“蓋房子”到“頂竹筍”:我國科學家首創晶體制備新方法
本源量子參與的國家重點研發計劃青年科學家項目啟動會順利召開

量子互聯網關鍵連接首次實現
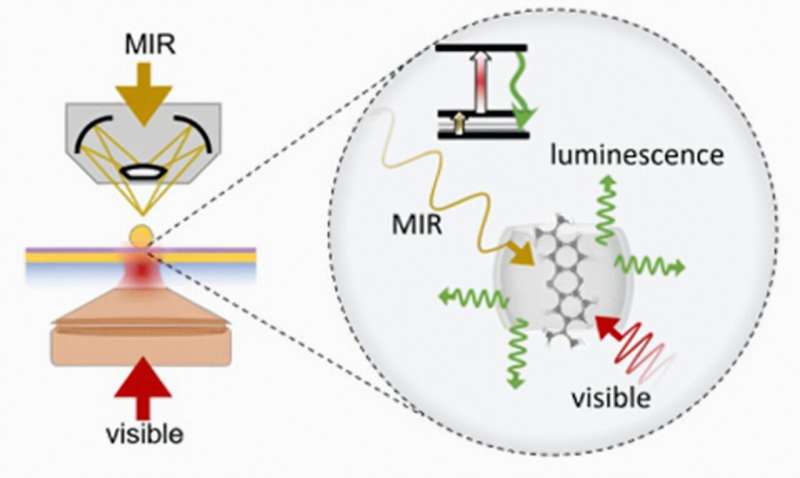
使隱形可見:新方法可在室溫下探測中紅外光
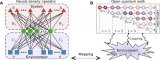
光量子行走的高效機器學習技術研究




 科學家發明新方法,可識別各種拓撲不變量的量子態
科學家發明新方法,可識別各種拓撲不變量的量子態











評論