動機:為了更好的理解深度學習,作者決定從零開始建立一個神經網絡,而不是像TensorFlow這樣的深度學習庫。相信理解神經網絡的內部工作對于任何有抱負的數據科學家來說都是很重要的。
什么是神經網絡?
大多數介紹神經網絡的文章在描述它們時會涉及到大腦類比,在不深入研究大腦類比的情況下,將神經網絡簡單描述為將固定數值映射到期望輸出的數學函數理解起來更容易。
神經網絡由以下部分組成:
輸入層,x
任意數量的隱藏層
輸出層,?
每層W和B之間的一組權重和偏差
為每個隱藏層選擇激活函數σ。在本教程中,我們將使用Sigmoid激活函數。
下圖顯示了2層神經網絡的體系結構(請注意,在計算神經網絡中的層數時通常會排除輸入層)
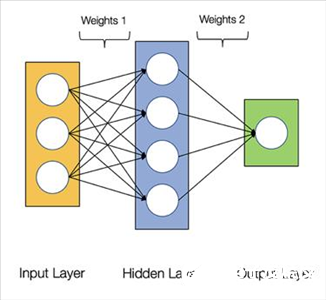
2層神經網絡的體系結構
用Python創建一個神經網絡類很容易。
神經網絡訓練
簡單的2層神經網絡的輸出是:
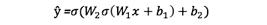
您可能會注意到,在上面的等式中,權重W和偏差b是影響?的唯一變量。
當然,權重和偏差的正確度決定了預測的準確性。從輸入數據中微調權重和偏差的過程稱為神經網絡訓練。
訓練過程的每次迭代包含以下步驟:
計算預測輸出?,稱為前饋
更新權重和偏差,稱為反向傳播
下圖為過程順序圖。

前饋
正如我們在上面的順序圖中看到的,前饋只是一個簡單的演算,對于基本的2層神經網絡,神經網絡的輸出是:
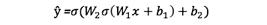
可以在python代碼中添加一個前饋函數來做到這一點。簡單起見,使假設偏差為0。
然而,仍然需要一種方法來評估我們預測達到什么程度,損失函數可以做到這一點。
損失函數
損失函數有很多種,問題的性質決定該選擇哪種損失函數。在本教程中,作者將使用一個簡單的sqaures偏差作為損失函數。

也就是說,平方和誤差僅僅是每個預測值和實際值之差的平均值。因為差值被平方,所以要測量差值的絕對值。
作者的訓練目標是找到最佳的權重和偏差集合,以最大限度地減少損失函數。
反向傳播
現在作者已經測量了預測誤差,需要找到一種方法來傳播誤差,并更新權重和偏差。
為了適當的調整權重和偏差,需要知道損失函數關于權重和偏差的導數。
可以從演算中得知,函數的導數就是函數的斜率。
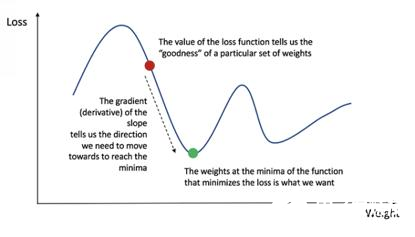
梯度下降算法
如果有導數,可以簡單地通過增加/減少更新權重和偏差(參見上圖)。這被稱為梯度下降。
然而,我們不能直接計算損失函數的權重和偏差,因為損失函數的方程不包含權重和偏差。因此,我們需要鏈式規則來計算它。
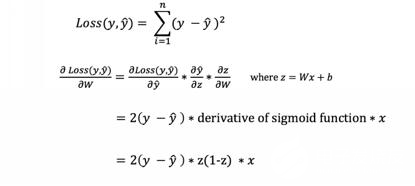
鏈式規則用于計算損失函數相對于權重的導數。簡單起見,只顯示了假設1層神經網絡的偏導數
得到相對于權重的損失函數的導數(斜率),以便適當調整權重。
現在,將反向傳播函數添加到Python代碼中。
為了深入理解演算的應用和反向傳播中的鏈式規則,作者強烈推薦3Blue1Brown撰寫教程。
結合在一起
現在已經有了完整的python代碼來做前饋和反向傳播,將神經網絡應用于一個例子上,來看看它的完成度。
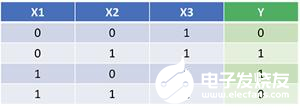
神經網絡應該學習理想的權重集合來表示這個函數。注意,通過檢查來計算權重并不是不重要的。
來看看訓練神經網絡進行1500次迭代后會發生什么。查看下面每個迭代圖的損失,可以清楚地看到損耗單調遞減到最小。這與之前的梯度下降算法一致。
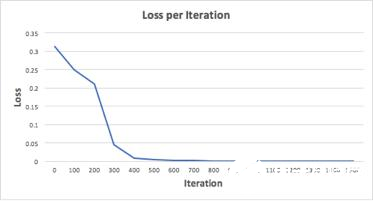
1500次迭代后神經網絡的最終預測(輸出)。
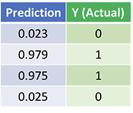
從上圖可以看出前饋和后向傳播算法成功地訓練了神經網絡,并且預測與實際值相差不大。
請注意,預測和實際值之間可以存在細微的差異。因為它可以防止過擬合,使神經網絡更好地歸納看不見的數據。
下一步是什么?
幸運的是,關于神經網絡和深度學習還有很多需要了解的內容。例如:
除了Sigmoid函數,還可以使用哪些激活函數?
訓練神經網絡時的學習率
利用卷積進行圖像分類任務
最后的想法
作者從頭開始學習了神經網絡。
盡管TensorFlow和Keras等深度學習庫可以在不完全了解神經網絡的內部工作的情況下輕松構建深度網絡,但有抱負的數據科學家可以更深入地了解神經網絡。
-
神經網絡
+關注
關注
42文章
4777瀏覽量
100958 -
函數
+關注
關注
3文章
4344瀏覽量
62809 -
python
+關注
關注
56文章
4801瀏覽量
84867
發布評論請先 登錄
相關推薦




 從零開始建立一個神經網絡
從零開始建立一個神經網絡










評論