題目描述
給出 n 代表生成括號的對數,請你寫出一個函數,使其能夠生成所有可能的并且有效的括號組合。
例如,給出 n = 3,生成結果為:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ] 題目解析
方法一:回溯算法(深度優先遍歷)
如果完成一件事情有很多種方法,并且每一種方法分成若干步驟,那多半就可以使用“回溯”算法完成。
“回溯”算法的基本思想是“嘗試搜索”,一條路如果走不通(不能得到想要的結果),就回到上一個“路口”,嘗試走另一條路。
因此,“回溯”算法的時間復雜度一般不低。如果能提前分析出,走這一條路并不能得到想要的結果,可以跳過這個分支,這一步操作叫“剪枝”。
做“回溯”算法問題的基本套路是:
1、使用題目中給出的示例,畫樹形結構圖,以便分析出遞歸結構;
一般來說,樹形圖不用畫完,就能夠分析出遞歸結構和解題思路。
2、分析一個結點可以產生枝葉的條件、遞歸到哪里終止、是否可以剪枝、符合題意的結果在什么地方出現(可能在葉子結點,也可能在中間的結點);
3、完成以上兩步以后,就要編寫代碼實現上述分析的過程,使用代碼在畫出的樹形結構上搜索符合題意的結果。
在樹形結構上搜索結果集,使用的方法是執行一次“深度優先遍歷”。在遍歷的過程中,可能需要使用“狀態變量”。
(“廣度優先遍歷”當然也是可以的,請參考方法二。)
我們以 n = 2 為例,畫樹形結構圖。
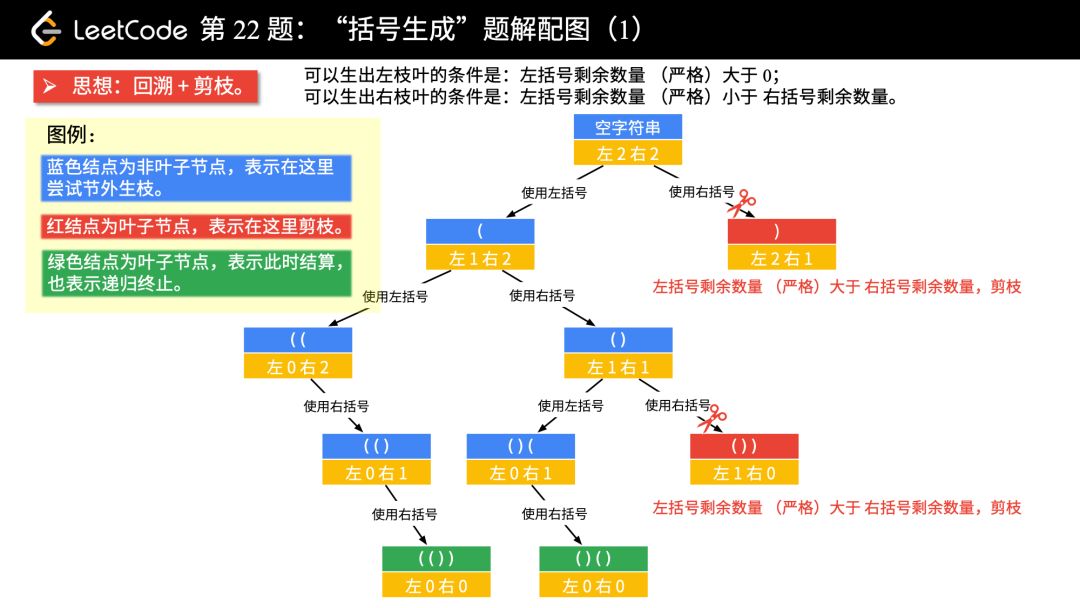
題解配圖(1)
畫圖以后,可以分析出的結論:
左右都有可以使用的括號數量,即嚴格大于 0 的時候,才產生分支;
左邊不受右邊的限制,它只受自己的約束;
右邊除了自己的限制以外,還收到左邊的限制,即:右邊剩余可以使用的括號數量一定得在嚴格大于左邊剩余的數量的時候,才可以“節外生枝”;
在左邊和右邊剩余的括號數都等于 0 的時候結算。
參考代碼如下:
publicclassSolution{ publicList
如果我們不用減法,使用加法,即 left 表示“左括號還有幾個沒有用掉”,right 表示“右括號還有幾個沒有用掉”,可以畫出另一棵遞歸樹。
題解配圖(2)
參考代碼如下:
publicclassSolution{ //方法 2:用加法 publicList
方法二:廣度優先遍歷
還是上面的題解配圖(1),使用廣度優先遍歷,結果集都在最后一層,即葉子結點處得到所有的結果集,編寫代碼如下。
publicclassSolution{ classNode{ /** *當前得到的字符串 */ privateStringres; /** *剩余左括號數量 */ privateintleft; /** *剩余右括號數量 */ privateintright; publicNode(Stringres,intleft,intright){ this.res=res; this.left=left; this.right=right; } @Override publicStringtoString(){ return"Node{"+ "res='"+res+'''+ ",left="+left+ ",right="+right+ '}'; } } publicList
方法三:動態規劃
第 1 步:定義狀態 dp[i]
使用 i 對括號能夠生成的組合。
注意:每一個狀態都是列表的形式。
第 2 步:狀態轉移方程:
i 對括號的一個組合,在 i - 1 對括號的基礎上得到;
i 對括號的一個組合,一定以左括號 "(" 開始(不一定以 ")" 結尾),為此,我們可以枚舉右括號 ")" 的位置,得到所有的組合;
枚舉的方式就是枚舉左括號 "(" 和右括號 ")" 中間可能的合法的括號對數,而剩下的合法的括號對數在與第一個左括號 "(" 配對的右括號 ")" 的后面,這就用到了以前的狀態。
狀態轉移方程是:
dp[i] = "(" + dp[可能的括號對數] + ")" + dp[剩下的括號對數]
“可能的括號對數” 與 “剩下的括號對數” 之和得為 i,故“可能的括號對數” j 可以從 0 開始,最多不能超過 i, 即 i - 1;
“剩下的括號對數” + j = i - 1,故 “剩下的括號對數” = i - j - 1。
整理得:
dp[i] = "(" + dp[j] + ")" + dp[i- j - 1] , j = 0, 1, ..., i - 1
第 3 步:思考初始狀態和輸出:
初始狀態:因為我們需要 0 對括號這種狀態,因此狀態數組 dp 從 0 開始,0 個括號當然就是 [""]。
1、自底向上:從小規模問題開始,逐漸得到大規模問題的解集;
2、無后效性:后面的結果的得到,不會影響到前面的結果。
publicclassSolution{ //把結果集保存在動態規劃的數組里 publicList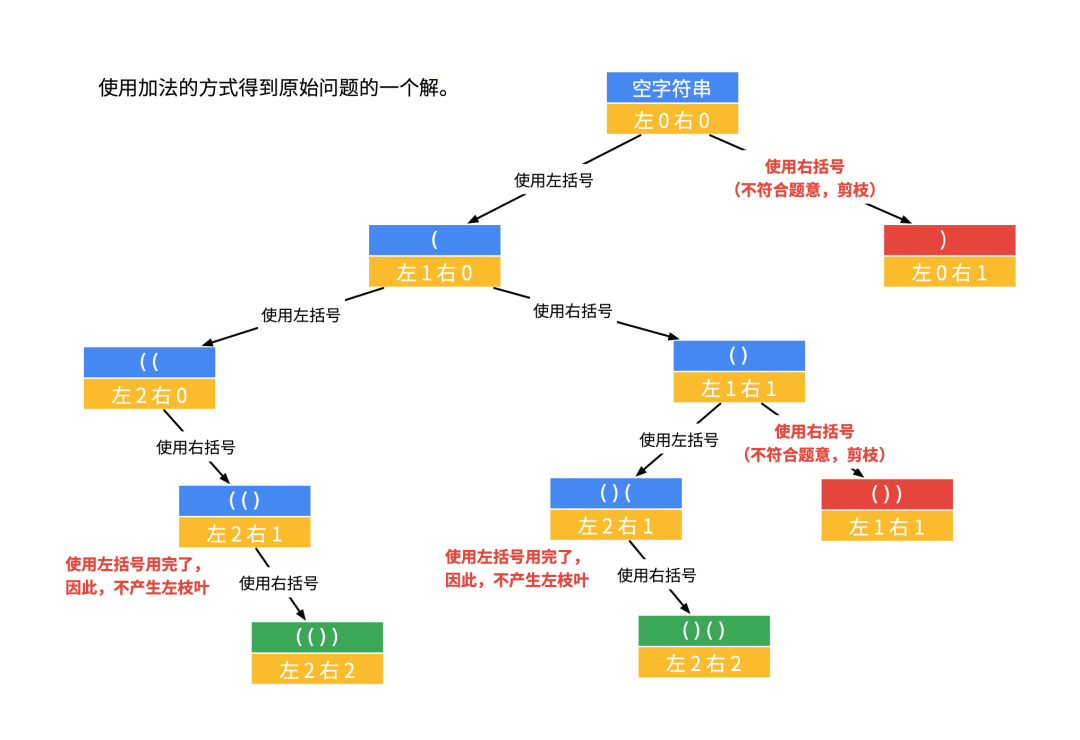
輸出:dp[n] 。
這個方法暫且就叫它動態規劃,這么用也是很神奇的,它有下面兩個特點:
-
算法
+關注
關注
23文章
4625瀏覽量
93129 -
遞歸
+關注
關注
0文章
29瀏覽量
9042
原文標題:超詳細!詳解一道高頻算法題:括號生成
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
硬件工程師面試常考的一道題,講講運算放大器的增益帶寬積

ADS1256 8通道依次采樣,數據不正確怎么解決?
AIGC算法解析及其發展趨勢
企業如何數字化轉型
好未來與微軟開展合作,攜手構建智慧學習生態系統
工商業儲能選型指南及參數詳解





 詳解一道高頻算法題:括號生成
詳解一道高頻算法題:括號生成











評論