今天我們要聊的這道題「Burst Balloon」和之前我們寫過的那篇 經典動態規劃：高樓扔雞蛋問題 分析過的高樓扔雞蛋問題類似，知名度很高，但難度確實也很大。因此 labuladong 公眾號就給這道題賜個座，來看一看這道題目到底有多難。

它是 LeetCode 第 312 題，題目如下：

title

首先必須要說明，這個題目的狀態轉移方程真的比較巧妙，所以說如果你看了題目之后完全沒有思路恰恰是正常的。雖然最優答案不容易想出來，但基本的思路分析是我們應該力求做到的。所以本文會先分析一下常規思路，然后再引入動態規劃解法。

一、回溯思路

先來順一下解決這種問題的套路：

我們前文多次強調過，很顯然只要涉及求最值，沒有任何奇技淫巧，一定是窮舉所有可能的結果，然后對比得出最值。

所以說，只要遇到求最值的算法問題，首先要思考的就是：如何窮舉出所有可能的結果？

窮舉主要有兩種算法，就是回溯算法和動態規劃，前者就是暴力窮舉，而后者是根據狀態轉移方程推導「狀態」。

如何將我們的扎氣球問題轉化成回溯算法呢？這個應該不難想到的，我們其實就是想窮舉戳氣球的順序，不同的戳氣球順序可能得到不同的分數，我們需要把所有可能的分數中最高的那個找出來，對吧。

那么，這不就是一個「全排列」問題嘛，我們前文 回溯算法框架套路詳解 中有全排列算法的詳解和代碼，其實只要稍微改一下邏輯即可，偽碼思路如下：

intres=Integer.MIN_VALUE; /*輸入一組氣球，返回戳破它們獲得的最大分數*/ intmaxCoins(int[]nums){ backtrack(nums,0); returnres; } /*回溯算法的偽碼解法*/ voidbacktrack(int[]nums,intsocre){ if(nums為空){ res=max(res,score); return; } for(inti=0;i

回溯算法就是這么簡單粗暴，但是相應的，算法的效率非常低。這個解法等同于全排列，所以時間復雜度是階乘級別，非常高，題目說了nums的大小n最多為 500，所以回溯算法肯定是不能通過所有測試用例的。

二、動態規劃思路

這個動態規劃問題和我們之前的動態規劃系列文章相比有什么特別之處？為什么它比較難呢？

原因在于，這個問題中我們每戳破一個氣球nums[i]，得到的分數和該氣球相鄰的氣球nums[i-1]和nums[i+1]是有相關性的。

我們前文動態規劃套路框架詳解 說過運用動態規劃算法的一個重要條件：子問題必須獨立。所以對于這個戳氣球問題，如果想用動態規劃，必須巧妙地定義dp數組的含義，避免子問題產生相關性，才能推出合理的狀態轉移方程。

如何定義dp數組呢，這里需要對問題進行一個簡單地轉化。題目說可以認為nums[-1] = nums[n] = 1，那么我們先直接把這兩個邊界加進去，形成一個新的數組points：

intmaxCoins(int[]nums){ intn=nums.length; //兩端加入兩個虛擬氣球 int[]points=newint[n+2]; points[0]=points[n+1]=1; for(inti=1;i<=?n;?i++)?{ ????????points[i]?=?nums[i?-?1]; ????} ????//?... }

現在氣球的索引變成了從1到n，points[0]和points[n+1]可以認為是兩個「虛擬氣球」。

那么我們可以改變問題：在一排氣球points中，請你戳破氣球0和氣球n+1之間的所有氣球（不包括0和n+1），使得最終只剩下氣球0和氣球n+1兩個氣球，最多能夠得到多少分？

現在可以定義dp數組的含義：

dp[i][j] = x表示，戳破氣球i和氣球j之間（開區間，不包括i和j）的所有氣球，可以獲得的最高分數為x。

那么根據這個定義，題目要求的結果就是dp[0][n+1]的值，而 base case 就是dp[i][j] = 0，其中0 <= i <= n+1, j <= i+1，因為這種情況下，開區間(i, j)中間根本沒有氣球可以戳。

//basecase已經都被初始化為0 int[][]dp=newint[n+2][n+2];

現在我們要根據這個dp數組來推導狀態轉移方程了，根據我們前文的套路，所謂的推導「狀態轉移方程」，實際上就是在思考怎么「做選擇」，也就是這道題目最有技巧的部分：

不就是想求戳破氣球i和氣球j之間的最高分數嗎，如果「正向思考」，就只能寫出前文的回溯算法；我們需要「反向思考」，想一想氣球i和氣球j之間最后一個被戳破的氣球可能是哪一個？

其實氣球i和氣球j之間的所有氣球都可能是最后被戳破的那一個，不防假設為k。回顧動態規劃的套路，這里其實已經找到了「狀態」和「選擇」：i和j就是兩個「狀態」，最后戳破的那個氣球k就是「選擇」。

根據剛才對dp數組的定義，如果最后一個戳破氣球k，dp[i][j]的值應該為：

dp[i][j]=dp[i][k]+dp[k][j] +points[i]*points[k]*points[j]

你不是要最后戳破氣球k嗎？那得先把開區間(i, k)的氣球都戳破，再把開區間(k, j)的氣球都戳破；最后剩下的氣球k，相鄰的就是氣球i和氣球j，這時候戳破k的話得到的分數就是points[i]*points[k]*points[j]。

那么戳破開區間(i, k)和開區間(k, j)的氣球最多能得到的分數是多少呢？嘿嘿，就是dp[i][k]和dp[k][j]，這恰好就是我們對dp數組的定義嘛！

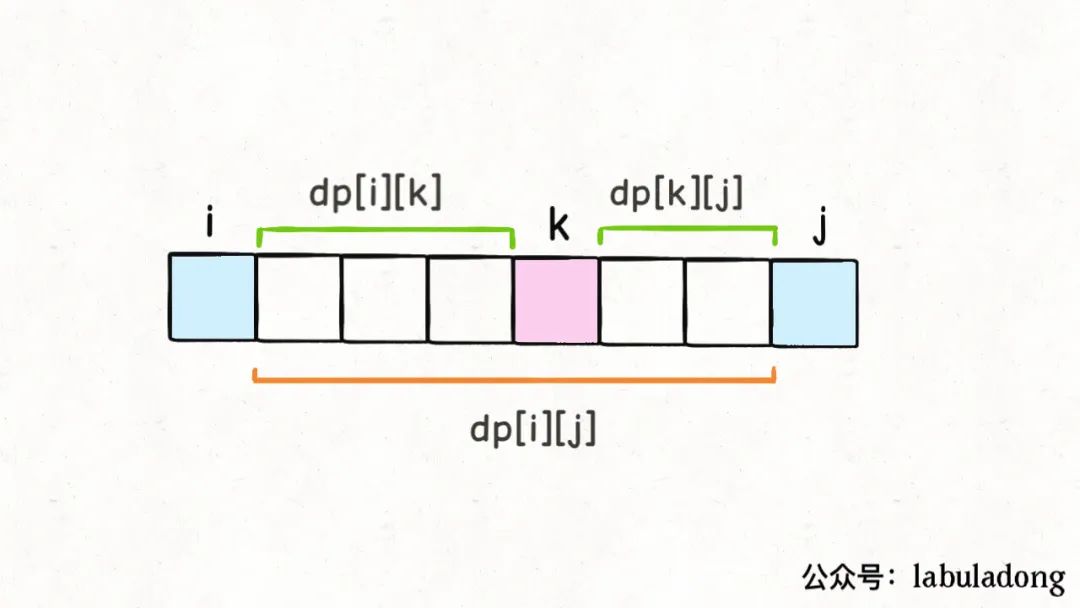
結合這個圖，就能體會出dp數組定義的巧妙了。由于是開區間，dp[i][k]和dp[k][j]不會影響氣球k；而戳破氣球k時，旁邊相鄰的就是氣球i和氣球j了，最后還會剩下氣球i和氣球j，這也恰好滿足了dp數組開區間的定義。

那么，對于一組給定的i和j，我們只要窮舉i < k < j的所有氣球k，選擇得分最高的作為dp[i][j]的值即可，這也就是狀態轉移方程：

//最后戳破的氣球是哪個？ for(intk=i+1;k

寫出狀態轉移方程就完成這道題的一大半了，但是還有問題：對于k的窮舉僅僅是在做「選擇」，但是應該如何窮舉「狀態」i和j呢？

for(inti=...;;) for(intj=...;;) for(intk=i+1;k

三、寫出代碼

關于「狀態」的窮舉，最重要的一點就是：狀態轉移所依賴的狀態必須被提前計算出來。

拿這道題舉例，dp[i][j]所依賴的狀態是dp[i][k]和dp[k][j]，那么我們必須保證：在計算dp[i][j]時，dp[i][k]和dp[k][j]已經被計算出來了（其中i < k < j）。

那么應該如何安排i和j的遍歷順序，來提供上述的保證呢？我們前文 動態規劃答疑篇 寫過處理這種問題的一個雞賊技巧：根據 base case 和最終狀態進行推導。

PS：最終狀態就是指題目要求的結果，對于這道題目也就是dp[0][n+1]。

我們先把 base case 和最終的狀態在 DP table 上畫出來：

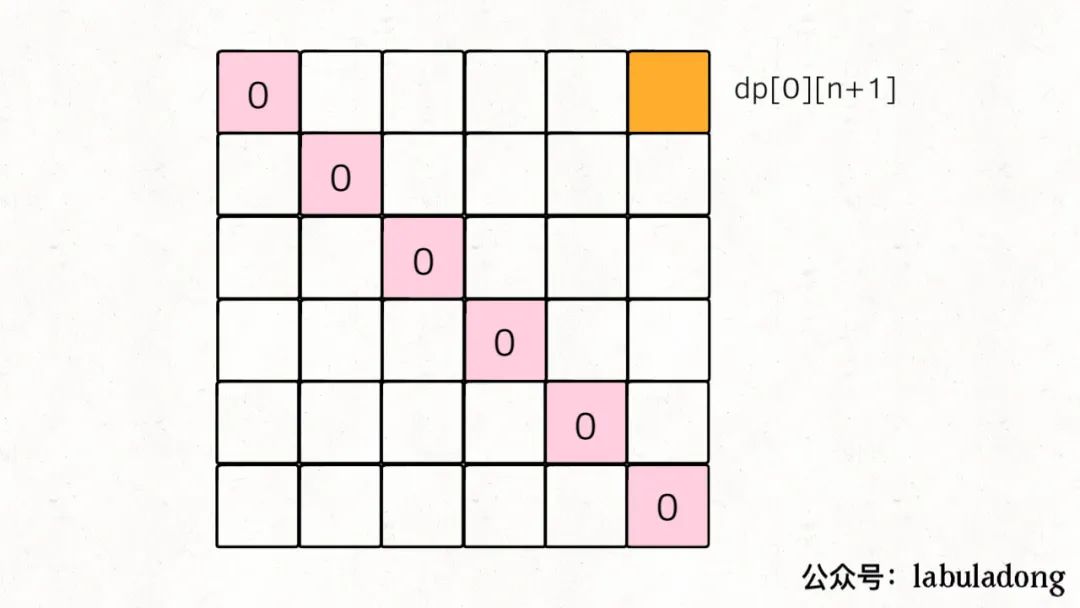
對于任一dp[i][j]，我們希望所有dp[i][k]和dp[k][j]已經被計算，畫在圖上就是這種情況：

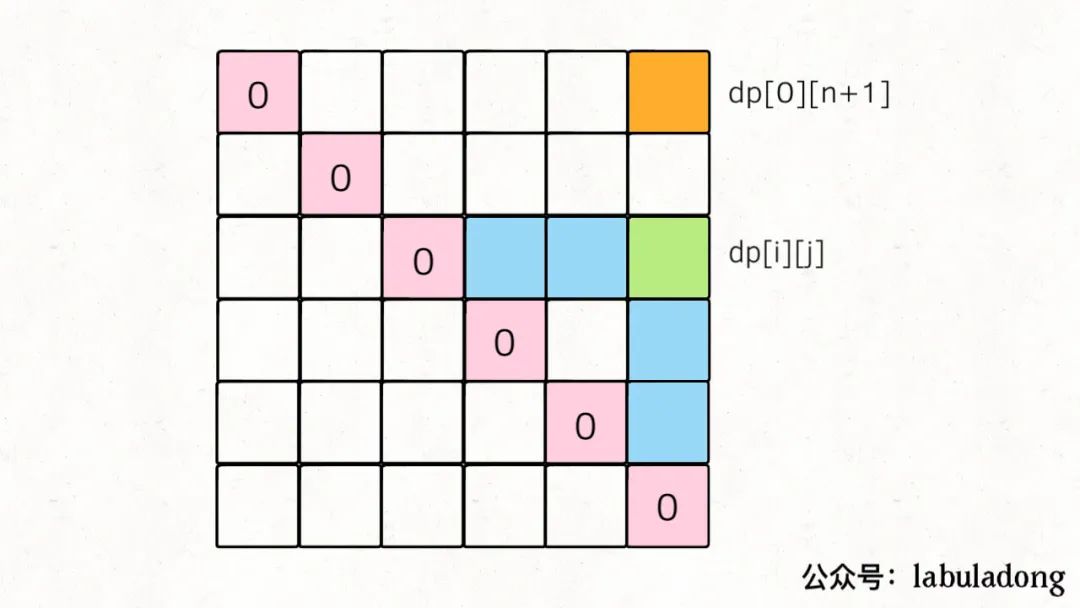
那么，為了達到這個要求，可以有兩種遍歷方法，要么斜著遍歷，要么從下到上從左到右遍歷：

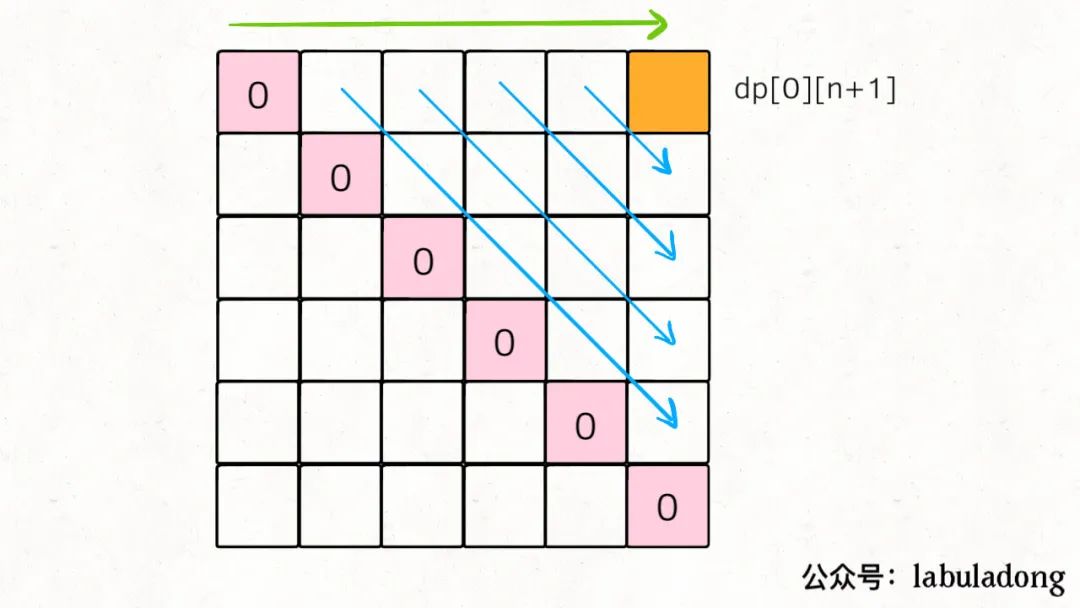
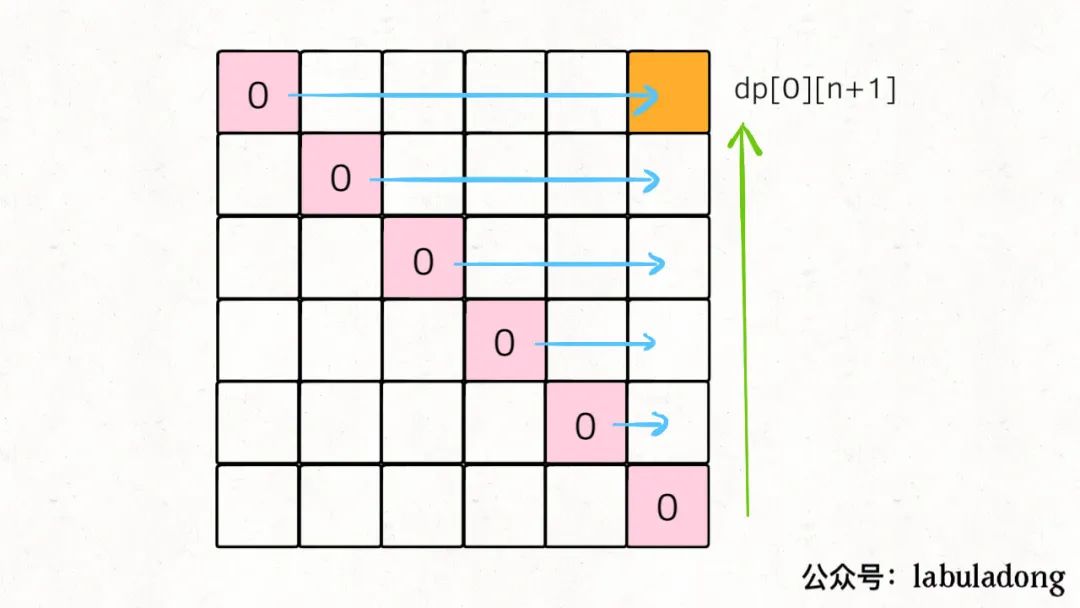
斜著遍歷有一點難寫，所以一般我們就從下往上遍歷，下面看完整代碼：

intmaxCoins(int[]nums){ intn=nums.length; //添加兩側的虛擬氣球 int[]points=newint[n+2]; points[0]=points[n+1]=1; for(inti=1;i<=?n;?i++)?{ ????????points[i]?=?nums[i?-?1]; ????} ????//?base?case?已經都被初始化為?0 ????int[][]?dp?=?new?int[n?+?2][n?+?2]; ????//?開始狀態轉移 ????//?i?應該從下往上 ????for?(int?i?=?n;?i?>=0;i--){ //j應該從左往右 for(intj=i+1;j

至此，這道題目就完全解決了，十分巧妙，但也不是那么難，對吧？

關鍵在于dp數組的定義，需要避免子問題互相影響，所以我們反向思考，將dp[i][j]的定義設為開區間，考慮最后戳破的氣球是哪一個，以此構建了狀態轉移方程。

對于如何窮舉「狀態」，我們使用了小技巧，通過 base case 和最終狀態推導出i,j的遍歷方向，保證正確的狀態轉移。