問題描述：

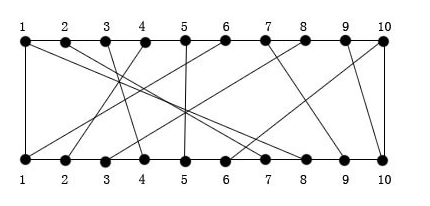
在一塊電路板的上、下兩端分別有n個接線柱。根據電路設計，要求用導線（i，π（i）） 將上端接線柱i與下端接線柱π（i）相連，如下圖。其中，π（i），1≤ i ≤n，是｛1，2，…，n｝的一個排列。導線（I， π（i））稱為該電路板上的第i條連線。對于任何1 ≤ i ≤ j ≤n，第i條連線和第j條連線相交的充要條件是π（i）》 π（j）。

π（i）=｛8，7，4，2，5，1，9，3，10，6｝

在制作電路板時，要求將這n條連線分布到若干絕緣層上。在同一層上的連線不相交。電路布線問題要確定將哪些連線安排在第一層上，使得該層上有盡可能多的連線。換句話說，該問題要求確定導線集Nets = ｛i，π（i），1 ≤ i ≤ n｝的最大的一個子集，這個子集中的導線互相不相交。

問題分析：

顯然這是一個組合問題，對于組合問題中求最優解的方法基本都是動態規劃算法。現在表述一下如何劃分子問題：

用B（i，j）表示最優解，其中，i是上端接線柱的序號，j是下端接線柱的序號，B（i，j）表示序號小于或等于i的上端接線柱和序號小于或等于j的下端接線柱中不相交連線的最大集合。 用size（i，j）表示集合中導線的數目（size（i，j）=|B（i，j）|）。B（i，j）的值蘊含在B（i-1，j）和B（i，j-1）這倆個子問題中，對于有2xN個接線柱的電路板，那么B（N，N）就是其解了。

對于上端接線柱t，用 π（t）表示與他相連的下端接線柱

那么遞推公式為：

遞推公式證明：

對于從B（i-1，j）或B（i，j-1）到B（i，j）要么會多加一條導線，要么不加。

1. 當 j==π（i）時，（i，j）則是一條導線，且這條導線對B（i-1，j-1）的值沒有影響，因為B（i-1，j-1）中的任意的一條導線的節點序號（無論是上端節點序號還是下端節點序號）都小于i，j，這由其空間位置決定的。

現在求B（i，j）， 即求序號小于或等于i的上端接線柱和序號小于或等于j的下端接線柱中不相交導線的最大集合。顯然應是B（i-1，j-1）U（i，j）。

2 。 當j！= π（i）時。假如問題是從B（i，j-1）到B（i，j），那么下端新加入的接線柱j要么與上端的1至i-1個接線柱構成導線（與第i個接線柱構成導線的情況在上面已經討論），要么不構成。

如果構成的話那么這種情況其實已經在B（i-1，j）中討論了，這里不再考慮。那么B（i，j） 應是序號區間比他小一點的子問題的解。小一點是多少，肯定就是少一個接線柱了，也就是B（i-1，j）。

如果不構成的話，那么B（i，j）肯定就是序號區間比他小一點的子問題的解了。

對于B（i，j）可能由B（i-1，j）或B（i，j-1）過渡而來，所以B（i，j）取其中較大的一個。