今天分享的題目來源于 LeetCode 第 450 號問題:刪除二叉搜索樹中的節點。雖然它的難度是中等,但實際上很好理解,請往下看!
題目描述
給定一個二叉搜索樹的根節點root和一個值key,刪除二叉搜索樹中的key對應的節點,并保證二叉搜索樹的性質不變。返回二叉搜索樹(有可能被更新)的根節點的引用。
一般來說,刪除節點可分為兩個步驟:
首先找到需要刪除的節點;
如果找到了,刪除它。
說明:要求算法時間復雜度為 O(h),h 為樹的高度。
示例:
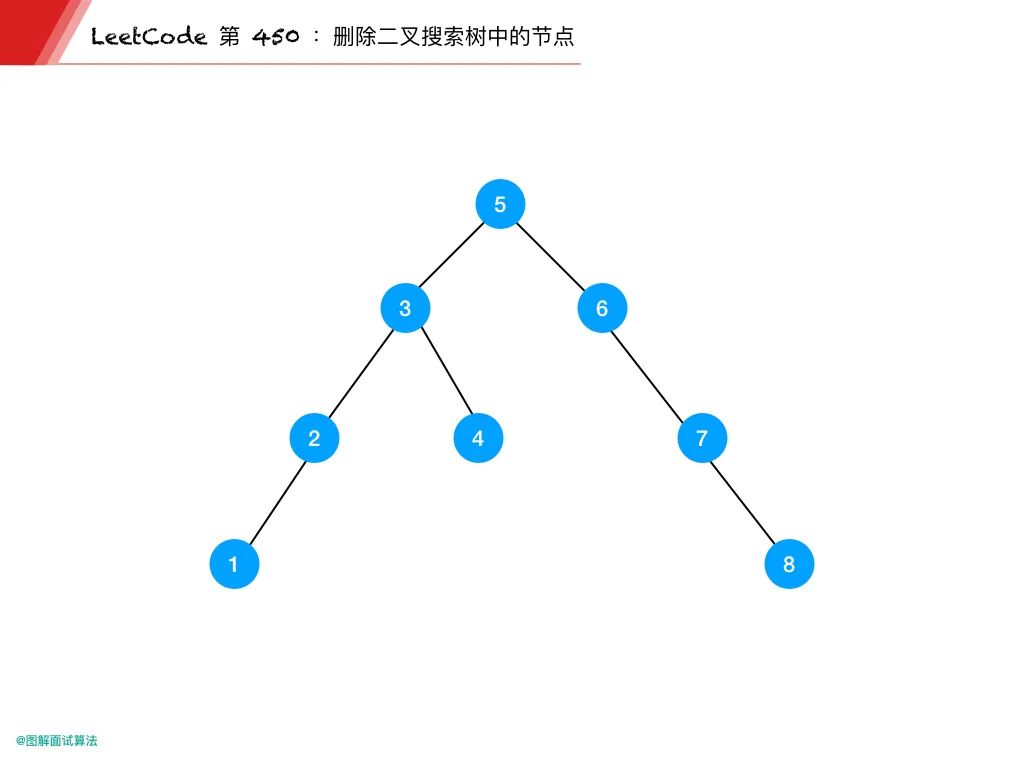
root=[5,3,6,2,4,null,7] key=3 5 / 36 / 247 給定需要刪除的節點值是3,所以我們首先找到3這個節點,然后刪除它。 一個正確的答案是[5,4,6,2,null,null,7], 如下圖所示。 5 / 46 / 27 另一個正確答案是[5,2,6,null,4,null,7]。 5 / 26 47
題目解析
在二叉搜索樹上刪除一個節點,這道題目有一個隱含的條件,就是樹上節點的值不重復。
另外題目還要求時間復雜度需要保證 O(h) 這里的 h 表示的是二叉樹的高度。
其實這個題目是分成兩個步驟的,第一個是找到對應的節點,第二個是刪除節點。
因為是二叉搜索樹,對于樹上每個節點來說,其右子樹的節點都要大于其左子樹的節點,那么要找對應節點,我們可以從根節點開始,一路比較,大的話就去右邊找,小的話就去左邊找,這樣每次我們都往下,可以保證時間復雜度是 O(h)。
當我們找到了要刪除的節點,在刪除這一步就會有很多的細節,主要是因為我們需要調整余下的結構,以維持二叉搜索樹的性質。
針對這個問題,我們可以分情況討論:
5 / 36 / 247 / 18
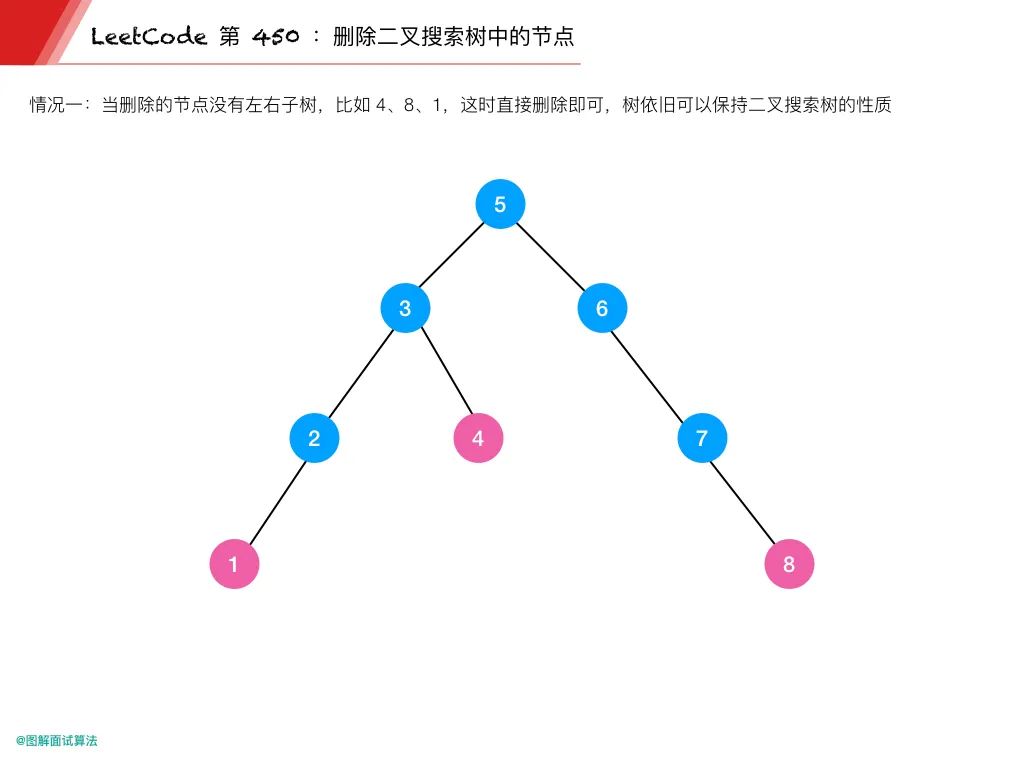
情況 1:當刪除的節點沒有左右子樹,比如上圖的 4、8、1
這時直接刪除即可,樹依舊可以保持二叉搜索樹的性質
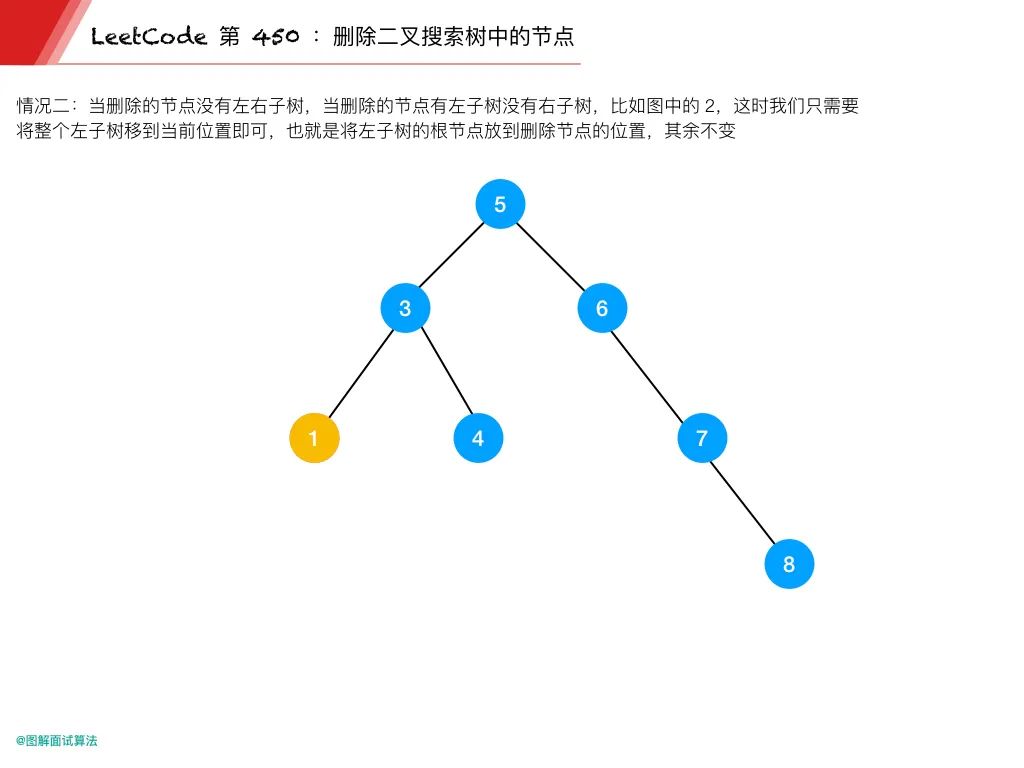
情況 2:當刪除的節點有左子樹沒有右子樹,比如上圖的 2
這時我們只需要將整個左子樹移到當前位置即可
也就是將左子樹的根節點放到刪除節點的位置,其余不變
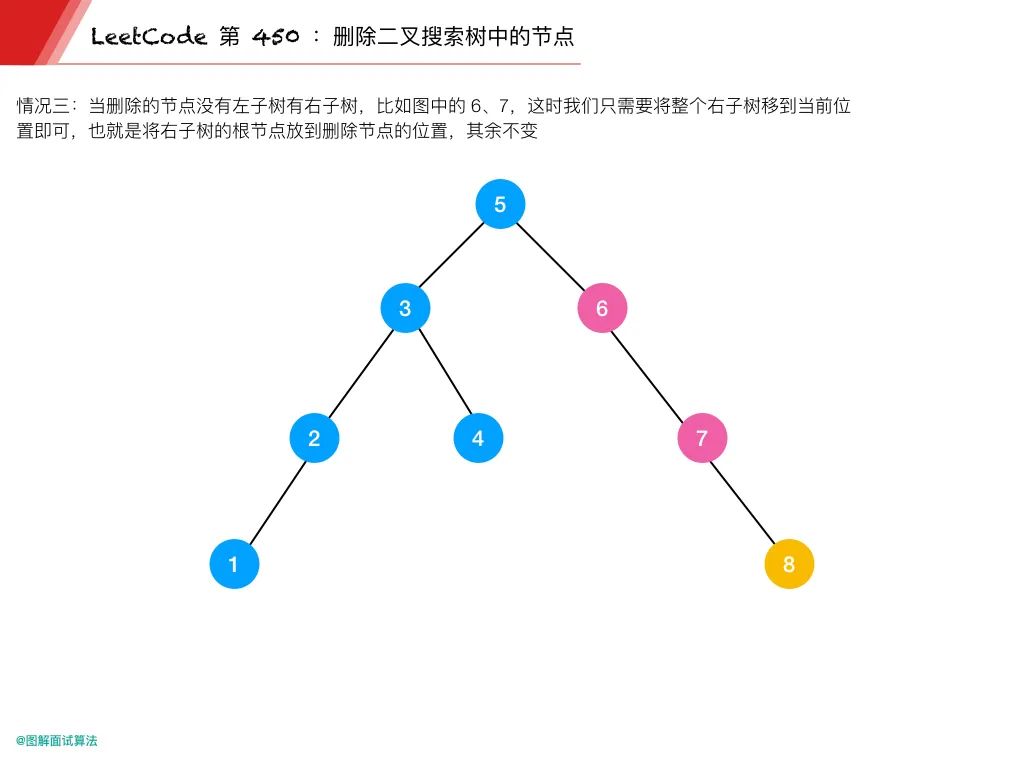
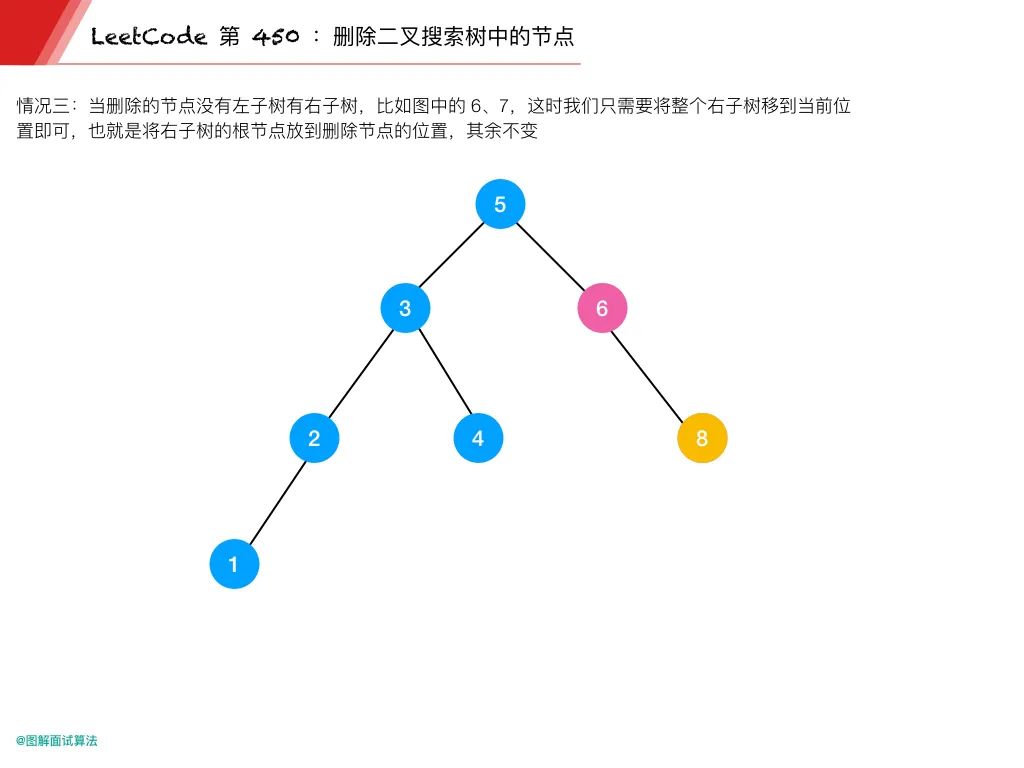
情況 3:當刪除的節點沒有左子樹有右子樹,比如上圖的 6、7
這時我們只需要將整個右子樹移到當前位置即可
也就是將右子樹的根節點放到刪除節點的位置,其余不變
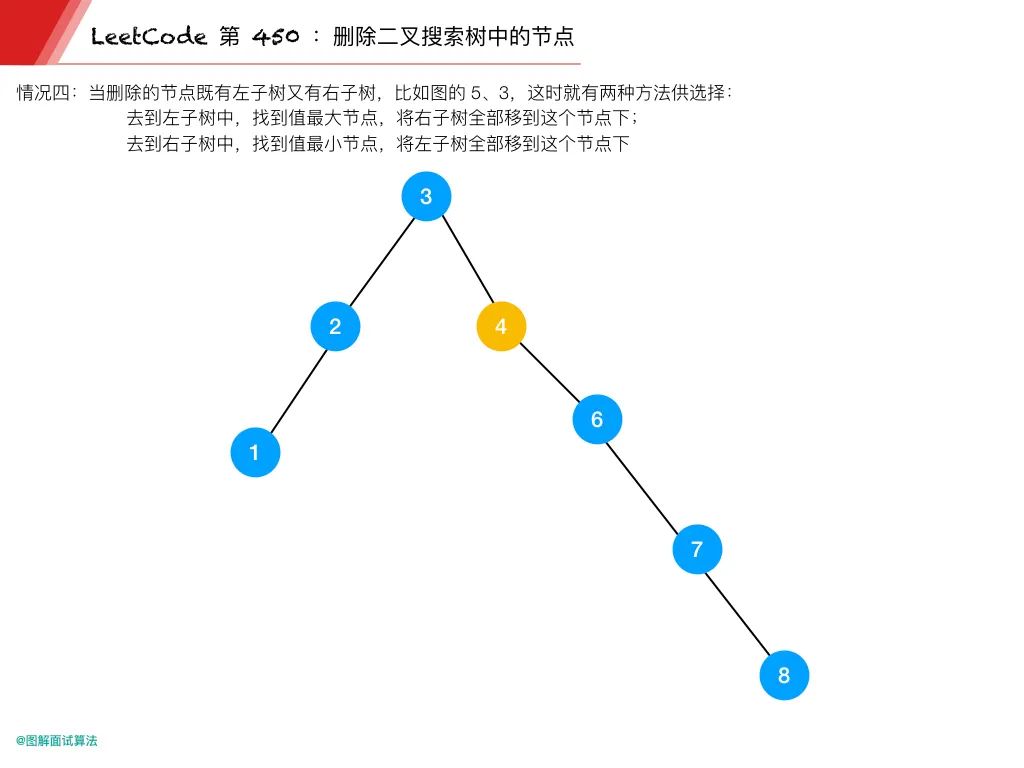
情況 4:當刪除的節點既有左子樹又有右子樹,比如上圖的 5、3
這時就有兩種方法供選擇:
去到左子樹中,找到值最大節點,將右子樹全部移到這個節點下
去到右子樹中,找到值最小節點,將左子樹全部移到這個節點下
通過上面的討論分析,我們有了大致的思路。在實現方面,我們可以借助遞歸來巧妙地達到刪除對應節點的目的。
圖片描述




參考代碼
//五分鐘學算法 publicTreeNodedeleteNode(TreeNoderoot,intkey){ if(root==null){ returnnull; } //當前遍歷到的節點大于要找的節點,去左邊繼續找 if(root.val>key){ root.left=deleteNode(root.left,key); } //當前遍歷到的節點小于要找的節點,去右邊繼續找 elseif(root.val
-
算法
+關注
關注
23文章
4625瀏覽量
93129 -
二叉樹
+關注
關注
0文章
74瀏覽量
12357
原文標題:五分鐘看懂一道中等難度的算法題
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
嵌入式學習-飛凌嵌入式ElfBoard ELF 1板卡-初識設備樹之設備樹組成和結構
飛凌嵌入式ElfBoard ELF 1板卡-初識設備樹之設備樹組成和結構
谷歌取消“站點鏈接搜索框”,適應新搜索需求
邏輯組件中的流程塊節點通常出于什么用途
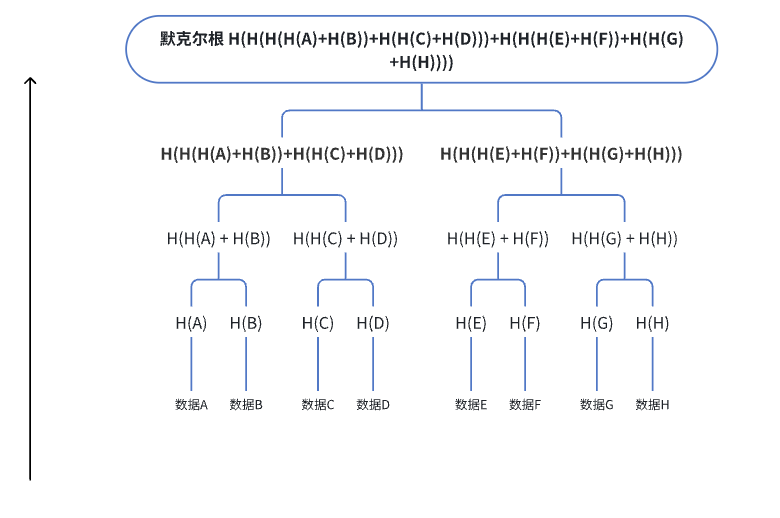
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?




 刪除二叉搜索樹中的節點
刪除二叉搜索樹中的節點










評論