如果你對(duì)信號(hào)處理感興趣,說(shuō)一天征服傅里葉有點(diǎn)夸張。當(dāng)然,沒(méi)有反覆實(shí)踐和鉆研數(shù)學(xué),您無(wú)法在一天里學(xué)會(huì)傅立葉變換的方方面面。無(wú)論如何, 這個(gè)在線課程將提供給您怎樣進(jìn)行傅立葉變換運(yùn)算的基本知識(shí)。
能有效和能非常簡(jiǎn)單地領(lǐng)會(huì)的原因是我們使用了一種不太傳統(tǒng)的逼近。重要的是你將學(xué)習(xí)傅立葉變換的要素而完全不用超過(guò)加法和乘法的數(shù)學(xué)計(jì)算! 我將設(shè)法在不超過(guò)以下六節(jié)里解釋在對(duì)音像信號(hào)處理中傅立葉變換的實(shí)際應(yīng)用。
步驟 1: 一些簡(jiǎn)單的前提
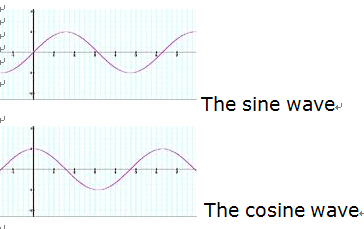
在下面,您需要理解以下四件最基本的事情: 加法,乘、除法。什么是正弦,余弦和正弦信號(hào)。明顯地,我將跳第一二件事和將解釋位最后一個(gè)。您大概還記得您在學(xué)校學(xué)過(guò)的“ 三角函數(shù)”[1] ,它神秘地用于 與角度一起從它們的內(nèi)角計(jì)算它們的邊長(zhǎng),反之亦然。我們這里不需要所有這些事,我們只需要知道二個(gè) 最重要的三角函數(shù),"正弦" 和"余弦" 的外表特征。這相當(dāng)簡(jiǎn)單: 他們看起來(lái)象是以峰頂和谷組成的從觀察點(diǎn)向左右無(wú)限伸展的非常簡(jiǎn)單的波浪。
(附圖一)
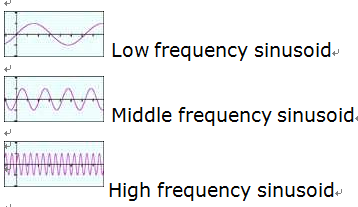
如同你所知道的,這兩種波形是周期性的,這意味著在一定的時(shí)間、周期之后,它們看起來(lái)再次一樣。兩種波形看起來(lái)也很象,但當(dāng)正弦波在零點(diǎn)開(kāi)始時(shí)余弦波開(kāi)始出現(xiàn)在最大值。在實(shí)踐中,我們?nèi)绾闻卸ㄎ覀冊(cè)谝粋€(gè)給定時(shí)間所觀測(cè)到的波形是開(kāi)始在它的最大值或在零? 問(wèn)的好: 我們不能。實(shí)踐上沒(méi)有辦法區(qū)分正弦波和余弦波,因此看起來(lái)象正弦或余弦波的我們統(tǒng)稱為正弦波,在希臘語(yǔ)中譯作"正弦類"。正弦波的一個(gè)重要性質(zhì)是"頻率"。它告訴我們?cè)谝粋€(gè)給定的時(shí)間內(nèi)有多少個(gè)波峰和波谷。高頻意味許多波峰和波谷, 低頻率意味少量波峰和波谷:
(附圖二)
步驟 2: 了解傅立葉定理
Jean-Baptiste Joseph Fourier 是孩子們中讓父母感到驕傲和慚愧的的一個(gè),因?yàn)樗臍q時(shí)就開(kāi)始對(duì)他們說(shuō)非常復(fù)雜的數(shù)學(xué)用語(yǔ)。他的一生中做了很多重要工作,但最重大的發(fā)現(xiàn)可能是解決了材料熱傳導(dǎo)問(wèn)題。
他推導(dǎo)出了描述熱在某一媒介中如何傳導(dǎo)的公式,即用三角函數(shù)的無(wú)窮級(jí)數(shù)來(lái)解決這個(gè)問(wèn)題(就是我們?cè)谏厦嬗懻撨^(guò)的正弦、余弦函數(shù))。主要和我們話題有關(guān)的是:傅里葉的發(fā)現(xiàn)總結(jié)成一般規(guī)律就是任意復(fù)雜的信號(hào)都能由一個(gè)個(gè)混合在一起的正弦函數(shù)的和來(lái)表示。
這是一個(gè)例子:

(附圖三)
在這里你看到的是一個(gè)原始的信號(hào),以及如何按某一確定的關(guān)系(“ 配方” )混合在一起的正弦函數(shù)混合物(我們稱它們?yōu)榉至浚┧平N覀儗⒑?jiǎn)略地談?wù)撘幌履欠菖浞健H缒闼覀冇玫恼液瘮?shù)愈多 其結(jié)果就愈精確地接近我們的原始信號(hào)波形。在“ 現(xiàn)實(shí)” 世界中,在信號(hào)連續(xù)的地方,即你能以無(wú)窮小的間 隔來(lái)測(cè)量它們,精度僅受你的測(cè)試設(shè)備限制,你需要無(wú)限多的正弦函數(shù)才能完美地建立任意一個(gè)給定的信 號(hào)。幸運(yùn)地是,和數(shù)字信號(hào)處理者們一樣,我們不是生活在那樣的世界。相反,我們將處理僅以有限精度 每隔一定間隔被測(cè)量的現(xiàn)實(shí)世界的采樣信號(hào)。因而,我們不需要無(wú)限多地正弦函數(shù),我們只需要非常多。稍后我們也將討論這個(gè)“ 非常多” 是多少。目前重要的一點(diǎn)是你能夠想象,任意一個(gè)在你計(jì)算機(jī)上的信號(hào), 都能用簡(jiǎn)單正弦波按配方組成。
步驟 3: “ 非常多” 是多少
正如我們所知道的,復(fù)雜形狀的波形能由混合在一起的正弦波所建立。我們也許要問(wèn)需要多少正弦波來(lái) 構(gòu)造任意一個(gè)在計(jì)算機(jī)上給定的信號(hào)。當(dāng)然,倘若我們知道正在處理的信號(hào)是如何組成的,這可能至少是 一個(gè)單個(gè)正弦波。在許多情況下,我們處理的現(xiàn)實(shí)世界的信號(hào)可能有非常復(fù)雜的結(jié)構(gòu),以至于我們不能深 入知道實(shí)際上有多少“ 分量” 波存在。在這種情況下,即使我們無(wú)法知道原始的信號(hào)是由多少個(gè)正弦波來(lái)構(gòu) 成的,肯定存在一個(gè)我們將需要多少正弦波的上限。盡管如此,這實(shí)際上沒(méi)解決有多少的問(wèn)題。讓我們?cè)?著來(lái)直觀地逼近它: 假設(shè)一個(gè)信號(hào)我們有 1000 個(gè)樣采,可能存在的最短周期正弦波(即多數(shù)波峰波谷在其 中)以交替的波峰波谷分布在每個(gè)采樣內(nèi)。因此,最高頻率的正弦波將有 500 個(gè)波峰和 500 個(gè)波谷在我 們的 1000 個(gè)采樣中,且每隔一個(gè)采樣是波峰。下圖中的黑點(diǎn)表示我們的采樣,所以,最高頻率的正弦波 以看起來(lái)象這樣:
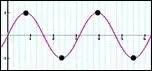
The highest frequency sine wave(附圖四)
現(xiàn)在讓我們來(lái)看一下最低頻率正弦波可能多么低。如果我們只給一個(gè)單獨(dú)的采樣點(diǎn),我們將如何能測(cè)量穿過(guò)這點(diǎn)的正弦波的峰頂和谷? 我們做不到,因?yàn)橛性S多不同周期正弦波穿過(guò)這點(diǎn)。
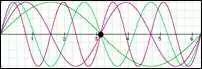
(附圖五)
所以,一個(gè)單獨(dú)數(shù)據(jù)點(diǎn)不足以告訴我們關(guān)于頻率的任何事。現(xiàn)在,如果我們有兩個(gè)采樣,那么穿過(guò)這 兩點(diǎn)的正弦波的最低頻率是什么?在這種情況下它很常簡(jiǎn)單。只有一個(gè)穿過(guò)這兩點(diǎn)的非常低頻率的正弦 波。它看起來(lái)向這樣:
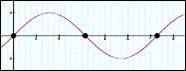
The lowest frequency sine wave(附圖六)
想象最左面的兩個(gè)點(diǎn)是二個(gè)釘子和一個(gè)跨越它們之間的弦(圖六描述三個(gè)數(shù)據(jù)點(diǎn)是因?yàn)檎也ǖ闹芷谛裕覀儗?shí)際上只需要最左面的兩點(diǎn)說(shuō)明它的頻率)。我們能領(lǐng)會(huì)的最低的頻率是來(lái)回地?cái)[動(dòng)在二個(gè)釘 子之間的弦,象是圖六中左邊兩點(diǎn)之間的正弦波所做的。如果我們有 1000 個(gè)采樣,那么兩個(gè)“ 釘子” 相當(dāng) 于第一個(gè)或最后的采樣,比如 1 號(hào)采樣和 1000 號(hào)采樣。從對(duì)樂(lè)器的體驗(yàn)我們知道,當(dāng)長(zhǎng)度增加時(shí)弦的頻 率將下降。所以我們可以想象,當(dāng)我們將兩個(gè)釘子向彼此遠(yuǎn)離的方向移開(kāi)時(shí),最小正弦波的頻率將變得更 低。例如,如果我們選擇 2000 個(gè)采樣,因?yàn)槲覀兊摹?釘子” ,在 1 號(hào)或 2000 號(hào)采樣間,所以最低正弦波將 更低。事實(shí)上,它將低兩倍,因?yàn)橐驗(yàn)槲覀兊尼斪颖?1000 個(gè)采樣時(shí)遠(yuǎn)兩倍。這樣,如果我們有更多的采 樣,我們將能辨別出一個(gè)更低頻率的正弦波,因?yàn)樗鼈兊牧憬徊纥c(diǎn)(我們的“ 釘子” )將移動(dòng)得更遠(yuǎn)。這對(duì) 了解下面的解釋是非常重要的。
象我們看到的那樣,在兩個(gè)“ 釘子” 之后,我們的波形開(kāi)始重復(fù)上升斜坡(第一個(gè)釘子和第三個(gè)釘子同樣)。這意味著任意兩個(gè)相鄰的釘子準(zhǔn)確地包含完整正弦波的一半,換句話說(shuō)一個(gè)峰或一個(gè)谷或半個(gè)周期。
概括一下我們剛學(xué)過(guò)的東西,我們知道,一個(gè)采樣正弦波的上限頻率是所有其它有一個(gè)波峰和波谷的 采樣,并且,低頻下限是我們看到的正好匹配采樣數(shù)的正弦波的周期的一半。但等一下,這難到不意味著, 當(dāng)上限頻率保持固定時(shí),當(dāng)有很多采樣時(shí)最低頻率可以降低?確實(shí)如此! 結(jié)果我們將從一個(gè)低頻開(kāi)始增加 更多正弦波來(lái)組成一個(gè)較長(zhǎng)的未知內(nèi)容的信號(hào)。
一切都清楚了,但我們?nèi)匀徊恢牢覀冏罱K需要多少正弦波。就象我們現(xiàn)在知道任意正弦波分量所能 具的有上下限頻率一樣,我們能計(jì)算出適合這兩個(gè)極限之間的量是多少。既然我們沿著最左到最右的采樣 固定了最低正弦波分量,我們要所有其它正弦波最好也使用這些釘子(為什么我們要不同地對(duì)待他們? 所有的正弦波被同等的創(chuàng)建!)。假設(shè)正弦波束是系在吉他上二個(gè)固定點(diǎn)的弦。它們能只搖擺在二個(gè)釘子之間(除非他們斷了),就象我們下圖的正弦波。這導(dǎo)致如下關(guān)系,我們的最低分量(1)以 1/2 周期裝配,第二分量(2)以 1 個(gè)周期裝配,第三分量以 1 1/2 周期裝配以此類推直到我們看到的 1000 個(gè)采樣。形象地, 看起來(lái)象這:
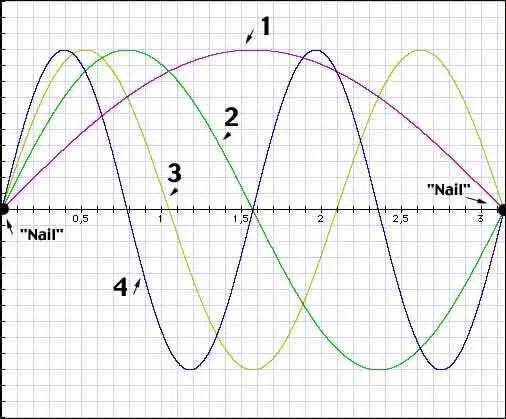
(附圖七)
在,如果我們算一下要多少正弦波以那種方法裝配我們的 1000 個(gè)采樣,就會(huì)發(fā)現(xiàn)我們精確地需要1000 個(gè)正弦波疊加起來(lái)表示 1000 個(gè)采樣。實(shí)際上,我們總是發(fā)現(xiàn)我們需要和采樣一樣多的正弦波。
步驟 4 關(guān)于烹飪食譜
在前面的段落我們看到, 任一個(gè)給定的在計(jì)算機(jī)上的信號(hào)能被正弦波混合物來(lái)構(gòu)造。我們考慮了他們的頻率,并且考慮了需要多大的最低和最高頻率的正弦波來(lái)完美地重建任一個(gè)我們所分析信號(hào)。我們明白 了為確定所需最低的正弦波分量,我們考察的采樣的數(shù)量是重要,但我們還未論述實(shí)際正弦波如何必需被 混合產(chǎn)生某一確定的結(jié)果。由疊加正弦波組成任何指定的信號(hào),我們需要測(cè)量他們的另外一個(gè)方面。實(shí)際 上,頻率不是我們需要知道的唯一的事。我們還需要知道正弦波的幅度,也就是說(shuō)每個(gè)正弦波幅度有多高 才能混合在一起產(chǎn)生我們需要的輸入信號(hào)。高度是正弦波的峰頂?shù)母叨龋饧捶屙敽土憔€之間距離。幅度 赿高,我們聽(tīng)到的聲音也就赿大。所以,如果您有一個(gè)含有許多低音的信號(hào),無(wú)疑可以預(yù)期混合體中的低 頻率正弦波的分量比例比高頻正弦波分量更大。因此一般情況下,低音中的低頻正弦波有一個(gè)比高頻正弦 波更高的幅度。在我們的分析中,我們將需要確定各個(gè)分量正弦波的幅度以完成我們的配方。
步驟 5:關(guān)于蘋果和桔子
如果你一直跟著我,我們幾乎完成了通向傅里葉變換的旅程。我們學(xué)了需要多少正弦波,它的數(shù)量依 賴于我們查看的采樣的數(shù)量有一個(gè)頻率上下限界,并且不知道怎么確定單個(gè)分量的幅度以完成我們的配 方。我們一直不清楚究竟如何從我們的采樣來(lái)確定實(shí)際的配方。直觀上我們可以斷定能找到正弦波的幅度, 設(shè)法把一個(gè)已知頻率正弦波和采樣作對(duì)比,我們測(cè)量找出它們有多么接近。如果它們精確地相等,我們知 道該正弦波存在著相同的幅度,如果我們發(fā)現(xiàn)我們的信號(hào)與參考正弦波一點(diǎn)也不匹配,我們將認(rèn)為這個(gè)不 存在。盡管如此,我們?nèi)绾胃咝У匕岩粋€(gè)已知的正弦波同采樣信號(hào)進(jìn)行比較?幸運(yùn)地是,數(shù)字信號(hào)處理工 作者早已解決了如何作這些。事實(shí)上,這象加法和乘法一樣容易-我們?nèi)∫粋€(gè)已知頻率的單位正弦波(這意味著它的振幅是 1,可從我們的計(jì)算器或計(jì)算機(jī)中精確地獲得)和我們的信號(hào)采樣相乘。累加乘積之后, 我們將得到我們正在觀測(cè)的這個(gè)頻率上正弦波分量的幅度。
這是個(gè)舉例,一個(gè)簡(jiǎn)單的完成這些工作的 C 代碼片段:
Listing 1.1: The direct realization of the Discrete Sine Transform (DST):
#define M_PI 3.14159265358979323846
long bin,k;
double arg;
for (bin = 0; bin < transformLength; bin++) {
transformData[bin] = 0.;
for (k = 0; k < transformLength; k++) {
arg = (float)bin * M_PI *(float)k / (float)transformLength;
transformData[bin] += inputData[k] * sin(arg);
}
}
這段代碼變換存儲(chǔ)在 inputData[0...transformLength-1]中我們測(cè)量的采樣點(diǎn)成為一個(gè)正弦波分量的幅度隊(duì)列 transformData[0...transformLength-1]。根據(jù)通用術(shù)語(yǔ),我們稱參考正弦波的頻率步長(zhǎng)為盒(bin),
這意味著它們被認(rèn)為象是一個(gè)我們放置我們估計(jì)的任意分量波的幅度的容器。離散正弦變換(DST)是一個(gè)普通程序,它假設(shè)我們無(wú)法想象我們的信號(hào)看起來(lái)象什么樣,否則我們能使用一個(gè)更加高效率的方法來(lái)確 定正弦波分量的幅度(例如,我們予先知道, 我們的信號(hào)是一個(gè)已知頻率的正弦波。我們能直接地找出它 的高度而不用計(jì)算正弦波的整個(gè)范圍。實(shí)現(xiàn)這個(gè)有效的逼近是基于傅里葉原理,它能在文獻(xiàn)的戈策爾(Goe rtzel)算法條目下找到)。
這些就是你堅(jiān)持想要的我們?yōu)槭裁从眠@樣的方法計(jì)算正弦變換的一個(gè)解釋:對(duì)我們用一個(gè)已知頻率正弦 波的乘積來(lái)作一種非常直觀逼近的理由,可以設(shè)想,這大致相當(dāng)于一個(gè)固有頻率的“ 共振” 在系統(tǒng)內(nèi)發(fā)生時(shí) 物理世界發(fā)生的事情。sin(arg)項(xiàng)本質(zhì)上是一個(gè)獲得由輸入信號(hào)波形激勵(lì)的諧振器。如果輸入(信號(hào))有在 我們正觀測(cè)的頻率上的分量,它的輸出將是參考正弦波諧振的幅度。因?yàn)槲覀兊膮⒖疾ㄊ菃挝环鹊模敵鍪且粋€(gè)在那個(gè)頻率上的分量的實(shí)際幅度的一個(gè)直接測(cè)量。因?yàn)橹C振器只是簡(jiǎn)單的濾波器,變換(不可否 認(rèn)是在稍微寬松條件下)被認(rèn)為有極窄的帶通濾波器組的特征,它位于我們估值的頻率中心的周圍。這有 助于解釋一個(gè)事實(shí),為什么傅立葉變換提供了對(duì)信號(hào)進(jìn)行過(guò)濾的一個(gè)高效工具。
只是為了完備性: 當(dāng)然,上述程序是可逆的,當(dāng)我們知道它的正弦波分量時(shí),我們的信號(hào)(在數(shù)字精確度 極限內(nèi))能完全被重建,通過(guò)簡(jiǎn)單地把正弦波加起來(lái)。這留下給讀者做為一個(gè)練習(xí)。同樣程序能改變使用余 弦波做為基本函數(shù)工作-我們只需簡(jiǎn)單地改變 sin(arg)條件到 cos(arg)來(lái)獲得離散余弦變換的直接實(shí)現(xiàn)(DC T)。
現(xiàn)在,就象在這篇文章較前面的段落中我們討論過(guò)的那樣,我們?cè)趯?shí)踐中沒(méi)有辦法區(qū)分一個(gè)被測(cè)量的正 弦類函數(shù)象是正弦波還是余弦波。做為代替我們總是測(cè)量正弦信號(hào),且正弦和余弦變換在實(shí)踐中沒(méi)有太大 的用途,除了一些特殊情況(象圖象壓縮的地方,即毎塊圖象具有能用一個(gè)基本的余弦或正弦函數(shù)較好模 擬特性,例如能用余弦基本函數(shù)較好表現(xiàn)的相同顏色的大區(qū)域)。正弦信號(hào)是一個(gè)比正弦或余弦波更一般 的片斷,因?yàn)樗梢蚤_(kāi)始在在它的周期中的一個(gè)任意位置。我們記得,當(dāng)余弦波開(kāi)始于 1 時(shí),正弦波總開(kāi) 始在 0。當(dāng)我們采取正弦波作為參考,余弦波開(kāi)始在它的周期的最后 1/4 之處。一般用度或弧度測(cè)量它們 的偏移量,這是兩個(gè)一般與三角函數(shù)相關(guān)的單位。一個(gè)完整的周期等于 360°(代表 "度") 或 2π 個(gè)弧度(代表"2π" ,"π" 發(fā)音象“pie” 。π 是希臘字表示數(shù) 3.14159265358979323846... 在三角學(xué)方面有重要意義) 。
余弦波因而有一個(gè) 90°或 π/2 的偏移。這偏移叫正弦信號(hào)的相位,因此余弦波相對(duì)正弦信號(hào)有 90°或 π/2 相位。
相位的事情就有這些內(nèi)容。因?yàn)槲覀円恢辈荒芟薅ㄐ盘?hào)在 0°或 90°相位開(kāi)始(因?yàn)槲覀冋^測(cè)一個(gè)我們 可能無(wú)法控制的信號(hào)),它對(duì)同時(shí)直接唯一的描述信號(hào)的頻率、振幅、相位至關(guān)重要。以正弦或余弦做變換相位限制在 0°或 90°,一個(gè)具有任意相位的正弦信號(hào)將引起相鄰頻率出現(xiàn)假峰(因?yàn)樗鼈冊(cè)噲D“ 幫助” 分析,強(qiáng)制給被測(cè)信號(hào)加上一個(gè) 0°或 90°的相位作用)。它有些象用一圓石頭去填滿一個(gè)方孔:你需要小一 些的圓石頭去填充剩余的空間,并且更小的石頭填好依然留出空的空間,等等。我們所需要的是能處理一 般信號(hào)的變換,它能處理任意相位正弦波構(gòu)成的信號(hào)。
步驟 6:離散傅葉變換
從正弦變換到傅里葉變換的步驟是簡(jiǎn)單的,只需用更一般的方法。在正弦變換中對(duì)每個(gè)頻率上的測(cè)度 使用正弦波,在傅里葉變換中正弦、余弦波二者都使用。就是說(shuō),對(duì)任意的當(dāng)前頻率,我們以同一頻率的 正弦和余弦波來(lái)“ 比較” (或“ 共振” )被測(cè)信號(hào)。如果我們的信號(hào)看起來(lái)很象正弦波,變換的正弦部份將有 一個(gè)大的幅值。如果它看起來(lái)象余弦波,變換的余弦部份將有一個(gè)大的幅值。如果看起來(lái)象反相的正弦波, 也就是說(shuō),它開(kāi)始于 0 但下降至-1 取代上升至 1,它的正弦部份將有一個(gè)大的負(fù)幅值。這表明用+、- 符號(hào)和正弦、余弦相位能表示任意給定頻率的正弦信號(hào)[2]。
Listing 1.2: The direct realization of the Discrete Fourier Transform[3]:
#define M_PI 3.14159265358979323846
long bin, k;
double arg, sign = -1.; /* sign = -1 -> FFT, 1 -> iFFT */
for (bin = 0; bin <= transformLength/2; bin++) {
cosPart[bin] = (sinPart[bin] = 0.);
for (k = 0; k < transformLength; k++) {
arg = 2.*(float)bin*M_PI*(float)k/(float)transformLength;
sinPart[bin] += inputData[k] * sign * sin(arg);
cosPart[bin] += inputData[k] * cos(arg);
}
}
我們?nèi)赃z留著一個(gè)問(wèn)題,就是如何獲得傅里葉變換所缺乏的那些有用的東西。我說(shuō)過(guò)傳里葉變換的優(yōu)赿性超過(guò)正弦和余弦變換是因?yàn)橛谜倚盘?hào)工作。但至今我們還未看到任何正弦信號(hào),仍只有正弦和余弦。好,這需要一點(diǎn)附加處理步聚:
#define M_PI 3.14159265358979323846
long bin;
for (bin = 0; bin <= transformLength/2; bin++) {
/* frequency */
frequency[bin] = (float)bin * sampleRate / (float)transformLength;
/* magnitude */
magnitude[bin] = 20. * log10( 2. * sqrt(sinPart[bin]*sinPart[bin] + cosPart[bin]*c
osPart[bin]) / (float)transformLength);
/* phase */
phase[bin] = 180.*atan2(sinPart[bin], cosPart[bin]) / M_PI - 90.;
}
在運(yùn)行清單 1.3 所示的關(guān)于 DFT 輸出的代碼段之后,我們結(jié)束被看作以正弦信號(hào)波的和的輸入信號(hào)表示。
K 序正弦信號(hào)是用 frequency[k],magnitude[k]和 phase[k]來(lái)描述的。單位是 Hz(Hertz,周/秒),dB(Decibel),和°(Degree)。請(qǐng)注意在經(jīng)過(guò)清單 1.3 的后加工(處理)即把正弦和余弦函數(shù)部份轉(zhuǎn)換成一個(gè)單一的正弦信 號(hào)之后,我們命名 K 序正弦信號(hào)的振幅-DFT 存貯為幅度,且它總是取相對(duì)值。我們可以說(shuō)一個(gè)-1.0 的振 幅對(duì)應(yīng)于 1.0 的幅度,對(duì)應(yīng)于相位+或-180°。在文獻(xiàn)中,做做傅里葉變換的場(chǎng)合,隊(duì)列 magnitude[] 被稱 作被測(cè)信號(hào)的幅度譜,隊(duì)列 phase[]被稱作被測(cè)信號(hào)的相位譜。
如用分貝測(cè)量存貯幅度的參考,輸入波也期望有一個(gè)在[-1.0,1.0]之間的采樣值,相對(duì)于 0dB 幅度滿刻 度數(shù)字。做為一個(gè) DFT 的有趣應(yīng)用,比如清單 1.3 就可被用于寫一個(gè)基于離散傅里葉變換的譜分析。
結(jié)論
象我們已知那樣,傅里葉變換和其系列的離散正弦和余弦變換,提供了把一個(gè)信號(hào)分解成一束分波的 便利工具。結(jié)果有正弦或余弦之一,或正弦信號(hào)(用正弦和余弦波的組合來(lái)描述)。在傅里葉變換中同時(shí) 使用正弦和余弦波的好處是我們因而能引入相位的概念,它使變換更一般化,因而我們能用它有效清楚地 分析既不是純正弦也不是純余弦的正弦信號(hào),當(dāng)然其它信號(hào)也一樣。
傅里葉變換與被考察信號(hào)無(wú)關(guān),因而無(wú)論我們正分析的信號(hào)是一個(gè)正弦信號(hào)或是一些其它的更復(fù)雜的, 變換需要相同的操作數(shù)。這就是為什么傅里葉變換被稱做無(wú)參數(shù)變換的原因,這意味著它對(duì)需要的信號(hào)“ 智能的” 分析沒(méi)有直接的幫助(在考察一個(gè)我們已知是一個(gè)信號(hào)是正弦曲線的情況下,我們更喜歡精確地獲 得關(guān)于相位,頻率,幅度的信息以代替一串在一些預(yù)定頻率上的正弦和余弦波)。
現(xiàn)在我們也知道了我們是在求輸入信號(hào)在一組固定頻率柵格上的值,輸入信號(hào)實(shí)際存在的頻率組在這 組柵格上可能不起作用。我們?cè)诜治鲋欣玫臇鸥袷侨藶榈模驗(yàn)槲覀儙缀醢凑贞P(guān)于它們的頻率的嘗試來(lái) 選擇參考正弦、余弦波。說(shuō)到了這些,馬上清楚了一個(gè)將要很容易遇到的要點(diǎn),即被測(cè)信號(hào)的頻率位于變 換柵格的頻率之間。因此,有一個(gè)頻率發(fā)生在位于兩個(gè)頻率柵格之間的正弦曲線,在變換中將不好被描述。包圍著與輸入信號(hào)頻率最接近的柵格的相鄰的柵格將試圖‘改正’ 頻率的背離。因而,輸入信號(hào)的能量將拖 尾至數(shù)個(gè)相鄰的柵格。這也是傅里葉變換不能迅速地分析聲音返回它的基波和諧波(并且,這也是為什么 我們稱正弦和余弦波為分波而不諧波和泛音)。
簡(jiǎn)單的說(shuō),沒(méi)有進(jìn)一步的快速處理,DFT 和一個(gè)狹窄的壩一樣,細(xì)小并行的帶通濾波器組(“ 通道” )和每個(gè)通道帶有附加的相位信息。這對(duì)分析信號(hào)、做濾波器和運(yùn)用其它的技巧是有益的(改變一個(gè)信號(hào)的 音調(diào)而不改變它的速度是它們其中之一,說(shuō)明在 DSPdimension.com 上另一篇不同的文章中),但它需 要對(duì)少量普通任務(wù)附加快速處理。同樣,它能被認(rèn)為是使用除了正弦和余弦波基本函數(shù)的變換系列的一個(gè) 特例。在這個(gè)方向上展開(kāi)概念超出了這篇文章的范圍。
最后,重要的是要提及一個(gè)更高效的 DFT 工具,也就是一個(gè)被稱做快速傅里葉變換的算法。它最初 是由庫(kù)利和圖克在 1969 年構(gòu)思的(它的根源仍然要追溯到高斯和其它人的工作)。FFT 只是一個(gè)高效的 算法,它比上面給出的以直接逼近計(jì)算 DFT 所化的時(shí)間少,它是結(jié)果完全相同的其它方法。無(wú)論如何,F(xiàn) FT 是以庫(kù)利/圖克算法實(shí)施的,它需要變換長(zhǎng)度是 2 的冪。在實(shí)踐中,對(duì)大多數(shù)應(yīng)用來(lái)說(shuō)這是一個(gè)可以接 受的限制。有大量的以不同方法實(shí)施 FFT 的可利用的文獻(xiàn),因而,可以說(shuō)有足夠多不同的 FFT 實(shí)現(xiàn),其中一些并不需要經(jīng)典 FFT 的 2 的冪的限制。
下面清單 1.4 以程序 smbFft()給出了一個(gè) FFT 的實(shí)現(xiàn)。
Listing 1.4: The Discrete Fast Fourier Transform (FFT):
#define M_PI 3.14159265358979323846
void smbFft(float *fftBuffer, long fftFrameSize, long sign)
/*
FFT routine, (C)1996 S.M.Bernsee. Sign = -1 is FFT, 1 is iFFT (inverse)
Fills fftBuffer[0...2*fftFrameSize-1] with the Fourier transform of the time domain data in fftBuffer
[0...2*fftFrameSize-1]. The FFT array takes and returns the cosine and sine parts in an interleaved
manner, ie. fftBuffer[0] = cosPart[0], fftBuffer[1] = sinPart[0], asf. fftFrameSize must be a power of
2. It expects a complex input signal (see footnote 2), ie. when working with 'common' audio sig
nals
our input signal
has to be passed as {in[0],0.,in[1],0.,in[2],0.,...} asf. In that case, the transform
of
the frequencies of
interest is in fftBuffer[0...fftFrameSize].
*/
{
float wr, wi, arg, *p1, *p2, temp;
float tr, ti, ur, ui, ur, ui, *p1r, *p1i, *p2r, *p2i;
long i, bitm, j, le, le2, k;
for (i = 2; i < 2*fftFrameSize-2; i += 2) {
for (bitm = 2, j = 0; bitm < 2*fftFrameSize; bitm <<= 1) {
if (i & bitm) j++;
j <<= 1;
}
if (i < j) {
p1 = fftBuffer+i; p2 = fftBuffer+j;
temp = *p1; *(p1++) = *p2;
*(p2++) = temp; temp = *p1;
*p1 = *p2; *p2 = temp;
}
}
for (k = 0, le = 2; k < (long)(log(fftFrameSize)/log(2.)); k++) {
le <<= 1;
le2 = le>>1;
ur = 1.0;
ui = 0.0;
arg = M_PI / (le2>>1);
wr = cos(arg);
wi = sign*sin(arg);
for (j = 0; j < le2; j += 2) {
p1r = fftBuffer+j; p1i = p1r+1;
p2r = p1r+le2; p2i = p2r+1;
for (i = j; i < 2*fftFrameSize; i += le) {
tr = *p2r * ur - *p2i * ui;
ti = *p2r * ui + *p2i * ur;
*p2r = *p1r - tr; *p2i = *p1i - ti;
*p1r += tr; *p1i += ti;
p1r += le; p1i += le;
p2r += le; p2i += le;
}
tr = ur*wr - ui*wi;
ui = ur*wi + ui*wr;
ur = tr;
-
信號(hào)處理
+關(guān)注
關(guān)注
48文章
1029瀏覽量
103284 -
傅里葉變換
+關(guān)注
關(guān)注
6文章
441瀏覽量
42600
原文標(biāo)題:一文吃透傅里葉變換
文章出處:【微信號(hào):EngicoolArabic,微信公眾號(hào):電子工程技術(shù)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
如何實(shí)現(xiàn)傅立葉變換算法?
周期信號(hào)的傅立葉變換.ppt
DSP進(jìn)行浮點(diǎn)快速傅立葉變換剖析
簡(jiǎn)述FPGA的快速傅立葉變換
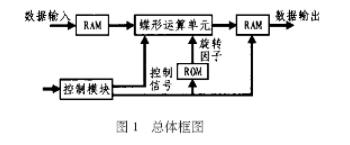




 傅立葉變換的實(shí)際應(yīng)用解析
傅立葉變換的實(shí)際應(yīng)用解析











評(píng)論