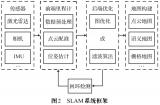
【導讀】SLAM是“Simultaneous Localization And Mapping”的縮寫,可譯為同步定位與建圖。最早,SLAM 主要用在機器人領域,是為了在沒有任何先驗知識的情況下,根據傳感器數據實時構建周圍環境地圖,同時根據這個地圖推測自身的定位。因此本文以簡單清晰的文字為大家介紹了視覺V-SLAM。
簡單的V-SLAM介紹,就當入門:)。
首先,從雙目立體幾何(stereo geometry)原理開始來定義外極(epipolar)約束:兩個攝像頭光心分別是 c0 和 c1,3-D 空間點 p 在兩個圖像平面的投影點分別是 x0 和 x1,那么直線 c0c1 和兩個圖像平面的交點即外極點(epipole)e0 和 e1,pc0c1 平面稱為外極平面(epipolar plane),它和兩個圖像平面的交線 l0 和 l1 即外極線(epipolar line);可以看到兩個攝像頭坐標系之間的轉換滿足(R,t),同時說明攝像頭 c0 的圖像點 x0 在攝像頭 c1 的圖像對應點 x1 一定落在其外極線 l1,反之依然;
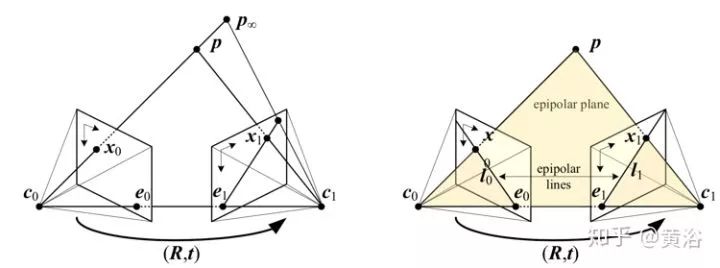
(a)對應一條光線的外極線 (b)對應的外極線集合和外極平面 外極線約束
這里需要定義一個本質矩陣(essential matrix)E 和一個基礎矩陣(fundamental matrix)F:E = [t]×R,其中 [t]× 是反對稱矩陣,即定義向量
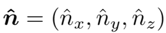
那么
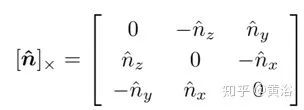
而 F = A?TEA?1,其中 A 是攝像頭內參數矩陣;對矩陣 E 和矩陣 F 來說,均滿足外極約束方程x1TEx0 =0,x1TFx0 =0
前者是攝像頭已標定情況下圖像特征點的對應關系,后者是攝像頭未標定情況下圖像特征點的對應關系;
其次,得到外極線約束(以F矩陣為例,E矩陣同樣)如下
l1=Fx0,l0=x1F,
以及,外極點約束(以F矩陣為例,E矩陣同樣)如下
Fe0=0,FTe1=0;
根據上面圖像特征點的外極約束方程,有8 點算法求解 F 和 E,以 F 為例,給定一組匹配特征點(n> 7)
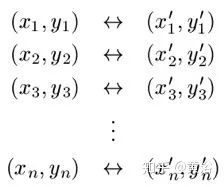
定義F矩陣元素fij(i=1~3,j=1~3),那么線性齊次方程組為
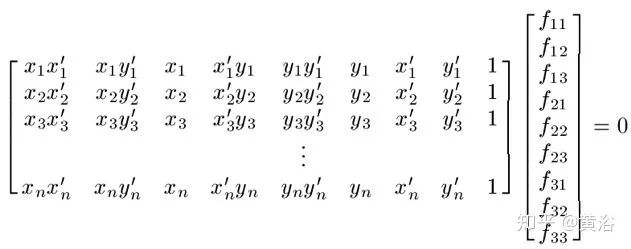
簡記為
Qf = 0
做SVD得到Q = USVT,而最終F的解是V最右的奇異向量(singular vector);
另外,因為E矩陣完全由攝像頭外參數(R和t共6個未知參數,但有一個不確定平移尺度量)決定,所以存在5 點算法求解E矩陣;
可以分解E得到攝像頭外參數,其步驟如下:
i. 同樣對E矩陣做奇異值分解(SVD):

ii. 那么第一個攝像頭投影矩陣簡單設為
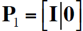
而第二個攝像頭矩陣P2有四種可能情況,如圖(a)-(d)所示:

其中
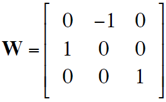
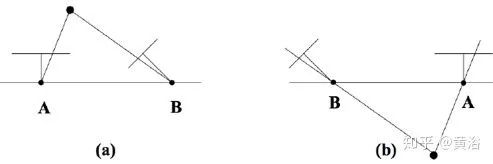
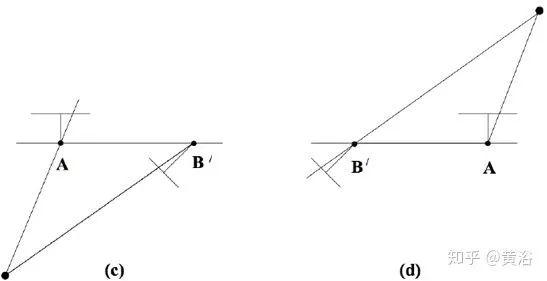
從E矩陣分解得到R和t
根據視圖方向與攝像頭中心到3-D點的方向之間夾角可以發現,四個可能中只有情況(a)是合理的解;
確定兩個視角的姿態之后,匹配的特征點 x,x’可以重建其 3-D 坐標X,即三角化(triangulation)理論;首先存在一個線性解:設兩個攝像頭投影矩陣為 P 和 P’,相應的它們列向量為pi,pi’,i=1~3,則有方程組:AX= 0
其中
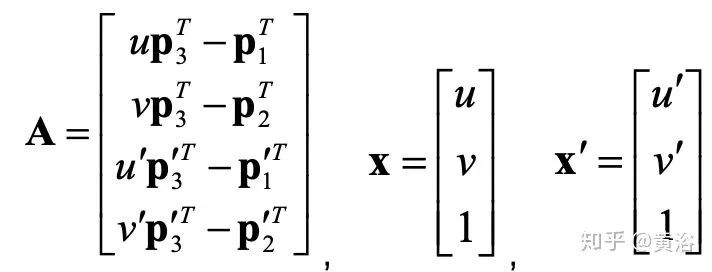
但一些誤差干擾的存在,上述線性解是不存在的;所以需要一個非線性的解,這里采用F 矩陣定義的外極約束方程xTFx’= 0,得到最小化誤差函數為
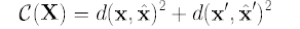
下面采用外極線 l, l’的來約束定義誤差,如圖所示,將目標函數重寫為

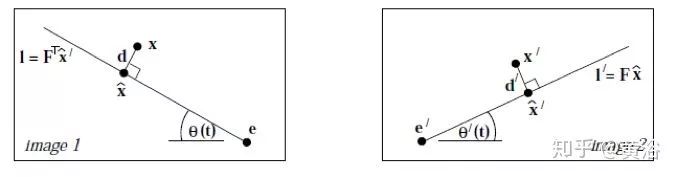
外極線定義的誤差
另外,在已知重建的 3-D 點集,如何和新視角的 2-D 圖像特征點匹配呢?這個問題解法稱為PnP(Perspective n Points),算法如下:
i. 首先,3D 點表示為 4 個控制點的加權和;
ii. 控制點坐標是求解的(12)未知數;
iii. 3D點投影到圖像上以控制點坐標建立線性方程;
iv. 控制點坐標表達為零特征向量(null eigenvectors)線性組合;
v. 上面組合的權重(bi)是新未知數(<4);
vi. 增加剛體(rigidity)約束以得到bi二次方程;
vii. 根據bi數目(無論線性化,或重新線性化)求解。
(注:有時候3-D-2-D匹配比3-D之間匹配的精度高)

PnP求解的示意圖
這里需要補充兩個概念,一是魯棒估計的隨機樣本共識法(RANSAC,RANdom SAmple Consensus),另一個是全局優化的集束修正法(BA,bundle adjustment):
i. RANSAC的目的是在包含異常點(outlier)的數據集上魯棒地擬合一個模型,如圖 2-12 所示:
1. 隨機選擇(最小)數據點子集并實例化(instantiate)模型;
2. 基于此模型,將所有數據點分類為內點(inlier)或異常點;
3. 迭代重復 1-2 步;
4. 選擇最大的內地集,以此重新估計最終模型。

RANSAC示意圖
ii. BA的目的是優化全局參數估計,對 SLAM 來說,結構重建的 3-D 點X和其對應的 2-D 特征點x,還有估計的視角變換參數(甚至包括攝像頭內參數)P,位于一個重投影(reprojection)誤差函數 D 最小化框架下(如圖所示),即

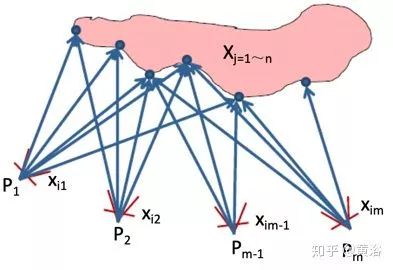
BA示意圖
這里集束(Bundle)指2-D點和3-D點之間的光線集,而修正(Adjustment)是指全局優化過程;其解法是非線性迭代的梯度下降法,如Gauss-Newton 方法和其修正 Levenberg-Marquardt 方法,因為問題自身的特性,這里的雅可比矩陣是非常稀疏的;另外,只取重建 3-D 點修正的話,稱為 structure only BA,而只取視角變換修正的話,稱為 motion-only BA;
在以上基礎之上,再重新審視SLAM過程:
i. 首先要提到概念 VO,即視覺里程計(visual odometry);VO 是 SLAM 的一部分,VO 主要是估計視角之間的變換,或者運動參數,它不需要輸出制圖(mapping)的結果,而且 BA 就是 motion-only 的模式;
ii. SLAM 方法分兩種途徑,一種是遞推濾波器方法,另一種是批處理估計方法;
a)濾波器方法,比如卡爾曼濾波遞推估計,實際上建立一個狀態空間的觀測模型和狀態轉換(運動)模型;觀察模型描述當攝像頭姿態和地標位置(來自于地圖)已知時觀測(地標)的概率; 運動模型是系統狀態(攝像頭姿態)轉換的概率分布,即馬爾可夫過程; 那么在遞歸貝葉斯估計中,同時更新系統狀態和建立的地圖,其中融合來自不同視角的觀測來完成制圖,而估計系統狀態可計算攝像頭的姿態,即定位問題;
b)批處理估計方法,也稱“關鍵幀”方法,其步驟是:
1)首先通過選擇的頭兩(關鍵)幀,采用雙目幾何的特征點匹配得到初始的3-D點云重建;
2)正常模式:假設 3D 地圖可用,并且估計出攝像頭增量運動,跟蹤特征點并使用 PnP 進行攝像頭姿態估計;
3)恢復模式:假設 3D 地圖可用,但跟蹤失敗故沒有增量運動,可相對于先前重建的地圖重新定位(re-localize)攝像頭姿勢;
4)關鍵幀 BA:保持一個“關鍵幀”子集,狀態向量是所有關鍵幀的 3D 地標和對應攝像頭姿勢,BA 可以在與跟蹤模塊并列的線程中調整狀態估計;
(注意:關鍵幀的選擇策略是算法性能很重要的一個因素)
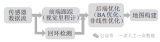
SLAM 中的閉環(loop closure)問題:當攝像頭又回到原來位置,稱為閉環,需要檢測閉環,并以此在 BA 框架下優化結構和運動估計;閉環檢測和重定位是類似的,可以基于圖像特征的匹配實現,俗稱“基于圖像的重定位(image-based re-localization),當關鍵幀子集較大的時候,需要對特征匹配進行壓縮和加速,比如詞包(bag of words)法和K維-樹(KD-tree)數據結構等等;
SLAM 中的傳感器可以是單目、雙目、深度傳感器(RGB-D)甚至激光雷達,也可以和 IMU 融合,稱為 VINS(visual inertial navigation system)。
附錄:G-N 和 L-M 的非線性最小二乘算法
假設有觀測向量 zi’,其預測模型為 zi = zi(x),其中x為模型參數;那么最小二乘(LS)法就是最小化如下代價函數:平方誤差加權和(weighted Sum of Squared Error,SSE)

其中 Wi 是一個任意對稱正定(symmetric positive definite,SPD) 矩陣,特征誤差函數為
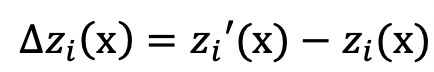
雅可比矩陣J和黑森(Hessian)矩陣H的計算為



那么 H 近似為
H≈J?WJ
作為梯度下降法,其 G-N 迭代的步進量即 z → z + delta z,由下面方程組計算
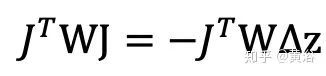
對于上面 G-N 的迭代步進量計算,可能左邊的矩陣不可逆。為此,一種改進的方法是在對角線元素中加入阻尼因子(Damped factor),即 L-M 迭代的步進量計算變成如下方程組
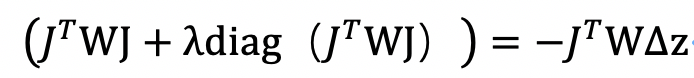
-
機器人
+關注
關注
211文章
28578瀏覽量
207795 -
攝像頭
+關注
關注
60文章
4857瀏覽量
96031 -
SLAM
+關注
關注
23文章
426瀏覽量
31886
原文標題:簡單明了,一文入門視覺SLAM
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種基于MASt3R的實時稠密SLAM系統
利用VLM和MLLMs實現SLAM語義增強


最新圖優化框架,全面提升SLAM定位精度

激光雷達在SLAM算法中的應用綜述
MG-SLAM:融合結構化線特征優化高斯SLAM算法

從算法角度看 SLAM(第 2 部分)

深度解析深度學習下的語義SLAM
工程實踐中VINS與ORB-SLAM的優劣分析

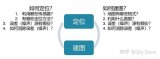
什么是SLAM?SLAM算法涉及的4要素
什么是SLAM?基于3D高斯輻射場的SLAM優勢分析
從基本原理到應用的SLAM技術深度解析




 簡單的V-SLAM介紹
簡單的V-SLAM介紹











評論