神經網絡的學習的目的是找到使損失函數的值盡可能小的參數。這是尋找最優參數的問題，解決這個問題的過程稱為最優化（optimization）。遺憾的是，神經網絡的最優化問題非常難。這是因為參數空間非常復雜，無法輕易找到最優解（無法使用那種通過解數學式一下子就求得最小值的方法）。而且，在 深度神經網絡中，參數的數量非常龐大，導致最優化問題更加復雜。

為了找到最優參數，我們將參數的梯度（導數）作為了線索。 使用參數的梯度，沿梯度方向更新參數，并重復這個步驟多次，從而逐漸靠近最優參數，這個過程稱為隨機梯度下降法（stochastic gradient descent），簡稱SGD。SGD是一個簡單的方法，不過比起胡亂地搜索參數空間，也算是“聰明”的方法。

打個比方： 有一個性情古怪的探險家。他在廣袤的干旱地帶旅行，堅持尋找幽 深的山谷。他的目標是要到達最深的谷底（他稱之為“至深之地”）。這 也是他旅行的目的。并且，他給自己制定了兩個嚴格的“規定”：一個 是不看地圖；另一個是把眼睛蒙上。因此，他并不知道最深的谷底在這個廣袤的大地的何處，而且什么也看不見。在這么嚴苛的條件下，這位 探險家如何前往“至深之地”呢？他要如何邁步，才能迅速找到“至深 之地”呢？

尋找最優參數時，我們所處的狀況和這位探險家一樣，是一個漆黑的世界。我們必須在沒有地圖、不能睜眼的情況下，在廣袤、復雜的地形中尋找 “至深之地”。大家可以想象這是一個多么難的問題。

在這么困難的狀況下，地面的坡度顯得尤為重要。探險家雖然看不到周 圍的情況，但是能夠知道當前所在位置的坡度（通過腳底感受地面的傾斜狀況）。 于是，朝著當前所在位置的坡度最大的方向前進，就是SGD的策略。勇敢的探險家心里可能想著只要重復這一策略，總有一天可以到達“至深之地”。

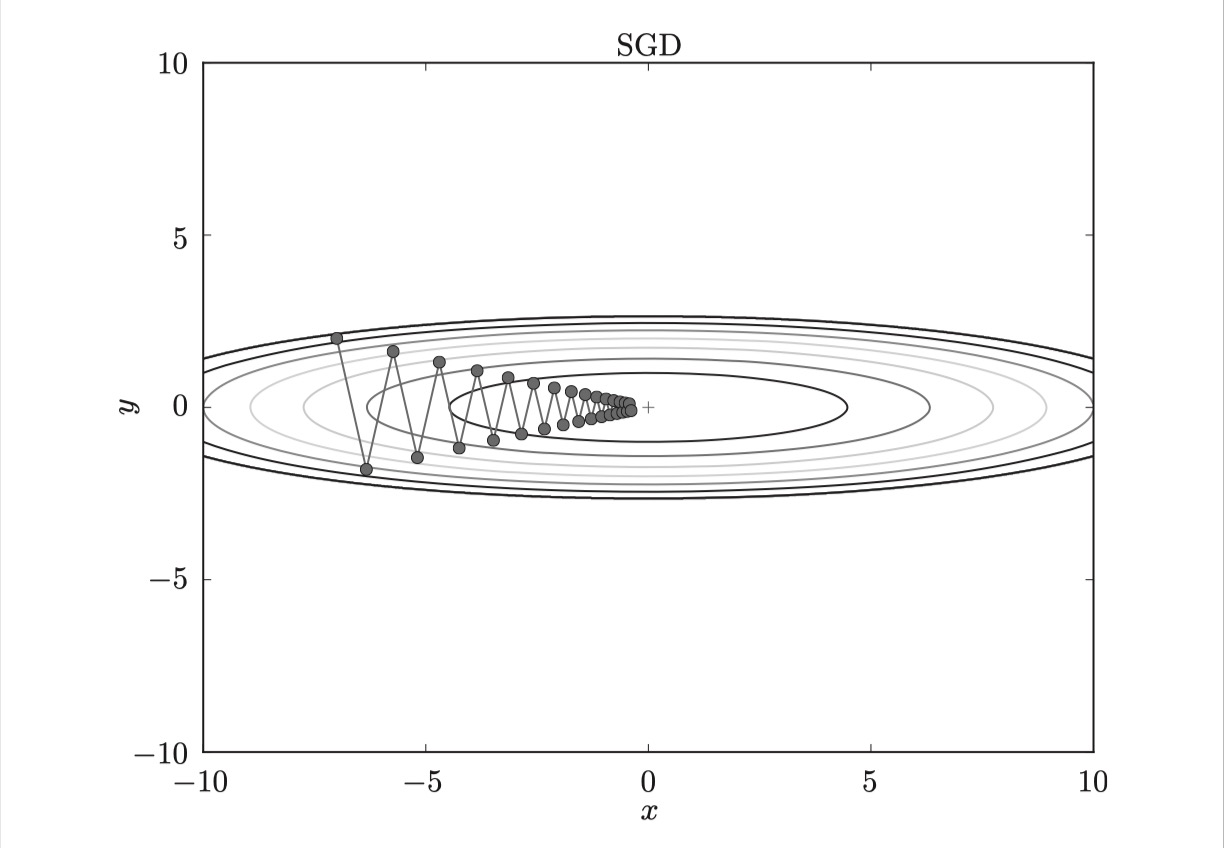
SGD

用數學式將SGD可以寫成如下形式：

為需要更新的權重參數，?L?W\frac{\partial L}{\partial W}?W?L為損失函數LLL關于WWW的梯度。η\etaη表示學習率，一般會取0.01或0.001這些事先決定好的值。式中的←\leftarrow←表示用右邊的值更新左邊的值。

缺點：

（1）SGD 因為更新比較頻繁，會造成 cost function 有嚴重的震蕩。

SGD呈 “之”字形移動。這是一個相當低效的路徑。也就是說， SGD的缺點是， 如果函數的形狀非均向（anisotropic），比如呈延伸狀，搜索的路徑就會非常低效。因此，我們需要比單純朝梯度方向前進的SGD更聰 明的方法。 SGD低效的根本原因是， 梯度的方向并沒有指向最小值的方向。

（2）容易收斂到局部最優，并且容易被困在鞍點。

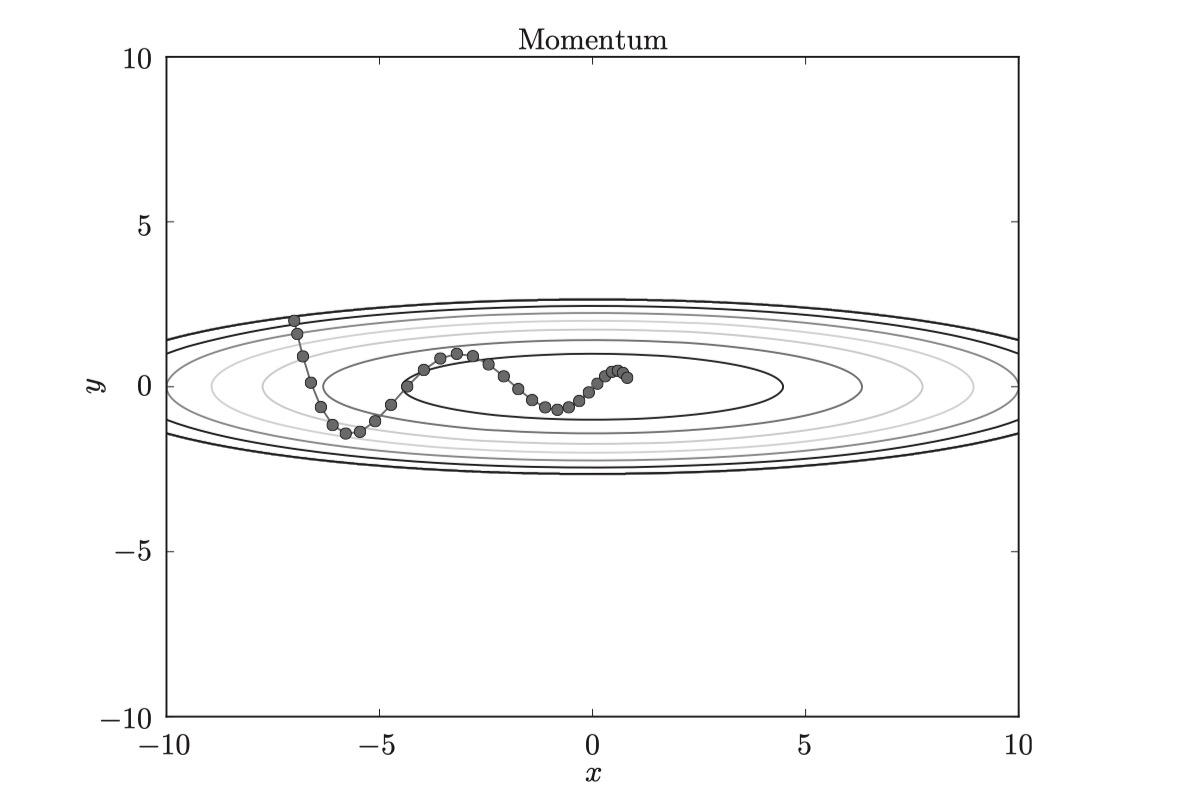
Momentum

Momentum算法借用了物理中的動量概念，它模擬的是物體運動時的慣性，即更新的時候在一定程度上保留之前更新的方向，同時利用當前batch的梯度微調最終的更新方向。這樣一來，可以在一定程度上增加穩定性，從而學習地更快，并且還有一定擺脫局部最優的能力：

和前面的SGD一樣， WWW表示要更新的權重參數， 表示損失函數關于WWW的梯度，ηηη表示學習率。 這里新出現了一個變量vvv，對應物理上的速度。 式（1）表示了物體在梯度方向上受力，在這個力的作用下，物體的速度增加這一物理法則。Momentum方法給人的感覺就像是小球在地面上滾動。

式（1）中有αvαvαv這一項。在物體不受任何力時，該項承擔使物體逐漸減速的任務（α設定為0.9之類的值），對應物理上的地面摩擦或空氣阻力。

和SGD相比， “之”字形的“程度”減輕了。這是因為雖然x軸方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一個方向會有一定的加速。反過來，雖然y軸方向上受到的力很大，但是因為交互地受到正方向和反方向的力，它們會互相抵消，所以y軸方向上的速度不穩定。因此，和SGD時的情形相比， 可以更快地朝x軸方向靠近，減弱“之”字形的變動程度。

AdaGrad

在神經網絡的學習中，學習率（數學式中記為ηηη）的值很重要。學習率過小， 會導致學習花費過多時間；反過來，學習率過大，則會導致學習發散而不能 正確進行。

在關于學習率的有效技巧中，有一種被稱為學習率衰減（learning rate decay） 的方法，即隨著學習的進行，使學習率逐漸減小。實際上，一開始“多” 學，然后逐漸“少”學的方法，在神經網絡的學習中經常被使用。

逐漸減小學習率的想法，相當于將“全體”參數的學習率值一起降低。 而AdaGrad進一步發展了這個想法，針對“一個一個”的參數，賦予其“定 制”的值。

AdaGrad會為參數的每個元素適當地調整學習率， 與此同時進行學習 （AdaGrad的Ada來自英文單詞Adaptive，即“適當的”的意思）。下面，讓我們用數學式表示AdaGrad的更新方法。

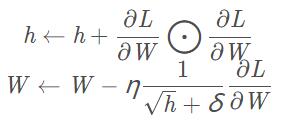
其中，hhh為梯度累積變量，它保存了以前的所有梯度值的平方和，hhh的初始值為0。?\bigodot?表示對應矩陣元素的乘法，η\etaη表示學習率，δ\deltaδ為很小的一個數值，是為了防止分母為0。然后，在更新參數時，通過乘以 1h√\frac{1}{\sqrt h}h1，就可以調整學習的尺度。這意味著， 參數的元素中變動較大（被大幅更新）的元素的學習率將變小。也就是說， 可以按參數的元素進行學習率衰減，使變動大的參數的學習率逐漸減小。

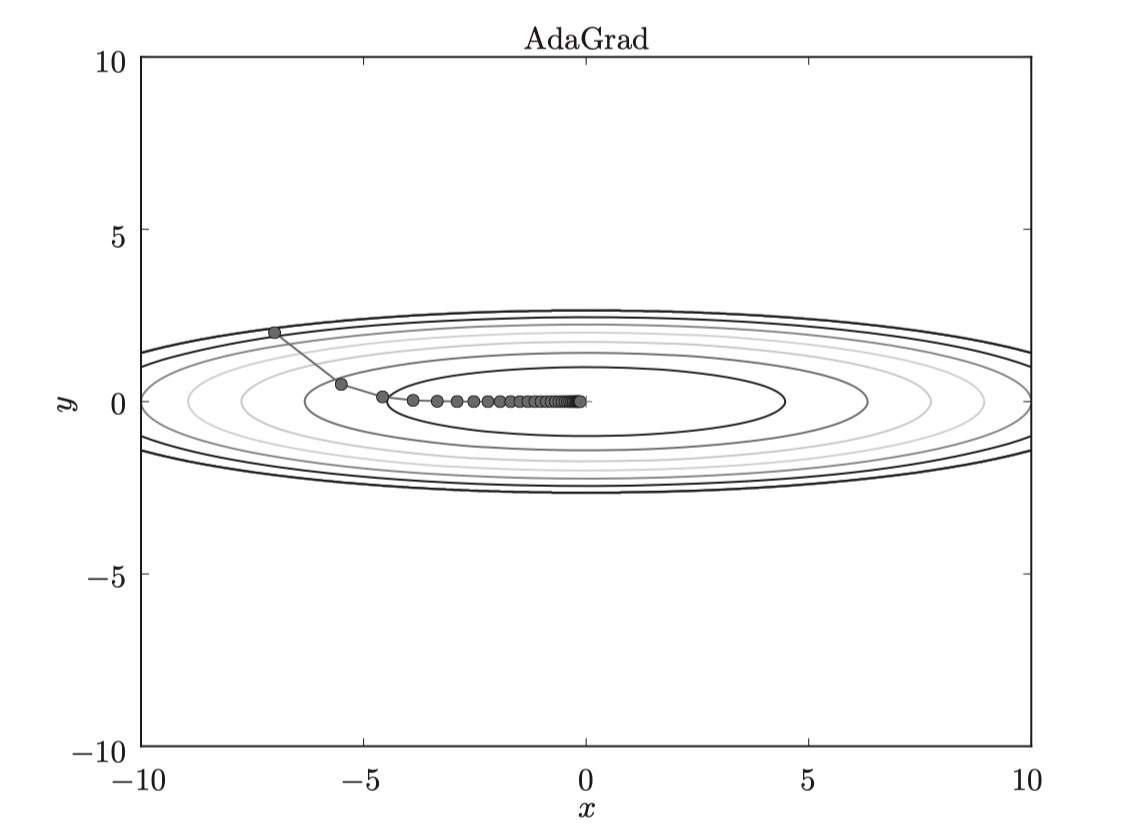
由圖可知，函數的取值高效地向著最小值移動。由于y軸方 向上的梯度較大，因此剛開始變動較大，但是后面會根據這個較大的變動按 比例進行調整，減小更新的步伐。因此，y軸方向上的更新程度被減弱，“之” 字形的變動程度有所衰減。

RMSProp

AdaGrad會記錄過去所有梯度的平方和。因此，學習越深入，更新 的幅度就越小。實際上，如果無止境地學習，更新量就會變為 0， 完全不再更新。為了改善這個問題，可以使用 RMSProp 方法。RMSProp方法并不是將過去所有的梯度一視同仁地相加，而是逐漸 地遺忘過去的梯度，在做加法運算時將新梯度的信息更多地反映出來。 這種操作從專業上講，稱為“指數移動平均”，呈指數函數式地減小過去的梯度的尺度。

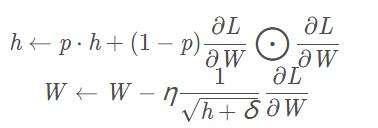
其中ppp一般可取0.9，其它參數和AdaGrad一致。

Adam

Momentum參照小球在碗中滾動的物理規則進行移動，AdaGrad為參數的每個元素適當地調整更新步伐。如果將這兩個方法融合在一起會怎么樣呢？這就是Adam方法的基本思路。直觀地講，Adam就是融合了Momentum和AdaGrad的方法。通過組合前面兩個方法的優點，有望實現參數空間的高效搜索。此外，進行超參數的“偏置校正”也是Adam的特征。Adam結合了Adagrad善于處理稀疏梯度和RMSprop善于處理非平穩目標的優點。

可以看出，直接對梯度的矩估計對內存沒有額外的要求，而且可以根據梯度進行動態調整，而?m?tn?t√+δ-\frac{\hat m_t}{\sqrt {\hat n_t} + \delta }?n^t+δm^t對學習率η\etaη形成了一個動態約束，而且有明確的范圍。

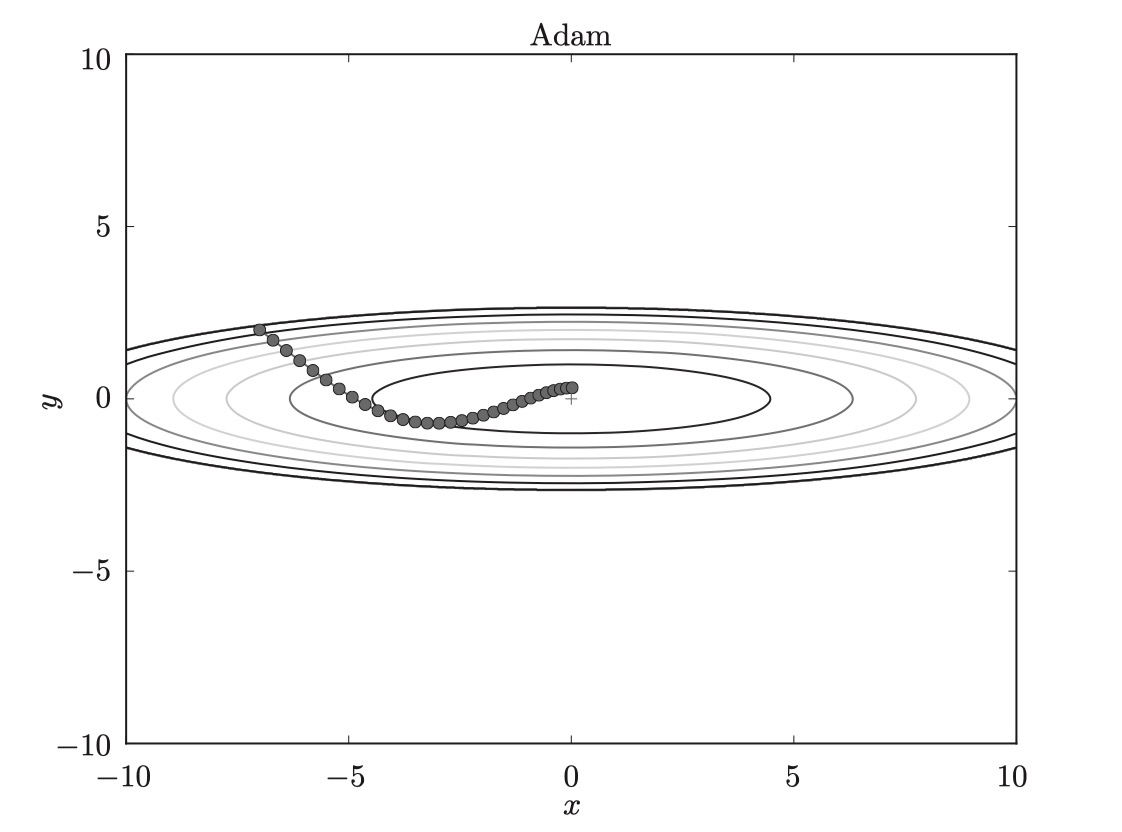
如圖，基于 Adam 的更新過程就像小球在碗中滾動一樣。雖然 Momentun 也有類似的移動，但是相比之下， Adam的小球左右搖晃的程度有所減輕。這得益于學習的更新程度被適當地調整了。