1、 S型曲線
1.1 簡介
Sigmoid函數是一個在生物學中常見的S型函數,也稱為S型生長曲線。Sigmoid函數也叫Logistic函數,取值范圍為(0,1),它可以將一個實數映射到(0,1)的區間,可以用來做二分類。該S型函數有以下優缺點:優點是平滑,而缺點則是計算量大。
Sigmoid函數由下列公式定義:
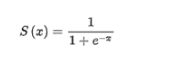
Sigmoid函數在[-8,8]的計算數值以及圖形如下:
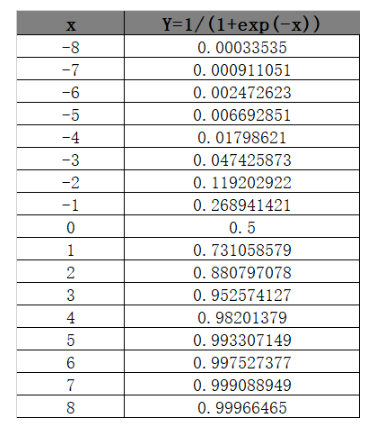
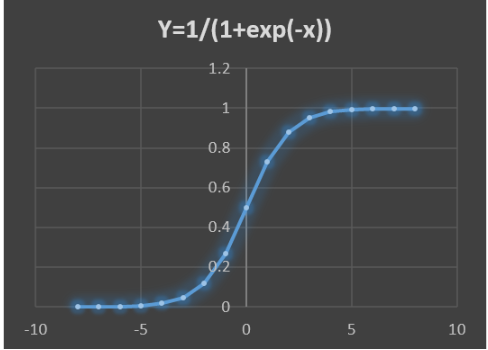
由以上數據與圖形可見,S型曲線就是指圖形中變化階段的曲線呈現一個英文字母'S'型,該曲線無限趨向于0和1,即取值范圍為(0,1)。
1.2 曲線延伸
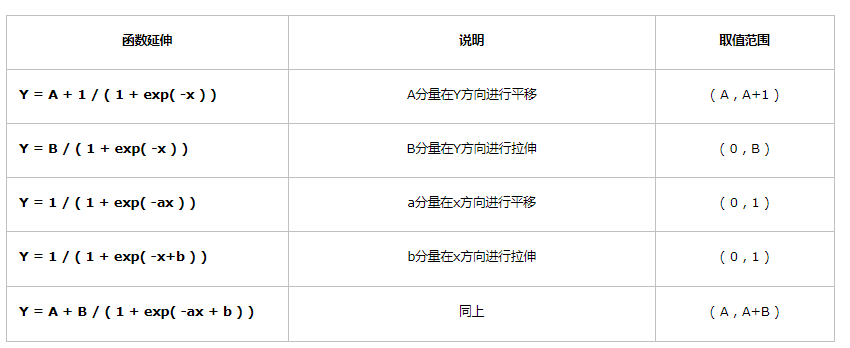
為了更直觀地觀察A、B、a、b分量對函數的影響,我整理 了一下對應的曲線圖,如下所示:
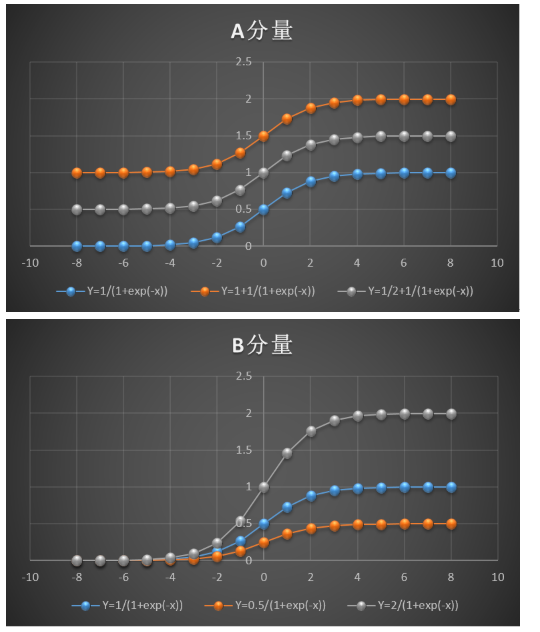
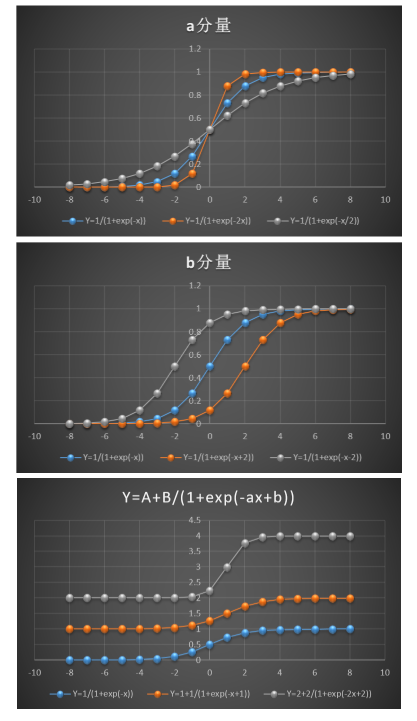
由圖可見,A、B分量影響的是曲線的取值范圍,而a、b分量影響的則是曲線的平滑程度。
2、應用場景 – 電機加減速控制
2.1 簡介
電機加減速,顧名思義,即電機以加速方式啟動,速度達到預設目標速度后保持一段時間勻速轉動,隨后又開始以減速方式轉動直至電機以一個較低的速度停止轉動。
一方面,電機加減速可以避免電機急開急停,進而可能對電機造成一定損壞;另一方面,也可以防止電機在高驅動速度不能起步的情況,即高驅動速度會出現空轉、丟步現象。因而,在電機需要達到一個較高的速度時,通常需要采用慢速加速驅動的方法,簡而言之,就是需要有一個加速過程。
例如:步進電機驅動負載可以按目標速度起動,若目標速度超過自身起動脈沖頻率時,則該情況下不能起動。因而,只有當起動頻率比電機起動脈沖頻率低時才能正常起動,采取加速的方式使速度線性地增加到目標速度,這種方法則稱為慢速加速驅動。
2.2 T型與S型
目前,在電機加減速控制上,普遍的加減速方法主要有T型加減速和S型加減速,實現方法則有公式法或查表法。
S型加減速相對于T型加減速更加平穩,對電機和傳動系統的沖擊更小,即S型加減速的優點是啟動和停止都很平滑,不會有很大的沖擊,但是也并非不存在缺點,缺點就是啟動和停止的時間比較長。
2.3 電機加減速控制
如要將S型曲線應用到電機的加減速控制上,需要將方程在X、Y坐標系進行平移,同時對曲線進行拉升變化:即 Y = A + B / ( 1 + exp( -ax + b ) ) ,則根據該曲線方程的相關特征可知,A、B分量可用于控制電機速度(頻率)的取值范圍,而a、b分量可用于控制速度(頻率)變化率。最終根據實際的需要,在加減速過程中采用以下的曲線方程為:
Fcurrent = Fstart + (Fend-Fstart)/(1+exp( -Flexible(i - Num )/ Num) )
= Fstart + (Fend-Fstart)/(1+exp( -(Flexible/Num)*i + Flexible) )
即此處相當于 A = Fstart 、B = Fend-Fstart 、a = Flexible/Num 、b = Flexible ,取值范圍為(Fstart,Fend),即加減速的起始速度(頻率)以及目標速度(頻率)。上述公式各變量說明如下:
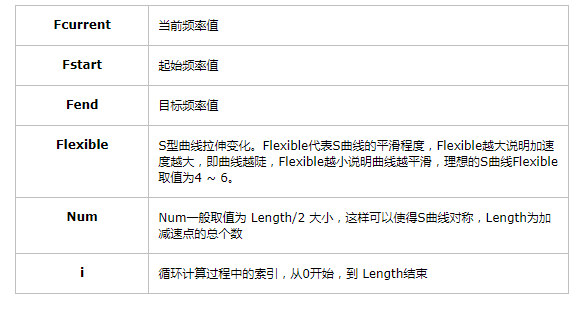
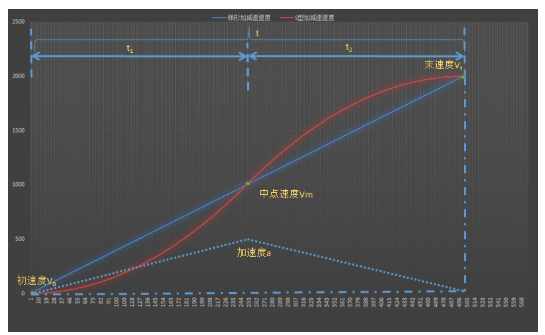
以上公式既可當作加速曲線,也可當作減速曲線。因此,一般情況下,我們只需要計算加速曲線,在減速時作反向操作即可。電機從10kHz加速到100kHz的加速曲線以及從100kHz減速到10kHz的減速曲線示例如下所示:
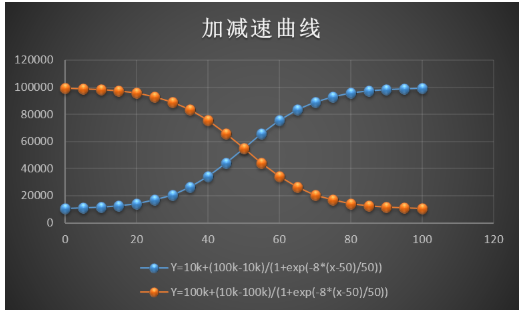
2.4 示例代碼
在電機加減速控制上,電機頻率越大,電機速度越快。因而,可以通過公式法求出每個加減速點的頻率值,進而通過電機頻率求出具體的脈沖周期,最后在間隔相同的時間內改變脈沖相關參數(分頻、周期、占空比)即可達到加減速的效果。一般情況下,如步進電機、伺服電機等,分頻與占空比通常固定數值即可,這樣在加減速過程僅需改變輸出周期值即可。同時,不同頻率脈沖輸出時也需要注意脈沖的連續性(即我們需要在當前脈沖完全輸出之后才能改變電機頻率),否則電機加減速過程就會出現丟步現象,在脈沖數嚴格要求的情況下造成累積誤差。
-
電機控制
+關注
關注
3537文章
1886瀏覽量
269013 -
傳動系統
+關注
關注
2文章
138瀏覽量
14487 -
加減速控制
+關注
關注
2文章
30瀏覽量
4017
發布評論請先 登錄
相關推薦
TMC9660智能伺服電機驅動控制芯片中文手冊
減速電機該如何分類?
伺服電機加減速機慣量怎么計算
stm32控制步進電機加減速的穩定性?
如何用stm32f103zet6控制伺服電機的加減速運動?
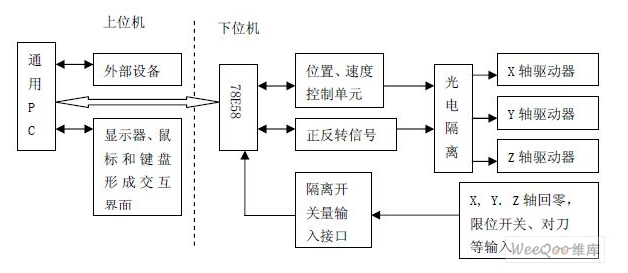
解析四次位移曲線的CNC數控系統的研究




 一文詳解電機S曲線加減速控制
一文詳解電機S曲線加減速控制














評論