logistic回歸是一種廣義的線性回歸,通過構造回歸函數(shù),利用機器學習來實現(xiàn)分類或者預測。
原理
上一文簡單介紹了線性回歸,與邏輯回歸的原理是類似的。
預測函數(shù)(h)。該函數(shù)就是分類函數(shù),用來預測輸入數(shù)據的判斷結果。過程非常關鍵,需要預測函數(shù)的“大概形式”, 比如是線性還是非線性的。 本文參考機器學習實戰(zhàn)的相應部分,看一下數(shù)據集。
// 兩個特征
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
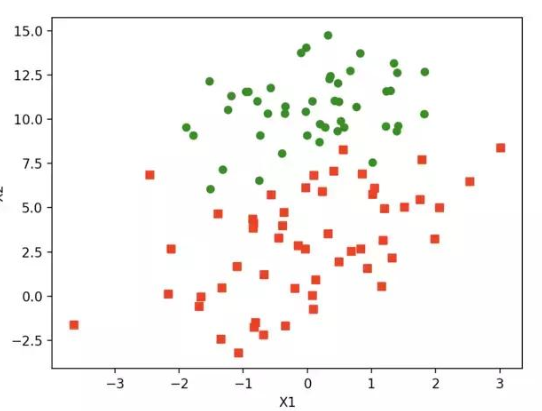
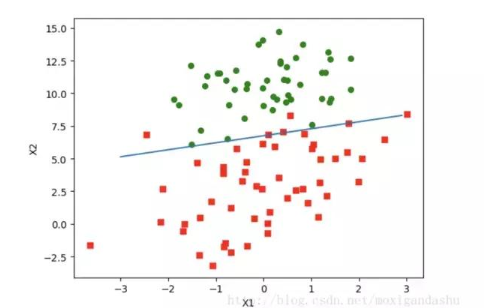
如上圖,紅綠代表兩種不同的分類。可以預測分類函數(shù)大概是一條直線。Cost函數(shù)(損失函數(shù)):該函數(shù)預測的輸出h和訓練數(shù)據類別y之間的偏差,(h-y)或者其他形式。綜合考慮所有訓練數(shù)據的cost, 將其求和或者求平均,極為J函數(shù), 表示所有訓練數(shù)據預測值和實際值的偏差。
顯然,J函數(shù)的值越小,表示預測的函數(shù)越準確(即h函數(shù)越準確),因此需要找到J函數(shù)的最小值。有時需要用到梯度下降。
具體過程
構造預測函數(shù)
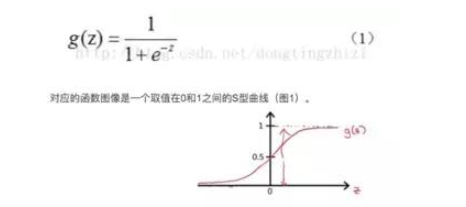
邏輯回歸名為回歸,實際為分類,用于兩分類問題。 這里直接給出sigmoid函數(shù)。
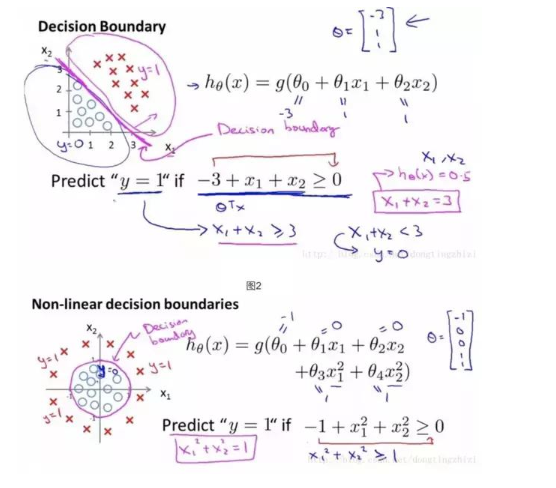
接下來確定分類的邊界,上面有提到,該數(shù)據集需要一個線性的邊界。 不同數(shù)據需要不同的邊界。
確定了分類函數(shù),將其輸入記做z ,那么
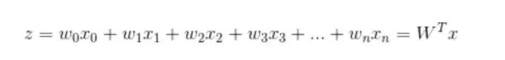
向量x是特征變量, 是輸入數(shù)據。此數(shù)據有兩個特征,可以表示為z = w0x0 + w1x1 + w2x2。w0是常數(shù)項,需要構造x0等于1(見后面代碼)。 向量W是回歸系數(shù)特征,T表示為列向量。 之后就是確定最佳回歸系數(shù)w(w0, w1, w2)。cost函數(shù)
綜合以上,預測函數(shù)為:
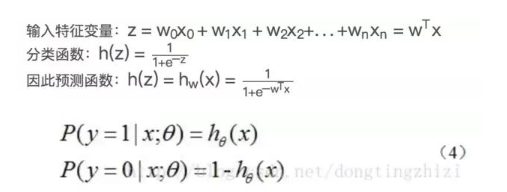
這里不做推導,可以參考文章 Logistic回歸總結
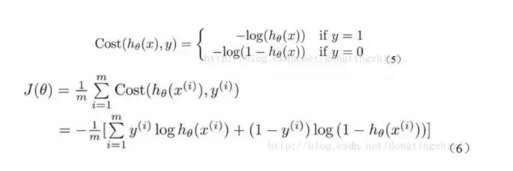
有了上述的cost函數(shù),可以使用梯度上升法求函數(shù)J的最小值。推導見上述鏈接。
綜上:梯度更新公式如下:

接下來是python代碼實現(xiàn):
# sigmoid函數(shù)和初始化數(shù)據
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def init_data():
data = np.loadtxt(‘data.csv’)
dataMatIn = data[:, 0:-1]
classLabels = data[:, -1]
dataMatIn = np.insert(dataMatIn, 0, 1, axis=1) #特征數(shù)據集,添加1是構造常數(shù)項x0
return dataMatIn, classLabels
復制代碼
// 梯度上升
def grad_descent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #(m,n)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
weights = np.ones((n, 1)) #初始化回歸系數(shù)(n, 1)
alpha = 0.001 #步長
maxCycle = 500 #最大循環(huán)次數(shù)
for i in range(maxCycle):
h = sigmoid(dataMatrix * weights) #sigmoid 函數(shù)
weights = weights + alpha * dataMatrix.transpose() * (labelMat - h) #梯度
return weights
// 計算結果
if __name__ == ‘__main__’:
dataMatIn, classLabels = init_data()
r = grad_descent(dataMatIn, classLabels)
print(r)
輸入如下:
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
上述w就是所求的回歸系數(shù)。w0 = 4.12414349, w1 = 0.4800, w2=-0.6168 之前預測的直線方程0 = w0x0 + w1x1 + w2x2, 帶入回歸系數(shù),可以確定邊界。 x2 = (-w0 - w1*x1) / w2
畫出函數(shù)圖像:
def plotBestFIt(weights):
dataMatIn, classLabels = init_data()
n = np.shape(dataMatIn)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if classLabels[i] == 1:
xcord1.append(dataMatIn[i][1])
ycord1.append(dataMatIn[i][2])
else:
xcord2.append(dataMatIn[i][1])
ycord2.append(dataMatIn[i][2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1,s=30, c=‘red’, marker=‘s’)
ax.scatter(xcord2, ycord2, s=30, c=‘green’)
x = np.arange(-3, 3, 0.1)
y = (-weights[0, 0] - weights[1, 0] * x) / weights[2, 0] #matix
ax.plot(x, y)
plt.xlabel(‘X1’)
plt.ylabel(‘X2’)
plt.show()
如下:
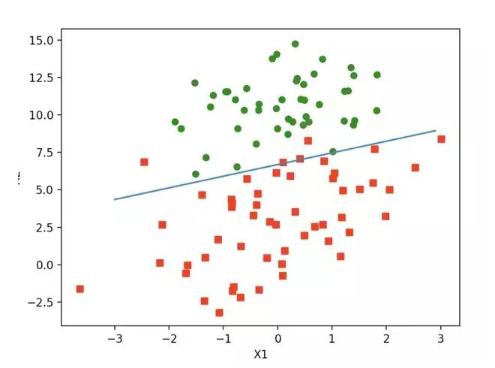
算法改進
隨機梯度上升
上述算法中,每次循環(huán)矩陣都會進行m * n次乘法計算,時間復雜度是maxCycles* m * n。當數(shù)據量很大時, 時間復雜度是很大。 這里嘗試使用隨機梯度上升法來進行改進。 隨機梯度上升法的思想是,每次只使用一個數(shù)據樣本點來更新回歸系數(shù)。這樣就大大減小計算開銷。 算法如下:
def stoc_grad_ascent(dataMatIn, classLabels):
m, n = np.shape(dataMatIn)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
h = sigmoid(sum(dataMatIn[i] * weights)) #數(shù)值計算
error = classLabels[i] - h
weights = weights + alpha * error * dataMatIn[i]
return weights
進行測試:
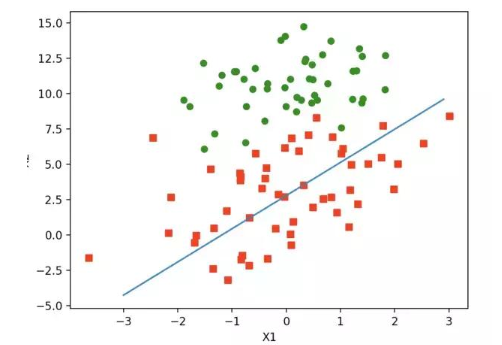
隨機梯度上升的改進
def stoc_grad_ascent_one(dataMatIn, classLabels, numIter=150):
m, n = np.shape(dataMatIn)
weights = np.ones(n)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 / (1 + i + j) + 0.01 #保證多次迭代后新數(shù)據仍然有影響力
randIndex = int(np.random.uniform(0, len(dataIndex)))
h = sigmoid(sum(dataMatIn[i] * weights)) # 數(shù)值計算
error = classLabels[i] - h
weights = weights + alpha * error * dataMatIn[i]
del(dataIndex[randIndex])
return weights
可以對上述三種情況的回歸系數(shù)做個波動圖。 可以發(fā)現(xiàn)第三種方法收斂更快。 評價算法優(yōu)劣勢看它是或否收斂,是否達到穩(wěn)定值,收斂越快,算法越優(yōu)。
總結
這里用到的梯度上升和梯度下降是一樣的,都是求函數(shù)的最值, 符號需要變一下。 梯度意味著分別沿著x, y的方向移動一段距離。(cost分別對x, y)的導數(shù)。
完整代碼請查看: github: logistic regression
參考文章: 機器學習之Logistic回歸與Python實現(xiàn)
-
機器學習
+關注
關注
66文章
8434瀏覽量
132871 -
Logistic
+關注
關注
0文章
11瀏覽量
8858 -
線性回歸
+關注
關注
0文章
41瀏覽量
4314
發(fā)布評論請先 登錄
相關推薦
傳統(tǒng)機器學習方法和應用指導

如何選擇云原生機器學習平臺
LuatOS開發(fā)之4G模組隨機數(shù)(random)|實戰(zhàn)指南

什么是機器學習?通過機器學習方法能解決哪些問題?

NPU與機器學習算法的關系
什么是回歸測試_回歸測試的測試策略
【「時間序列與機器學習」閱讀體驗】時間序列的信息提取
【「時間序列與機器學習」閱讀體驗】+ 鳥瞰這本書
【「時間序列與機器學習」閱讀體驗】+ 簡單建議
不同類型神經網絡在回歸任務中的應用
機器學習算法原理詳解
深度學習與傳統(tǒng)機器學習的對比
機器學習的經典算法與應用

機器學習8大調參技巧





 機器學習實戰(zhàn)之logistic回歸
機器學習實戰(zhàn)之logistic回歸










評論