零狀態響應就是電路在零初始狀態下(動態元件初始儲能為零)由外施激勵引起的響應。
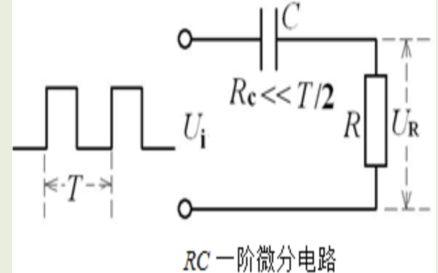
RC電路的零狀態響應
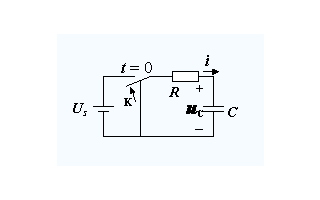
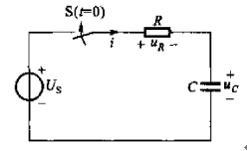
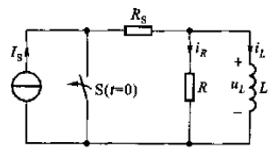
在t=0時刻,開關S閉合,電路接入直流電壓源US。根據KVL,有
uR+uC=US
(KVL∑u=0
指定回路的繞行方向是順時針的,R、C的電壓參考方向與繞行方向一致,電壓前面取“+”號,US的電壓參考方向與繞行方向不一致,前面取“-”號。
根據KVL,有
uR+uC-US=0
得
US=uR+uC)
將uR=Ri,i=CduC/dt代入,得電路的微分方程
RC(duC/dt)+uC=US
此方程為一階線性非齊次方程。方程的解由非齊次方程的特解uC'
和對應的齊次方程的通解uC''兩個分量組成,即
uC=uC'+uC''
不難求得特解為
uC'=US
(對于一階線性微分方程dy/dx+P(x)y=Q(x)
非齊次線性方程的通解
y=e-∫P(x)dx(∫Q(x)e∫P(x)dxdx+C)
取C=0便得到特解
y=e-∫P(x)dx∫Q(x)e∫P(x)dxdx
對于RC(duC/dt)+uC=US,uC=e-(t/RC)*** 但是對于求解這個實際問題不需要這樣循規蹈矩
最后電路穩定后,C相當于開路,那C兩端電壓就等于電壓源兩端電壓,所以特解是現成的,即uC'=US)
而齊次方程RCduC/dt+uC=0的通解為
uC''=Ae-t/τ
其中τ=RC。因此
uC=US+Ae-t/τ
代入初始值,可求得
A=-US
而
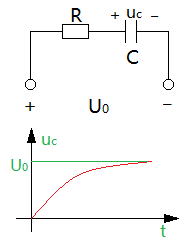
uC=US-USe-t/τ=US(1-e-t/τ)
i=C(duC/dt)=(US/R)e-t/τ
WR=(1/2)CUS2(充電效率只有50%)
編輯:hfy
-
RC電路
+關注
關注
2文章
162瀏覽量
30257
發布評論請先 登錄
相關推薦




 淺談RC電路的零狀態響應
淺談RC電路的零狀態響應
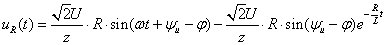










評論