前一段時間，推文中介紹了兩款參賽同學根據(jù)負反饋原理制作的恒磁20kHz的信號源，有效的解決了智能車比賽場地中電磁導線的長度，直徑等引起的電磁線圈的阻抗變化，從而對于輸出信號中20kHz基波信號帶來影響，提高了比賽場地導引信號的精度。

兩款信號源中，都采用了10mH電感和6.8nF電容組成的諧振選頻回路，對輸出電流信號中20kHz基波信號進行檢測。通過負反饋的原理來穩(wěn)定輸出電流信號中基波的幅值。

是否還可以采用別的方法來檢測輸出電流信號的基波呢？下面給大家所介紹，就是通過普通的電阻對輸出電流進行采樣，通過軟件算法來獲取輸出電流的基波分量。

實驗仍然采用傳統(tǒng)的數(shù)字信號源，輸出所使用的20kHz，100mA的方波交流信號。在信號輸出線中串入一個0.1歐姆的電阻，將電流信號轉變成電壓信號。

為了便于單片機采集該信號。使用了INA199對于電阻兩端的電壓進行差模放大，放大倍數(shù)50倍。由于IN199的帶寬只有14kHz，它對于電流信號中的高頻信號 有著較大的衰減。下圖中，可以看到在采樣電阻兩端的電壓信號經過INA199差模放大之后，信號的上升沿和下降沿變得光滑了。信號失真是由于它中間的高頻分量被衰減了。

雖然信號出現(xiàn)了失真，但這只是低通濾波器將其中的高頻信號濾除了。對于20kHz基波信號衰減不大。并且這是一個線性低通濾波器，所以對于后面的測量校正不會帶來很大的影響。

使用單片機軟件算法來獲取電流信號的基波頻率分量，首先需要通過ADC（模擬數(shù)字轉化器）對于輸入信號進行采樣，然后再進行頻率分析。由于單片機的ADC性能和計算能力有限，所以需要使用信號欠采樣和快速傅里葉變換計數(shù)。下面分別進行介紹。

信號欠采樣

根據(jù)信號采樣香儂(Claude Shannon)定理，如果信號采樣頻率大于信號中最高頻率的兩倍，則信號可以無損失進行恢復，否則就會造成信息的丟失和頻率混疊。通常稱信號最高頻率的兩倍為信號的奈奎斯特（Nyquist）采樣頻率。在實際應用中情況下，需要采樣頻率大于信號最高頻率的五倍以上。

對于方波電流信號，理論上，它的最高頻率是無窮大。這樣就會給信號采樣帶來很大的麻煩。如果采樣頻率無法滿足奈奎斯特頻率，就會產生信號的頻率混疊現(xiàn)象，表現(xiàn)在原本信號中高頻分量在采集后所形成的序列反而是低頻序列。這樣就會造成信號頻率分量出現(xiàn)偏差。

20kHz的電流信號，具有豐富的高次諧波。如果考慮到信號的10次諧波作為信號的最高頻率。那么所需要的采樣頻率就是20000102=400,000Hz。這個頻率對于普通的單片機來說已經到來它的上限了。如下是設置單片機ADC不同的轉換時間，所采集到的電流信號。

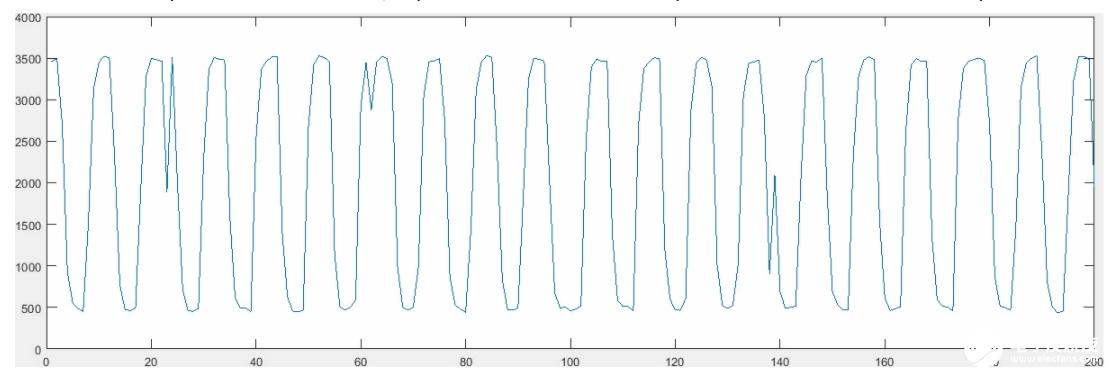
可以看出，在轉換時間小的情況下，是可以采集到比較完整的電流波形，但是，數(shù)據(jù)中會帶有很大的噪聲。如果轉換時間設置長了，就會出現(xiàn)明顯的欠采樣的情況，數(shù)據(jù)波形與實際信號波形之間出現(xiàn)了很大的差別。

如何解決這個矛盾了。這里需要應用到電流信號是周期信號的特點，可以使用信號欠采樣來獲得信號完整的波形。

欠采樣是巧妙應用到頻譜混疊，將原本高頻的諧波，變成低頻的諧波，從而可以在遠小于信號的奈奎斯特采樣頻率下完成信號的采集。

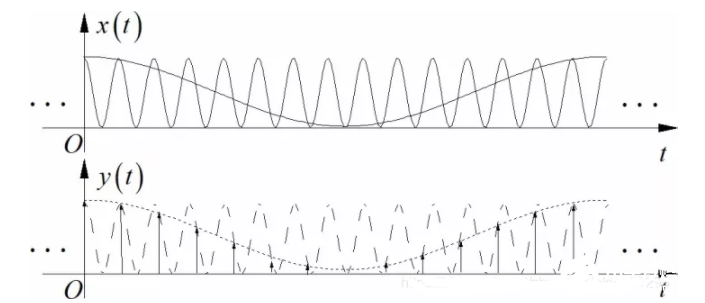
從時域分析來看，采樣的周期比信號的周期（或者信號周期的整數(shù)倍數(shù)）略大，比如大了deltaT，它遠遠小于信號的周期T。這樣每一個周期只采集一個數(shù)據(jù)，下一個周期的的采樣點會往后延遲deltaT.。將若干個周期中不同位置的采樣數(shù)據(jù)拼合在一起就可以形成信號的完整周期的數(shù)據(jù)。下圖就可以看出，一個高頻正弦波，在欠采樣下，可以形成一個低頻的正弦序列波形。

對于20kHz的信號，它的一個周期為50微妙。下圖是采用周期是50.172微秒的間隔對電流信號進行采集所獲得數(shù)據(jù)波形，可以看出它是原來電流波形的完美體現(xiàn)。

通過MATLAB中的FFT命令，可以求解出數(shù)據(jù)中的各個頻率分量幅度（成為幅度譜）。具體結果如下圖所示。

頻譜顯示，上述波形中，它的基波以及各個奇次（3,5,7…）諧波都存在，并隨著頻率的增加而減小。所有的偶次（2,4,6…）諧波都不存在。這是由于原始的對稱方波屬于奇諧信號，這樣的信號以及它的線性變換都不存在偶次諧波。相關的介紹在“分數(shù)諧波”推文中介紹過。

FFT

獲取信號中的各個諧波分量的幅值，可以通過傅里葉變換求得。對于采集所得到的離散序列來講，所使用變換就是離散傅里葉變換（DFT）。在上個世紀60年代，出現(xiàn)的離散傅里葉變換的快速算法（FFT）使得DFT的計算復雜度從O(N^2)降低到N*log2(N)，這使得頻譜分析快速進入了實際工程應用中。

問題是，快速傅里葉變換是否是最快，最有效的分析方法呢？

這需要看應用的具體需求。在有些情況下，反而直接應用DFT所需要的計算量比FFT還要小。比如在這里，由于我們只需要求出信號中20kHz的基波信號分量，即信號頻譜中對應20kHz的系數(shù)X[k]，所以直接使用上述DFT公式計算X[k]則只需要N次復數(shù)乘法和N-1次復數(shù)加法即可。反而比Log2(N)*N次的FFT更少。

由于計算需要使用到Exp(2pijkn/N)系數(shù)，根據(jù)歐拉公式，它是由cos(t)+jsin(t)構成，這些系數(shù)可以在進行計算前制作成表格提前得到，或者使用三角變換公式進行地推而形成，這都可以加快具體計算過程。

下面，對于上述方法進行實驗驗證一下。采用和以前實驗方案相同，在以前標準信號源回路中串入不同的電感，模擬不同長度的電磁線。通過一個LC諧振回路放在電磁線周圍，來感應磁場強度。分別記錄在不同串入電感的情況下，LC輸出交流電壓信號以及電流采集信號的FFT系數(shù)。

如下是對20中不同電感下，測量的數(shù)據(jù)曲線。可以看出，原來標準信號源，隨著輸出回路電感的增加，輸出電流信號的基波分量在逐步增加。具體原因在以往的推文中有分析。

與此同時，可以看到通過電流采樣數(shù)據(jù)所計算出的FFT基波分量的頻譜系數(shù)也按照相同的比例進行變化。

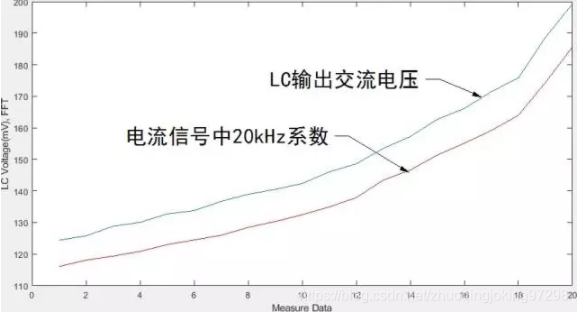
這說明，通過軟件計算所獲得的基波分量的大小與采用LC選頻諧振回路的作用相同。如果使用FFT系數(shù)對于輸出電流進行反饋控制，就可以使得輸出電流的基波保持穩(wěn)定。

如下就是使用采集到的LC電壓值除以電流信號的FFT基波系數(shù)所得到的比值，可以看到該比值基本維持在 一個恒定量。

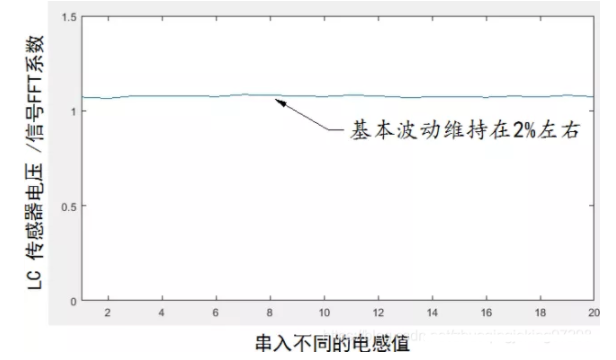
這也說明，使用電流采樣然后進行頻譜分析可以完成信號源基波分量的穩(wěn)定控制。

總結

對于比賽數(shù)字信號源增加輸出電流采樣電阻，通過信號欠采樣計數(shù)，可以獲得輸出電流波形數(shù)據(jù)。應用信號傅里葉變換，提取所感興趣的基波分量的幅度。由于只是計算基波分量 一個頻譜系數(shù)，所以不需要采用快速傅里葉變換，而是使用迭代的方式完成普通的離散傅里葉變換計算就可以高效計算出對應的頻譜系數(shù)。

在具體實現(xiàn)中有些參數(shù)需要通過試湊來完成優(yōu)化。比如欠采樣的頻率的選擇，計算DFT數(shù)據(jù)的長度等。在上述實驗，選擇欠采樣頻率使得在信號的一個周期內可以采集到100個左右的有效數(shù)據(jù)。為了避免由于數(shù)據(jù)截取對于計算結果所帶來的誤差，選擇1個或者2個正周期的數(shù)據(jù)進行計算，可以獲得比較穩(wěn)定的頻譜系數(shù)。

通過此次的分析，是否大家認為“信號與系統(tǒng)”課程的重要性了？
編輯：hfy