本文介紹了采用創(chuàng)建一個Python腳本，用該腳本模仿R風格的函數的方法來方便地進行統(tǒng)計。

是用R語言還是用Python語言？這是一個曠日持久的爭論。在此，我們可以嘗試采用折中路線：創(chuàng)建一個Python腳本，用該腳本模仿R風格的函數，來方便地進行統(tǒng)計！

簡介
用R語言還是用Python語言？這是數據科學和機器學習的一場大的爭論。毫無疑問，這兩種語言在最近幾年都取得了巨大的進展，成為數據科學、預測分析和機器學習的首選編程語言。事實上，在IEEE新近的一篇文章中，Python取代C++成為2018年的頂級編程語言，R已經牢牢地保住了它在前10名中的位置。

然而，這兩種編程語言之間存在著一些本質的差異。R主要是為數據分析問題的統(tǒng)計分析和快速原型化而開發(fā)的工具。另一方面，Python作為一種通用的現代面向對象語言，與C或Java相似，它具有更簡單的學習曲線和更為靈活的行為方式。因此，R在統(tǒng)計學家、定量生物學家、物理學家和經濟學家中仍然非常受歡迎，而Python逐漸成為日常腳本、自動化、后端web開發(fā)、分析和通用機器學習框架的首選語言，Python語言的技術支持基礎比較廣泛，同時還有許多開源社區(qū)。

如何在Python環(huán)境中模仿函數式編程？
R語言的函數編程特性為用戶提供了非常簡單有效地界面，用于快速計算概率，并為數據分析問題提供必要的描述性/推理統(tǒng)計。例如，僅僅使用一個緊致函數調用就能回答下面的問題，這是不是很神奇？

• 如何計算數據向量的平均/中值/模型？
• 如何計算服從正態(tài)分布的某一事件的累積概率？如果該分布是泊松分布，則如何計算？
• 如何計算一系列數據點的四分位數間距？
• 如何根據學生的t分布生成少量隨機數？

在R語言編程環(huán)境中，這些您都能實現。

另一方面，Python腳本編寫能使分析人員在各種分析管線中創(chuàng)造性地使用這些統(tǒng)計數據。

為了結合這兩種語言的優(yōu)勢，需要設計一個簡單的基于Python的包裝類庫，它包含最常用的函數，這些函數涉及以R風格定義的概率分布和描述性統(tǒng)計信息，用戶可以快速地調用這些函數，而無需調用Python統(tǒng)計庫，并弄明白所有方法和參數。

最為便捷的R-函數的Python包裝類腳本
我用Python編寫了一個腳本，用來定義在簡單統(tǒng)計分析中最為便捷和最被廣泛使用的R函數。導入這個腳本之后，您將能夠像在R編程環(huán)境中一樣自然地使用那些R-函數。

這個腳本的目標是利用簡單的Python子程序，來模仿R風格的統(tǒng)計函數，從而快速計算密度/點估計、累積分布、分位數，并為各種重要的概率分布生成隨機變量。為了保持R的風格，沒有使用類分層結構，只在該文件中定義了一些原始函數，這樣用戶便可以方便地導入這個Python腳本，并在需要時使用所有函數，而僅僅只需做一個名稱的調用。

注意，在此使用了“模仿”這個詞。我并沒有聲稱要模仿R真正的功能編程范式：那些由深層次的環(huán)境設置和這些環(huán)境與對象之間組成的復雜的相互關系。這個腳本只允許我(同時也希望有無數其他Python用戶)能夠快速啟動Python程序或Jupyter筆記本（一種交互式筆記本,支持運行 40 多種編程語言）導入腳本，并在短時間內開始進行簡單的描述性統(tǒng)計。這就是目標，僅此而已。

或者，你可能已經會用R語言編碼，剛開始學習和使用Python進行數據分析。你可以高興地看到和使用Jupyter筆記本里的一些眾所周知的函數，這些都和你使用的R語言環(huán)境中的方法類似。

簡單實例
例如，如果需要計算數據點向量的TuKEY五數綜合。你只需調用一個簡單函數FiVunm并傳遞給向量，它便在一個Numpy數組中返回五數綜合（最小值；第1四分位數(Q1)；中位數(Q2)；第3四分位數(Q3)；最大值。）。
lst=[20,12,16,32,27,65,44,45,22,18]
fivenum(lst)
> array([12. , 18.5, 24.5, 41. , 65. ])

或者，你想知道以下問題的答案：
假設一臺機器平均每小時輸出10件成品，標準差為2，輸出模式服從近似正態(tài)分布。在接下來的一小時內，機器輸出至少7臺但不超過12臺的概率是多少？

答案基本上是這樣，

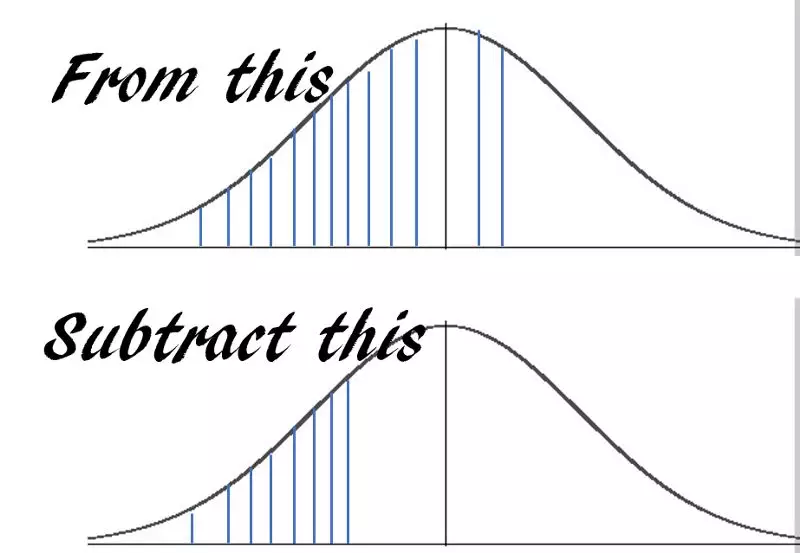
利用pNorm…，只需要一行代碼就可以得到答案。
pnorm(12,10,2)-pnorm(7,10,2)
> 0.7745375447996848

或者，對于如下問題：
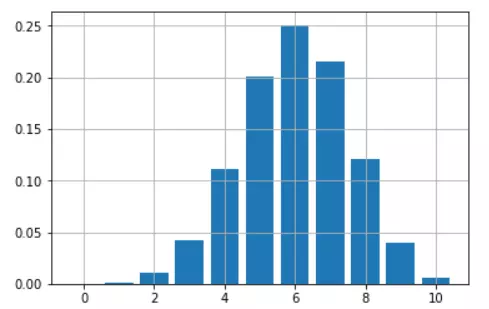
假設你有一枚硬幣，每次拋硬幣的時候，都有60%的轉動概率，玩的是10次拋擲的游戲。如何用這枚硬幣計算出所有可能的贏球數(從0到10)？

只需使用一個dbinom…函數和幾行代碼就可以獲得一個很好的條形圖。
probs=[]
import matplotlib.pyplot as plt
for i in range(11):
probs.append(dbinom(i,10,0.6))
plt.bar(range(11),height=probs)
plt.grid(True)
plt.show()

目前已經實現的函數
目前，已經實現了的、可以用于快速調用的R風格函數在以下腳本中實現。

• 均值、中值、方差、標準差
• TuKEY五數綜合、矩陣的IQR
• 矩陣的協(xié)方差或兩個向量之間的協(xié)方差
• 密度、累積概率、分位函數和隨機變量生成，用于下列分布：正態(tài)分布，均勻分布，二項分布，泊松分布，F分布，Student’s-t分布，卡方分布，Beta分布，和Gamma分布

后續(xù)工作
這項工作還正在進行之中，我計劃在腳本中添加一些更為便捷的R-函數。例如，在R單行命令中，lm可以得到一個最小二乘擬合模型，該模型具有所有必要的推斷統(tǒng)計量(P值、標準誤差等)。這將是多么的簡短和緊湊！另一方面，Python中的標準線性回歸問題通常是使用Scikit-Learning來解決，需要用到更多的腳本來實現它。我計劃使用Python的statsmodel后端結合這個單一函數線性模型來實現。