回到基本的力學或物理課程,有一個特定的示例總是用來引入振蕩:諧波運動。這種基本的周期性運動描述了最基本的振蕩類型,其中系統以正弦軌跡運動。盡管這是許多其他現象的數學基礎的基本主題,但電路和機械中的實際振蕩并不總是遵循純諧波運動。取而代之的是,振蕩可能是由復雜的頻率混合引起的,從而導致周期性行為,而不僅僅是正弦波。
PCB設計中當您分析具有非線性成分的復雜電路時,即使系統由純諧波源驅動,您也可能會注意到一系列復雜的振蕩行為。是什么原因導致這種行為,以及它如何影響電氣行為?如果您的系統中具有非線性組件,則需要使用一些基本模擬來了解不同的頻率將如何引起與諧波運動甚至混沌振蕩的偏差。閱讀更多內容以了解這些非諧波振蕩會在何處發生以及如何在不同類型的系統中產生。
為了更好地理解為什么系統可能表現出不穩定的行為,我們需要簡要回顧一下簡單的諧波運動是如何產生的。一旦我們看到了非線性在這些系統中發生的位置,就變得更加清楚如何無法通過插入正弦解簡單地解決非線性系統。
首先,我們有一個線性振蕩器的基本公式,如下所示。量u(t)可以是系統中的機械運動,電壓,電流或其他一些相關量。f(t)項是強迫函數,可以是時間的任何連續或分段函數。對于電氣系統,這是您用來描述RLC電路或以線性方式運行的非線性電路中的振蕩的方程式。
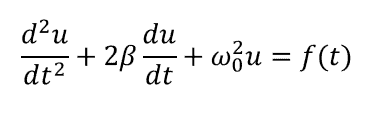
線性電路中的電壓,電流或功率受時間相關的強制功能驅動。
當f(t)=
-
pcb
+關注
關注
4322文章
23119瀏覽量
398473 -
振蕩器
+關注
關注
28文章
3838瀏覽量
139158
發布評論請先 登錄
相關推薦
PCB設計流程與PCB設計檢查表介紹
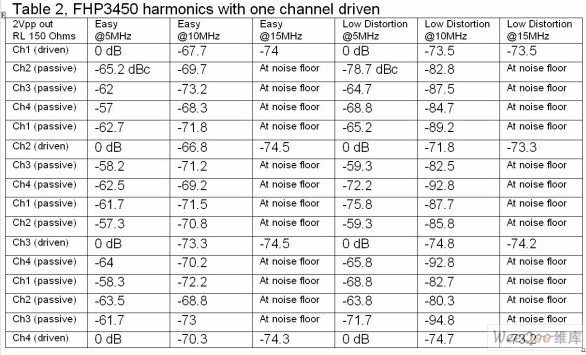
PCB設計時的諧波失真是如何產生的?
PCB設計中的過孔問題討論
減少諧波失真的PCB設計方法




 PCB設計中簡單諧波運動是如何產生的
PCB設計中簡單諧波運動是如何產生的












評論