有一個函數f(x),它的計算成本很高,甚至不一定是解析表達式,而且導數未知。你的任務是,找出全局最小值。當然,這個任務挺難的,比機器學習中的其他優化問題要難得多。例如,梯度下降可以獲得函數的導數,并利用數學捷徑來更快地計算表達式。
另外,在某些優化場景中,函數的計算成本很低。如果可以在幾秒鐘內得到數百個輸入值x的變量結果,簡單的網格搜索效果會更好。另外,還可以使用大量非傳統的非梯度優化方法,如粒子群算法或模擬退火算法(simulated annealing)。
但是,當前的任務沒有還沒這么高級。優化層面有限,主要包括:
計算成本高。理想情況下,我們能夠對函數進行足夠的查詢,從而從本質上復制它,但是采用的優化方法必須在有限的輸入采樣中才能起作用。
導數未知。梯度下降及其風格仍然是最流行的深度學習方法,甚至有時在其他機器學習算法中也備受歡迎的原因所在。導數給了優化器方向感,不過我們沒有導數。
需要找出全局最小值,即使對于梯度下降這樣精細的方法,這也是一項困難的任務。模型需要某種機制來避免陷入局部最小值。
我們的解決方案是貝葉斯優化,它提供了一個簡潔的框架來處理類似于場景描述的問題,以最精簡的步驟數找到全局最小值。
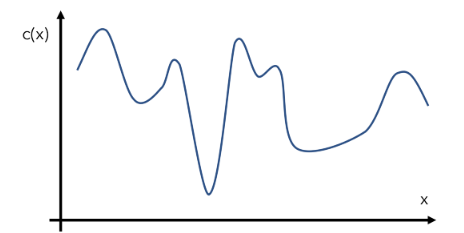
構造一個函數c(x)的假設例子,或者給定輸入值x的模型的成本。當然,這個函數看起來是什么樣子對優化器是隱藏的——這就是c(x)的真實形狀,行話中被稱為“目標函數”。
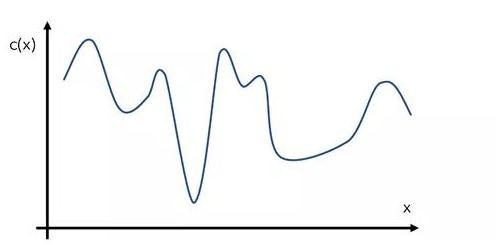
貝葉斯優化通過代理優化方法來完成這項任務。代理函數(surrogate function)是指目標函數的近似函數,是基于采樣點形成的。
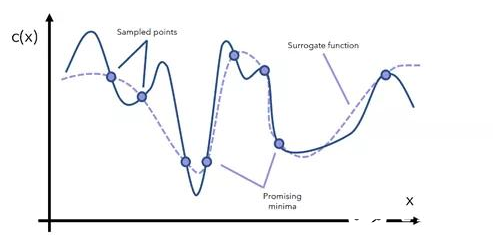
代理函數可以幫助確定哪些點是可能的最小值。我們決定從這些有希望的區域中抽取更多樣本,并相應地更新代理函數。
在每次迭代中繼續查看當前的代理函數,通過抽樣了解相關感興趣領域的更多信息并更新函數。注意,代理函數的計算成本要低得多。例如,y=x即是近似函數,計算成本更高,即在一定范圍內的y=arcsin((1-cos converx)/sin x))。
經過一定次數的迭代,最終一定會得到一個全局最小值,除非函數的形狀非常奇怪(因為它有大幅度且不穩定的波動),這時出現了一個比優化更有意義的問題:你的數據出了什么問題?
讓我們來欣賞一下貝葉斯優化之美。它不做任何關于函數的假設(除了首先假設它本身是可優化的),不需要關于導數的信息,并且能夠巧妙地使用一個不斷更新的近似函數來使用常識推理,對原始目標函數的高成本評估根本不是問題。這是一種基于替代的優化方法。
所以,貝葉斯理論到底是什么呢?貝葉斯統計和建模的本質是根據新信息更新之前的函數(先驗函數),產生一個更新后的函數(后驗函數)。這正是代理優化在本例中的作用,可以通過貝葉斯理論、公式和含義來進行最佳表達。
仔細看看代理函數,它通常由高斯過程表示,可以被視為一個骰子,返回適合給定數據點(例如sin、log)的函數,而不是數字1到6。這個過程返回幾個函數,這些函數都帶有概率。
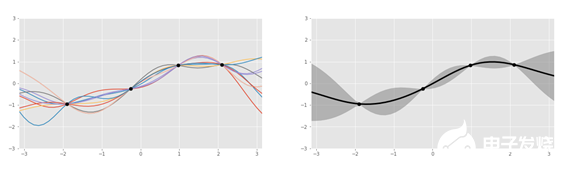
左:四個數據點的幾個高斯過程生成的函數。右:函數聚合。| 圖源:Oscar Knagg
使用GP而不是其他曲線擬合方法來建模代理函數,是因為它本質上是貝葉斯的。GP是一個概率分布,類似一個事件的最終結果的分布(例如,1/2的概率拋硬幣),但是覆蓋了所有可能的函數。
例如,將當前數據點集定義為40%可由函數a(x)表示,10%可由函數b(x)表示。通過將代理函數表示為概率分布,可以通過固有的概率貝葉斯過程更新信息。當引入新信息時,可能只有20%的數據可用函數a(x)表示。這些變化是由貝葉斯公式控制的。如果使用多項式回歸來擬合新的數據點,難度就加大了,甚至不可能實現。
代理函數表示為概率分布,先驗函數被更新為“采集函數”。該函數負責權衡探索和利用問題驅動新點的命題進行測試:
· “利用函數”試圖進行取樣以便代理函數預測最合適的最小值,這是利用已知的可能的點。然而,如果我們已經對某一區域進行了足夠的探索,那么繼續利用已知的信息將不會有什么收獲。
· “探索函數”試圖在不確定性高的地方取樣。這就確保了空間中沒有什么主要區域是未知的——全局最小值可能恰好就在那里。
一個鼓勵多利用和少探索的采集函數將導致模型只停留在它首先找到的最小值(通常是局部的——“只去有光的地方”)。反之,模型則首先不會停留在局部或全局的最小值上,而是在微妙的平衡中尋求最佳結果。
用a(x)表示采集函數,必須同時考慮探索和利用。常見的采集函數包括預期改進和最大改進概率,所有這些函數都度量了給定的先驗信息(高斯過程)下,特定輸入值在未來獲得成功的概率。
結合以上所有內容,貝葉斯優化的原理如下:
初始化一個高斯過程的“代理函數”先驗分布。
選擇多個數據點x,使運行在當前先驗分布上的采集函數a(x)最大化。
對目標成本函數c(x)中的數據點x進行評估,得到結果y。
用新的數據更新高斯過程的先驗分布,產生后驗(在下一步將成為先驗)。
重復步驟2-5進行多次迭代。
解釋當前的高斯過程分布(成本極低)來找到全局最小值。
貝葉斯優化就是把概率的概念建立在代理優化的基礎之上。這兩種概念的結合創造了一個功能強大的系統,應用范圍廣闊,從制藥產品開發到自動駕駛汽車都有相關應用。
然而,在機器學習中最常見的是用于超參數優化。例如,如果要訓練一個梯度增強分類器,從學習率到最大深度到最小雜質分割值,有幾十個參數。在本例中,x表示模型的超參數,c(x)表示模型的性能,給定超參數x。
使用貝葉斯優化的主要目的在于應對評估輸出非常昂貴的情況。首先,需要用這些參數建立一個完整的樹集合,其次,它們需要經過多次預測,這對于集合而言成本極高。
可以說,神經網絡評估給定參數集的損失更快:簡單地重復矩陣乘法,這是非常快的,特別是在專用硬件上。這就是使用梯度下降法的原因之一,它需要反復查詢來了解其發展方向。
圖源:unsplash
總結一下,我們的結論是:
· 代理優化使用代理函數或近似函數來通過抽樣估計目標函數。
· 貝葉斯優化通過將代理函數表示為概率分布,將代理優化置于概率框架中,并根據新信息進行更新。
· 采集函數用于評估探索空間中的某個點將產生“良好”結果的概率,給定目前從先驗已知的信息,平衡探索和利用的問題。
· 主要在評估目標函數成本昂貴時使用貝葉斯優化,通常用于超參數調優。有許多像HyperOpt這樣的庫可以實現這個功能。
貝葉斯優化之美,你感受到了嗎?
責編AJX
-
算法
+關注
關注
23文章
4629瀏覽量
93237 -
函數
+關注
關注
3文章
4345瀏覽量
62901 -
貝葉斯
+關注
關注
0文章
77瀏覽量
12585
發布評論請先 登錄
相關推薦
如何理解貝葉斯公式
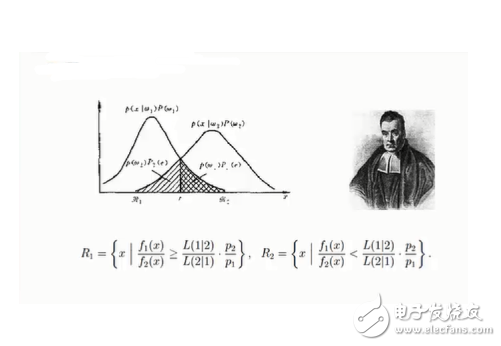
機器學習之樸素貝葉斯
一文秒懂貝葉斯優化/Bayesian Optimization





 理解貝葉斯優化之美,探索精妙算法的奧秘
理解貝葉斯優化之美,探索精妙算法的奧秘












評論