一、電路基礎
電壓電流
電流的參考方向可以任意指定,分析時:若參考方向與實際方向一致,則i》0,反之i0。
電壓的參考方向也可以任意指定,分析時:若參考方向與實際方向一致,則u》0反之u0。
功率平衡
一個實際的電路中,電源發出的功率總是等于負載消耗的功率。
全電路歐姆定律
U=E-RI
負載大小的意義
電路的電流越大,負載越大,電路的電阻越大,負載越小。
電路的斷路與短路
電路的斷路處:I=0,U≠0 電路的短路處:U=0,I≠0 。
二、基爾霍夫定律
幾個概念
支路:是電路的一個分支。
結點:三條(或三條以上)支路的聯接點稱為結點。
回路:由支路構成的閉合路徑稱為回路。
網孔:電路中無其他支路穿過的回路稱為網孔。
基爾霍夫電流定律
定義:任一時刻,流入一個結點的電流的代數和為零。或者說:流入的電流等于流出的電流。
表達式:i進總和=0 或:i進=i出。
可以推廣到一個閉合面。
基爾霍夫電壓定律
定義:經過任何一個閉合的路徑,電壓的升等于電壓的降。
或者說:在一個閉合的回路中,電壓的代數和為零。
或者說:在一個閉合的回路中,電阻上的電壓降之和等于電源的電動勢之和。
電位的概念
定義:某點的電位等于該點到電路參考點的電壓。
規定參考點的電位為零。稱為接地。
電壓用符號U表示,電位用符號V表示
兩點間的電壓等于兩點的電位的差 。
注意電源的簡化畫法
三、理想電壓源與理想電流源
理想電壓源
不論負載電阻的大小,不論輸出電流的大小,理想電壓源的輸出電壓不變。理想電壓源的輸出功率可達無窮大。
理想電壓源不允許短路。
理想電流源
不論負載電阻的大小,不論輸出電壓的大小,理想電流源的輸出電流不變。理想電流源的輸出功率可達無窮大。
理想電流源不允許開路。
理想電壓源與理想電流源的串并聯
理想電壓源與理想電流源串聯時,電路中的電流等于電流源的電流,電流源起作用。
理想電壓源與理想電流源并聯時,電源兩端的電壓等于電壓源的電壓,電壓源起作用。
理想電源與電阻的串并聯
理想電壓源與電阻并聯,可將電阻去掉(斷開),不影響對其它電路的分析。
理想電流源與電阻串聯,可將電阻去掉(短路),不影響對其它電路的分析。
實際應用中的電壓源和電流源
實際的電壓源可由一個理想電壓源和一個內電阻的串聯來表示。
實際的電流源可由一個理想電流源和一個內電阻的并聯來表示。
四、支路電流法
意義
用支路電流作為未知量,列方程求解的方法。
列方程的方法
1. 電路中有b條支路,共需列出b個方程。
2. 若電路中有n個結點,首先用基爾霍夫電流定律列出n-1個電流方程。
3. 然后選b-(n-1)個獨立的回路,用基爾霍夫電壓定律列回路的電壓方程。
注意問題
若電路中某條支路包含電流源,則該支路的電流為已知,可少列一個方程(少列一個回路的電壓方程)。
五、疊加原理
意義
在線性電路中,各處的電壓和電流是由多個電源單獨作用相疊加的結果。
求解方法
考慮某一電源單獨作用時,應將其它電源去掉,把其它電壓源短路、電流源斷開。
注意問題
最后疊加時,應考慮各電源單獨作用產生的電流與總電流的方向問題。
疊加原理只適合于線性電路,不適合于非線性電路,只適合于電壓與電流的計算,不適合于功率的計算。
六、戴維寧定理
意義
把一個復雜的含源二端網絡,用一個電阻和電壓源來等效。
等效電源電壓的求法
把負載電阻斷開,求出電路的開路電壓UOC。等效電源電壓UeS等于二端網絡的開路電壓UOC。
等效電源內電阻的求法
把負載電阻斷開,把二端網絡內的電源去掉(電壓源短路,電流源斷路),從負載兩端看進去的電阻,即等效電源的內電阻R0。
把負載電阻斷開,求出電路的開路電壓UOC。然后,把負載電阻短路,求出電路的短路電流ISC,則等效電源的內電阻等于UOC/ISC。
七、諾頓定理
意義
把一個復雜的含源二端網絡,用一個電阻和電流源的并聯電路來等效。
等效電流源電流IeS的求法
把負載電阻短路,求出電路的短路電流ISC。則等效電流源的電流IeS等于電路的短路電流ISC。
等效電源內電阻的求法
同戴維寧定理中內電阻的求法。
八、換路定則
換路原則
換路時:電容兩端的電壓保持不變,Uc(o+) =Uc(o-)。電感上的電流保持不變, Ic(o+)= Ic(o-)。原因是:電容的儲能與電容兩端的電壓有關,電感的儲能與通過的電流有關。
換路時,對電感和電容的處理
換路前,電容無儲能時,Uc(o+)=0。換路后,Uc(o-)=0,電容兩端電壓等于零,可以把電容看作短路。
換路前,電容有儲能時,Uc(o+)=U。換路后,Uc(o-)=U,電容兩端電壓不變,可以把電容看作是一個電壓源。
換路前,電感無儲能時,IL(o-)=0。換路后,IL(o+)=0,電感上通過的電流為零,可以把電感看作開路。
換路前,電感有儲能時,IL(o-)=I。換路后,IL(o+)=I,電感上的電流保持不變,可以把電感看作是一個電流源。根據以上原則,可以計算出換路后,電路中各處電壓和電流的初始值。
九、正弦量的基本概念
正弦量的三要素
表示大小的量:有效值,最大值。
表示變化快慢的量:周期T,頻率f,角頻率ω。
表示初始狀態的量:相位,初相位,相位差。
復數的基本知識
復數可用于表示有向線段,復數A的模是r ,輻角是Ψ。
復數的表示方式:1.代數式;2.三角式;3.指數式;4.極坐標式。
復數的加減法運算用代數式進行,復數的乘除法運算用指數式或極坐標式進行。
復數的虛數單位j的意義:任一向量乘以+j后,向前(逆時針方向)旋轉了,乘以-j后,向后(順時針方向)旋轉了。
十、正弦量的相量表示法
相量的意義
用復數的模表示正弦量的大小,用復數的輻角來表示正弦量初相位。相量就是用于表示正弦量的復數。為與一般的復數相區別,相量的符號上加一個小圓點。
最大值相量
用復數的模表示正弦量的最大值。
有效值相量
用復數的模表示正弦量的有效值。
注意問題
正弦量有三個要素,而復數只有兩個要素,所以相量中只表示出了正弦量的大小和初相位,沒有表示出交流電的周期或頻率。相量不等于正弦量。
用相量表示正弦量的意義
用相量表示正弦后,正弦量的加減,乘除,積分和微分運算都可以變換為復數的代數運算。相量的加減法也可以用作圖法實現,方法同復數運算的平行四邊形法和三角形法。
十一、交流電路的功率
瞬時功率:
p=ui=UmIm·sin(ωt+φ)·sinωt=UIcosφ-UIcos(2ωt+φ)。
平均功率:P=UIcosφ平均功率又稱為有功功率,其中 cosφ稱為功率因數。電路中的有功功率也就是電阻上所消耗的功率。
無功功率:Q=ULI-UCI= I2(XL-XC)=UIsinφ電路中的無功功率也就是電感與電容和電源之間往返交換的功率。
視在功率:S=UI 視在功率的單位是伏安(VA),常用于表示發電機和變壓器等供電設備的容量。
功率三角形:P、Q、S組成一個三角形,其中φ為阻抗角。
十二、電路的功率因數
功率因數的意義
功率因數就是電路的有功功率占總的視在功率的比例,從功率三角形中可以看出功率因數。
功率因數高,則意味著電路中的有功功率比例大,無功功率的比例小。
功率因數低的原因
生產和生活中大量使用的是電感性負載異步電動機,洗衣機、電風扇、日光燈都為感性負載。
電動機輕載或空載運行(大馬拉小車),異步電動機空載時cosφ=0.2~0.3,額定負載時cosφ=0.7~0.9。
提高功率因數的意義
在電感性負載兩端并聯電容可以補償電感消耗的無功功率,提高電路的功率因數。
提高發電設備和變壓器的利用率:發電機和變壓器等供電設備都有一定的容量,稱為視在功率,提高電路的功率因數,可減小無功功率輸出,提高有功功率的輸出,增大設備的利用率。
降低線路的損耗:當線路傳送的功率一定,線路的傳輸電壓一定時,提高電路的功率因數可減小線路的電流,從而可以降低線路上的功率損耗,降低線路上的電壓降,提高供電質量,還可以使用較細的導線,節省建設成本。
責任編輯:haq
-
電源
+關注
關注
184文章
17803瀏覽量
251010 -
電阻
+關注
關注
86文章
5536瀏覽量
172385 -
電容
+關注
關注
100文章
6073瀏覽量
150642 -
電壓
+關注
關注
45文章
5622瀏覽量
116016
發布評論請先 登錄
相關推薦
【電路小知識】交流電路基礎知識和波形的種類
全新的半導體基礎知識
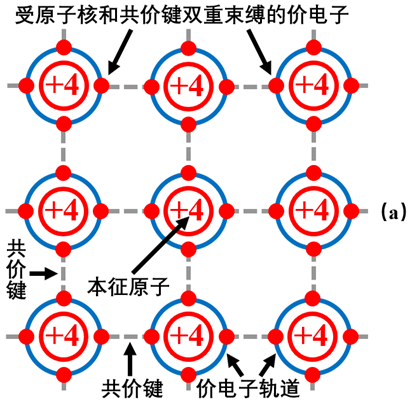
模擬電路基礎知識(2)
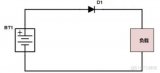




 十二個電路基礎知識匯總
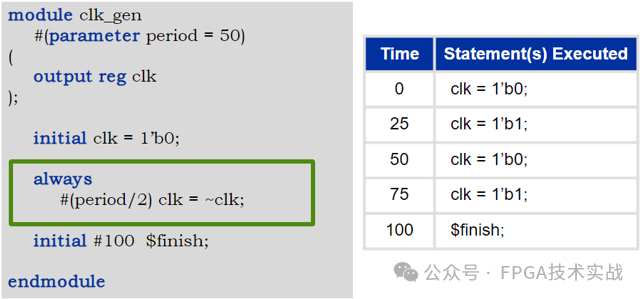
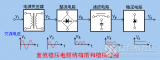
十二個電路基礎知識匯總














評論