2020年10月16日下午，中共中央政治局舉行第二十四次集體學習，主題是“量子科技研究和應用前景”。為更好地了解國內外量子密碼科技發展態勢，更好地推進我國量子科技發展，本專委會邀請廣東工業大學的教授專門撰文介紹后量子密碼技術。

一、后量子密碼技術的發展歷程

后量子密碼技術是指可以抵抗量子計算機攻擊的密碼技術。所謂“后”，是指在大規模穩定的量子計算機出現后，現有的絕大多數公鑰密碼算法（RSA、Diffie-Hellman、橢圓曲線等）將會被攻破，只有能抵抗這種攻擊的密碼算法可以在進入量子計算時代之后存活，因此也稱為“抗量子密碼技術”。

近年來，量子計算機的發展非常迅速，許多大學或企業如加州大學、Google、IBM、Intel等為之都投入了大量人力物力［1］。

2007年，加拿大一家名為D-Wave System的公司已經造出了一臺量子計算機D-Wave，盡管人們還在爭論這臺計算機是否能達到原理上所要求的特性與效果（即無法使所有量子比特發生糾纏），但NASA和Google已經測試出這臺計算機在解決某些問題上比傳統的單核計算機快1億倍 ［2］。

2014年，Google的研究團隊宣布建成9量子比特的可編程量子機器，直到2018年3月，該研究團隊發布了新的72量子比特的量子處理器Bristlecone，標志著量子計算技術的發展進入了一個極速發展的階段。與此同時，IBM公司也宣稱他們已經成功開發出一臺50量子比特的原型機，該50量子比特的量子計算機能模擬傳統計算機的所有操作。

在國內，2017年5月，阿里巴巴與中科院、中科大合作團隊研發出10 量子比特的線路樣品。

2018年2月，阿里合作團隊宣布11量子比特超導量子計算服務將在阿里的量子計算云平臺上線。

一般來說，密碼系統在開發過程中都會考慮到破解其的計算技術發展的速度和水平，傳統密碼的安全性依賴于某些問題對現代計算機的難解性，例如，RSA依賴于大數因式分解難題。傳統的計算機采用二進制數即0和1來處理信息，因此處理一個1024位的大數（0-21024）因式分解是一個難解問題。但量子計算機不同，它利用量子力學，并使用 “量子位元”而不是0和1來處理信息。因此，在處理大數因子分解時，量子計算機會有更好的效果。圖1展示了量子計算機對現有密碼標準的影響。

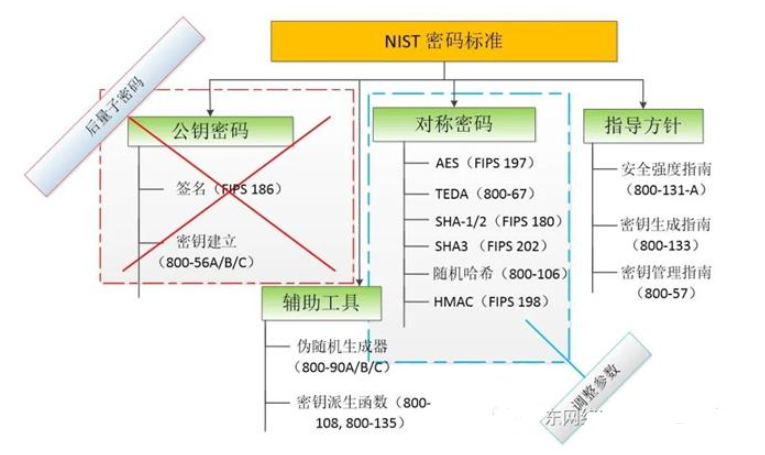
圖1 量子計算機對現有密碼標準的影響

其中：紅色叉，代表量子計算機可以完全攻破，需要后量子密碼算法代替；藍色框，不那么緊迫需要新算法代替，可以通過調整算法參數解決。

總的來說，量子計算機對現有密碼標準的影響有以下幾個要點：

1.對于公鑰密碼算法，量子計算機對安全性的影響包括：

（1）完全攻破目前廣泛使用的公鑰密碼算法。公鑰密碼算法安全性依賴的數學問題可以被高效的量子算法所解決。由于底層依賴的數學問題被解決，所以這些公鑰密碼算法不再安全。這些數學問題包括：離散對數 （及橢圓曲線版本）、大整數分解等。這直接影響目前使用的 RSA、Diffie-Hellman、橢圓曲線等算法。著名的量子算法是1994年的Shor‘s algorithm［4］。

（2）增大密鑰參數的長度沒有用。增大密鑰長度對于現有的傳統計算機和攻擊算法是可以的，但對于量子計算機和算法，這是徒勞的。

（3）需要全新的公鑰密碼算法即后量子密碼算法。

2.對于對稱密碼算法，量子計算機對安全性的影響：

（1）降低現有算法的安全性：安全性減半。關于對稱密碼算法和哈希函數（例如 AES、SHA1、SHA2 等），雖然有量子算法可以理論上攻破，但這個算法的影響有限，且有很多限制條件。著名的量子算法是1996年的Grover’s algorithm［5］，可將安全性從k-bit 降低為k/2-bit。

（2）增大參數的長度有用，把密鑰長度或哈希的長度加倍即可，例如：AES-128升級至AES-256，SHA-256升級至SHA-512等。

3.量子計算機具有強大的算力，但利用的前提是：存在能高效解決問題的量子算法，否則量子計算機沒什么用，反而因為其高昂的成本帶來劣勢。

4.量子比特數量重要，但更重要的是質量。目前建造的量子計算機（例如 Google 的 72 量子位芯片）中，量子物理比特的質量較差。由于量子相干等物理機制，必須引入糾錯機制，但需要成百上千個量子物理比特進行糾錯，來實現一個量子邏輯比特的功能。

5.攻破現有的公鑰密碼算法需要幾千甚至幾萬個邏輯比特，而建造量子計算機目前仍處在很初級的階段。

6.對于某些量子算法（例如 Grover），需要指數級別的內存，因此 Grover 算法的威脅不如Shor的算法那么緊迫。

二、后量子密碼的技術現狀

密碼學界在研究可以抵抗量子計算機攻擊的密碼算法方面，最早可以追溯到 1978年的 McEliece加密、Merkle哈希簽名等算法。但那時量子計算機對密碼算法的威脅并沒有很明確，也沒有“后量子”的概念，直到最近十幾年，后量子密碼的重要性逐漸顯現出來。

2016年秋，美國國際標準技術研究所（NIST）發布后量子領域標準化方案征求稿［6］，正式在全球范圍征集后量子密碼學標準協議。2017年12月，NIST公布后量子密碼學標準協議的第一輪預選協議，協議均為后量子密碼學基礎方案，即加密（含密鑰交換KE或密鑰封裝KEM）和簽名方案。此次共收到82個基礎方案，其中公開69個被認為是完整的方案，隨后6個被撤銷。第一輪標準中基于格的密碼學方案有26個，基于編碼的密碼學方案有18個，多變量密碼學方案有9個，基于哈希的密碼學方案有3個，以及其他類型密碼學方案有7個。具體情況如表1所示。

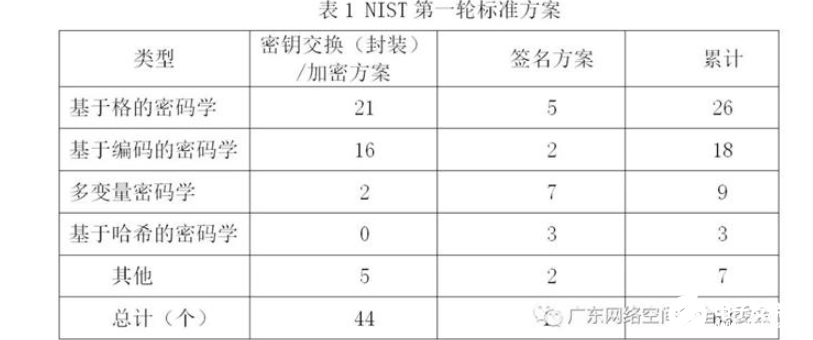
2018年11月，NIST再次發布第二輪的標準方案，從第一輪標準方案以及最新研究成果中遴選出26個進入第二輪，其中包括17個公鑰加密和密鑰交換方案及9個數字簽名方案。具體情況如表2所示。

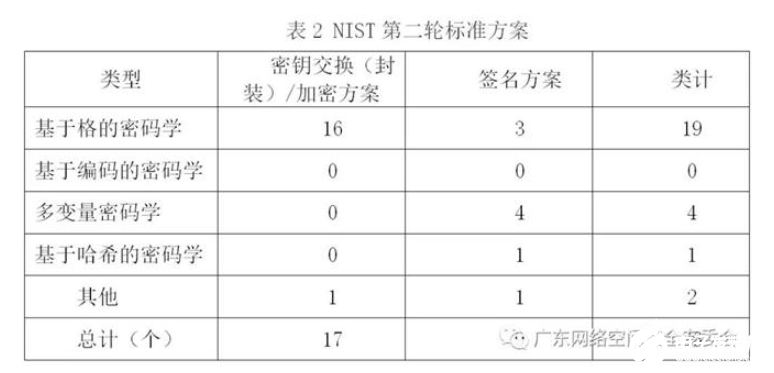
在NIST候選方案中，主要包括以下四種數學方法構造的后量子密碼算法：基于哈希的公鑰密碼學、基于編碼的公鑰密碼學、基于多變量的公鑰密碼學以及基于格的公鑰密碼學。

1. 基于哈希 （Hash-based）的公鑰密碼學

基于哈希的簽名算法最早出現于1979年，被認為是傳統數字簽名 （RSA、DSA、ECDSA等）的可行代替算法之一［7］。該方案使用哈希函數的輸入作為私鑰，輸出作為公鑰。這些密鑰僅適用于一個簽名，因為簽名本身會顯示密鑰的一部分。基于哈希的簽名會使用Merkle樹認證機制來減少空間消耗。使用Merkle樹認證后，哈希樹的根是公鑰，一次性的簽名密鑰是樹中的葉子節點。基于哈希的簽名算法的安全性依賴哈希函數的抗碰撞性，由于沒有有效的量子算法能快速找到哈希函數的碰撞，因此（輸出長度足夠長的）基于哈希的構造可以抵抗量子計算機攻擊。此外，基于哈希的數字簽名算法的安全性不依賴某一個特定的哈希函數。即使目前使用的某些哈希函數被攻破，也可以用更安全的哈希函數直接代替被攻破的哈希函數。

例如，一個經典的基于哈希的簽名方案設計如下圖2所示。

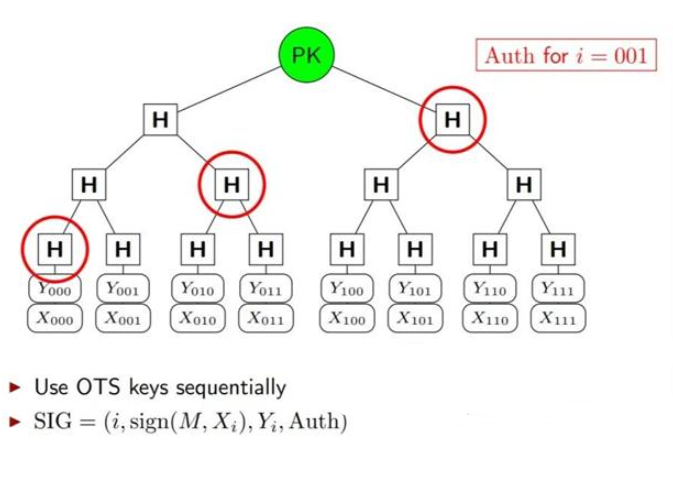
圖2 基于哈希的簽名方案設計圖

方案中的Xi和Yi分別為一次性密鑰的私鑰和公鑰，對消息的簽名增加了兩個狀態參數i和Auth，i用來保證所有葉子不會被使用超過1次，Auth是路徑，用來存儲中間結果，能使簽名快速運行。

基于哈希的代表算法有：Merkle 哈希樹簽名、XMSS、Lamport簽名等。

2.基于編碼 （Code-based） 的公鑰密碼學

基于編碼的算法最早出現于1978年，主要用于構造加密算法。目前技術方向主要分為兩種：基于海明度量（Hamming metric）的編碼方案和基于秩度量（Rank metric）的編碼。

基于海明度量的編碼方案的數學困難假設是校驗子譯碼問題（Syndrome Decoding Problem）。校驗子譯碼問題已被證明為NP完全（NP-Complete）問題［8］。此方向一個著名的加密算法是 McEliece ［9］，該方案使用了Goppa Codes，迄今為止仍然是安全的設計方案。但該方案最大的缺點就在于其公鑰需要1MB左右的大小才能達到256bit的安全度。

目前NIST標準預選方案中，大部分是基于秩度量的編碼方案。基于此技術而建構的加密或密鑰交換方案包括Loi17［10］、RQC［11］、ROLLO［12］、LG［13］和McNie ［14］等等。我國在秩度量加密方案的設計方面也有進展，如中科院信工所研究員設計的兩項加密方案：Piglet［15］和Loong［16］。

基于編碼的代表算法有：McEliece、Loi17、ROLLO等。

3. 基于多變量 （Multivariate-based） 的公鑰密碼學

基于多變量的算法使用有限域上具有多個變量的二次多項式組構造加密、簽名、密鑰交換等算法［17］。多變量密碼的安全性依賴于求解非線性方程組的困難程度，即多變量二次多項式問題。該問題已被證明為非確定性多項式時間（NP）困難。目前沒有已知的經典和量子算法可以快速求解有限域上的多變量方程組。與經典的基于數論問題的密碼算法相比，基于多變量的算法的計算速度快，但公鑰較大，因此適用于無需頻繁進行公鑰傳輸的應用場景（如物聯網設備等）。

多變量密碼的基礎方案設計就形式來說，可以分為兩種形式。

一種是既基于MQ 又基于IP （Isomorphism of Polynomials，多項式同構）問題的MPKC 加密或簽名方案設計，該方向的設計思路和密碼分析方法等都較為成熟，因而產生了較多的研究成果，如Rainbow［18］，UOV［19］，LUOV［20］，PFlash［21］等，以及近年基于大域上變量平方構造的SQUARE［22］，EFC［23］，使用了雙重HFE 的ZHFE［24］，Simple Matrix（ABC）加密方案［25］，Cubic ABC 加密方案［26］，基于中間域（大域小域特點結合的思想）的多變量加密方案有中國的［27］［28］等。

另一種是基于新設計思路、困難問題的方案設計。雖然目前基于IP問題設計MPKC方案依然是主流，但在設計思路與安全分析都相對成熟的情況下，取得突破性的成就反而不容易。因此MPKC 也需要提出一些新的設計思路，提出一些新的困難性假設來保持這個領域的活力和創新性。比如在PKC2012，有文獻結合格密碼中LWE的一些特性提出了一種新的困難性假設問題［29］，并在此困難性假設下提出了一種安全的加密方案。而在2014 年的Asia crypt會上有學者提出了一種不同于IP或者IP1S 的全新MPKC 設計結構ASASA ［30］，設計結合了對稱密碼中的S盒（使用二次多項式構造）以及A（仿射的）的構造特點。在國際頂級會議CRYPTO 2011 上，則有文獻提出了一種身份識別方案［31］，它的安全性依賴于非交互的承諾方案的存在性， 并給出了形式化的可證安全。從該身份識別方案出發，有學者通過Fiat-Shamir轉換構造了后量子第一輪標準簽名方案MQDSS［32］。該類型的密碼方案還包括最近基于新困難問題的第一輪標準協議Giophantus［33］。此外，我國方面，基于Hyper-Sphere 超球面方程的多變量方案則可以用于群組簽名的設計并提出了相關的安全性證明［34］，武漢大學有教授提出了一個可證安全的基于多項式同態（Morphism of polynomials， MP）的密鑰交換協議［35］等等。

基于多變量的代表算法有：LUOV、Rainbow、MQDSS等。

4. 基于格 （Lattice-based） 的公鑰密碼學

在后量子加密的所有方法中，對格的研究是最活躍和最靈活的。這是因為基于格的算法在安全性、公私鑰大小、計算速度上達到了更好的平衡［36］。與基于數論問題的密碼算法構造相比，基于格的算法可以實現明顯提升的計算速度、更高的安全強度和略微增加的通信開銷 ［37］。與其他幾種實現后量子密碼的方式相比，格密碼的公私鑰更小，并且安全性和計算速度等指標更優。此外，基于格的算法可以實現加密、數字簽名、密鑰交換、屬性加密、函數加密、全同態加密等各類功能的密碼學構造。

基于格的算法的安全性依賴于求解格中問題的困難性。這些問題在達到相同的安全強度時，基于格的算法的公私鑰大小比上述三種結構的方法更小，計算速度也更快，且能被用于構造多種密碼學原語，因此更適用于真實世界中的應用。

近年來，基于LWE（Learning with Errors） 問題 ［38］ 和 RLWE （Ring-LWE） 問題［39］的格密碼學構造發展迅速，被認為是最有希望被標準化的技術路線之一。

基于格的代表算法有：Kyber、Dilithium、NTRU系列、NewHope（Google 測試過）、一系列同態加密算法 （BGV、GSW、FV等）。

下表中給出了四種后量子密碼算法的簡要對比：

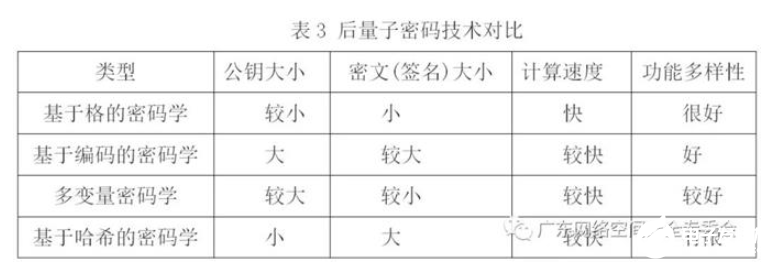
表中的對比反映出該類后量子密碼算法的平均性能指標。在實際應用中具體采用哪個類別/哪個算法更好，需要針對應用場景進行詳細分析。例如，在一些頻繁需要交換公鑰的場景（例如 HTTPS），可以使用 Lattice-based 的算法等。

除這四種類型的后量子密碼技術之外，還有基于超奇異橢圓曲線 （Supersingular elliptic curve isogeny）、量子隨機漫步 （Quantum walk）等技術的后量子密碼構造方法。

三、后量子密碼的發展前景

近年來，歐洲國家的“安全密碼”（SafeCrypto）項目和日本的CREST密碼數學項目都取得了顯著成果，美國NIST的“后量子密碼”（PQCrypto）項目和處于后量子密碼研究和應用領域的領先地位。

對于后量子密碼的發展前景大致如下。

1. 公鑰密碼系統向后量子密碼系統的穩步推進

傳統計算技術和量子計算技術的進步，推動了對更強大密碼技術的需求。為了抵御對傳統計算的攻擊，NIST已經建議從提供80位安全性的密鑰大小和算法過渡到提供112位或128位安全性的密鑰大小和算法。而為了提供抵御量子攻擊的安全性，未來還需要進行一個過渡，即把公鑰密碼系統過渡到新的后量子密碼系統。

歐洲電信標準協會與加拿大滑鐵盧大學量子計算中心聯合舉辦的量子安全密碼工作組會議（IQC/ETSI Quantum-Safe Crypto Workshop）也在國際后量子密碼研究領域產生了重要影響。該會始于2013年，參會代表來自于數學、密碼學、物理學、計算機等不同研究領域，目標是實現標準化和部署下一代密碼基礎設施，特別是抵御量子計算能力威脅的沖擊。

2. 后量子密碼技術標準制定逐步受到政府組織的重視

后量子密碼學標準的制定將需要大量的資源分析候選的抗量子計劃，為了確保對算法的信任，需要大量的研究人員參與密碼分析。國際上對量子計算和后量子密碼學領域的興趣最近有所增加，這跟量子計算硬件的發展和各國國家安全局最近對后量子標準的政策制定有關，大致總結如下。

美國方面，2015年8月，美國國家安全局公開宣布由于面臨量子計算的威脅，其計劃將聯邦政府各部門目前使用的ECC/RSA算法體系向后量子算法進行遷移。而負責標準制定的NIST則在2016年2月正式面向全球公開了后量子密碼標準化的路線圖，并在同年秋正式公布征集密碼方案建議的計劃，其中包括公鑰密碼、數字簽名以及密鑰交換算法。2017年12月獲得第一輪的建議方案；2018年12月征集后得到第二輪的建議方案；NIST會利用3-5年時間分析這些建議并發布相關分析報告，最終的標準擬制工作也將耗時1-2年。換言之，美國國家標準與技術局的后量子密碼算法標準最終可能會在2021-2023年出臺。

歐洲量子密碼學術和工業界研究者聯合組織“后量子密碼”項目（PQCrypto）在2015年發布了一份初始報告，在對稱加密、對稱授權、公鑰加密以及公鑰簽名系統領域都提出了相關標準化建議。

我國方面，從2018年12月開始，中國密碼學會在國家密碼管理局的指導下，啟動全國密碼算法設計競賽［40］，其中包含分組密碼算法設計和公鑰密碼算法設計兩部分。而后者則主要是后量子密碼算法的設計，當年即收到第一輪共38個公鑰密碼算法設計，并于2019年10月從中遴選出第二輪12個算法。

3. 企業界將在后量子密碼發展應用過程中發揮重要影響力

從以往的密碼系統標準化發展歷史來看，任何密碼系統都必須在應用過程中增強和完善性能，后量子密碼也不例外。因此，通過新型密碼產品的商業化推廣使用活動，企業界能夠不斷積累和分析用戶數據，從而促進后量子密碼系統安全性能和運行效應的提升。

美國安全創新公司（Security Innovation）注冊并擁有NTRU算法的專利，其提供兩種授權選項：開源GNUGPL v2授權以及商業授權。從2011年起，該公司發布了多種實現NTRU算法的軟件庫，其中包括安全套接字協議層（SSL）和ARM7/9處理器庫等。NTRU工程（NTRUProject）網站中已經存在使用NTRU加密算法的Java和C程序應用。目前，NTRU算法已經在處理能力有限的移動設備以及大容量服務器中得到應用。

微軟公司2016年發布了基于格密碼庫（Lattice Crypto），這種可移植軟件的底層機制是基于環上帶誤差學習問題（Ring Learning With Errors）。無論對于使用經典計算機或者量子計算機的攻擊者，該軟件庫至少能夠實現128位安全性能。谷歌公司在對當前后量子密碼技術發展進行調查后，也提出了基于環上帶誤差學習問題的密鑰交換協議。這些工作都對量子密碼系統的標準化具有重要影響。
編輯：hfy