這次初步聊一聊 ADC 的相關知識。
BMS 中會用到 ADC,例如集成在單片機內部的,或者獨立的;比較有代表性的就是 AFE 中的 ADC,由于 AFE 做了太多的工作,反而弱化了大家對其 ADC 的感知。
在 AFE 中主要存在兩種類型的 ADC:即 SAR 型與 Sigma-Delta 型,下面分別介紹。
SAR 型 ADCSAR(Successive approximation register),即逐次逼近型 ADC,例如美信的 MAX17823 使用的就是此類型 ADC。
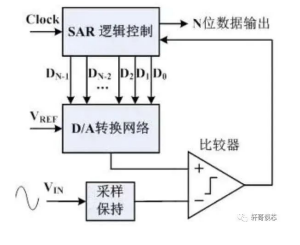
一個基本的逐次逼近型 ADC 的原理框圖如下:由采樣保持電路(SHA)、控制邏輯電路、時序發生電路、D/A 轉換電路、電壓比較電路等組成。
基本原理類似天平稱重:如下圖所示,假設一個 6bit 的 SAR ADC,則全量程的數字量為 64,為容易理解,假設對應的模擬量也是 64。
那么對模擬量 X=45 進行 AD 轉換:首先將 X 與 32 進行比較(0.5 倍 FSR,通過 DAC 設置),因為 X>32,則對應最高 bit 位置為 1;接著 X 與 48 進行比較(0.75 倍 FSR),因為 X<48,則次高位置 0;以此方法繼續向下類推,最后得到一個 6 位的二級制代碼。即 X=101101,這樣就完成了模擬量到數字量的過程。Sigma-Delta 型 ADC 也稱作Σ-Δ型 ADC,當然也有人叫做Δ-Σ型 ADC,實際這兩種叫法都有人在用,前者可能更貼切;SAR 型 ADC 是直接測量模擬量,而Σ-Δ型 ADC 是屬于間接測量模擬量。在 ADI 的 LTC68XX 系列使用的就是此種類型 ADC,內部帶有可編程的數字濾波器。
一個典型的Σ-Δ型 ADC 原理框圖如下:包括了一個簡單的模擬調制電路(積分器、比較器、開關、DAC、求和電路)和一個復雜的數字電路(數字濾波器、數字信號處理器);其中這個模擬調制電路將模擬信號轉換為數字 bit 流,而數字電路進一步把數字 bit 流轉換為代表模擬輸入幅值的數字編碼。
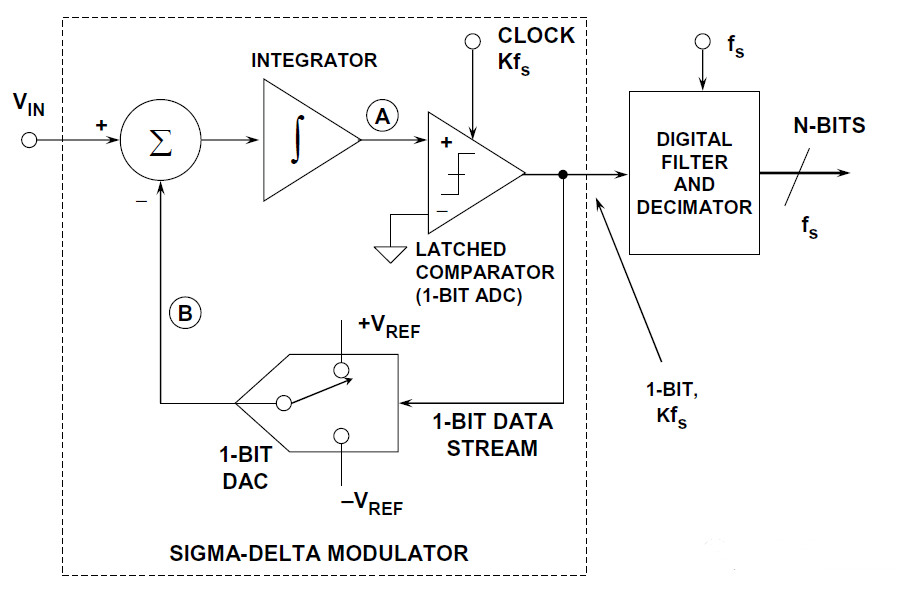
Σ-Δ型 ADC 的信號轉換流程如下圖:把模擬輸入電平最終轉換成了數字量輸出,根據數字量輸出大小,可以換算出模擬量的幅值。
進一步地,單獨把模擬調制部分拿出來,如下圖:
我們仔細看上圖,其實整個環路是一個負反饋的閉合回路;由于負反饋的存在,X5 處的電平總是抑制積分器的累加值輸出 X3 在 0V 上下波動,這樣其實理論上 X5 處的平均值就等于輸入信號 X1,時間越長,X5 的平均值越接近 X1;而這種關系其實是映射到了 X4 處輸出的 1 的個數。
下面為實際的例子,假設輸入 X1 為 0 或 0.5*Vref,波形 A 為積分器輸出 X3,波形 B 為比較器輸出 X4,就有如下的對應關系:1 的數量越多,代表 X1 越大。
具體計算的話,以上圖中的輸入 X1=0.5Vref 為例,我們在輸出信號 X4 處取 4 個采樣點,其中有 3 個 1 和 1 個 0,那么轉換為模擬量=3/4*2*Vref-Vref=0.5Vref,與輸入 X1 相等。
當你的采樣點數量越多,轉換出來的值就越準確,所以Σ-Δ型 ADC 就會進行過采樣,這也就造成了其轉換速度慢的特點。假如輸入是一個正弦波,那么此時 X1 與 X4 的對應關系就如下圖:同樣地,1 的密度大的地方代表 X1 幅值大。
后面的數字電路部分就針對前面得到的 bit 流進行濾波、抽樣、處理等操作,最終得到一個 AD 量輸出給單片機。
這里再簡單提一下Σ-Δ型 ADC 為什么精度高?如下圖,左圖是普通的 ADC 量化產生的噪聲水平,右邊是Σ-Δ型 ADC 量化產生的噪聲水平,一目了然,Σ-Δ型 ADC 更加優秀;至于怎么推導出來的就比較復雜了,先記住這個結論即可。
總結:
話說查資料時,一定不能只輸入 ADC,要不查出來都是英雄聯盟相關的內容;ADC 的分類有很多種的,我只挑選了兩種有代表性的拿出來學習;以上所有,僅供參考。
編輯:hfy
-
單片機
+關注
關注
6037文章
44562瀏覽量
635754 -
adc
+關注
關注
98文章
6503瀏覽量
544817 -
信號轉換器
+關注
關注
0文章
79瀏覽量
13915
發布評論請先 登錄
相關推薦
逐次逼近型AD前端運放電路如何設計,運放的SNR是否必須比AD的SNR要大才行?
不同類型adc的優缺點
adc的分類及特點
TLV1548 CMOS 10位開關電容逐次逼近型(SAR)模數(A/D)轉換器數據表

ADS9110逐次逼近寄存器(SAR)模數轉換器(ADC)數據表

ADS9120逐次逼近寄存器(SAR)模數轉換器(ADC)數據表

ADS8694和ADS8698基于18位逐次逼近寄存器(SAR)模數轉換器(ADC)數據表

ADS774H一款12位、逐次逼近型模數轉換器(ADC)數據表

ADS868x單電源逐次逼近寄存器(SAR)模數轉換器(ADC)數據表

ADC161S626一款16位逐次逼近型模數轉換器(ADC)數據表

TLV2543C和TLV2543l逐次逼近型模數轉換器(ADC)數據表

ADC08831/ADC08832 8位逐次逼近型模數轉換器數據表

逐次逼近型A/D轉換器的工作原理和特點
模數轉換器:并行比較型和逐次逼近型
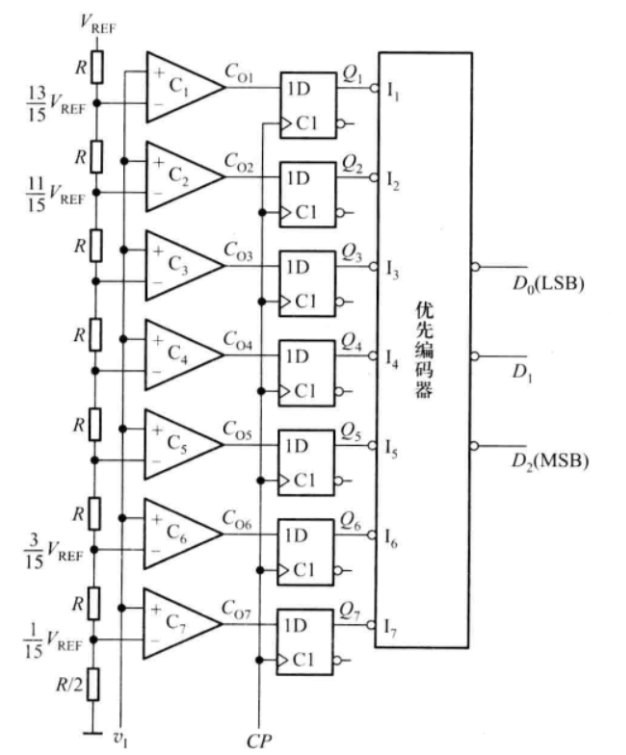




 一個基本的逐次逼近型 ADC 原理框圖解析
一個基本的逐次逼近型 ADC 原理框圖解析










評論