什么是串級PID?
什么是串級PID?顧名思義就是兩個串起來的PID,下面是一個雙閉環的例子,外環是位置環,內環是速度環,最終的執行器是電機,電機輸出產生了速度和位置;具體框圖如下圖所示;
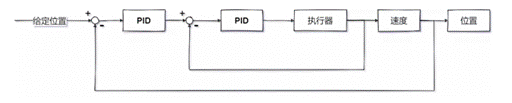
當然執行器也可以是四軸飛行器,整體過程如下:
我們在外環給定相應的位置高度,外環PID的輸出就是內環PID的期望值;
內環PID的輸出將產生相應的油門大小,最終飛行器會產生上升的速度;
內環反饋值為速度,控制相應的速度達到外環所需的速度期望值;
最終外環達到期望的位置;
可能這里比較抽象,好吧,下面繼續細化一下硬件的細節;
PID的算法控制其實是一種無系統模型的控制,可以根據參數經驗經驗去調試系統;
但是實際的物理對象的模型其實早就確定好了,PID的輸入量和輸出量的物理意義也會因為實際的被控對象而改變;
換句話說,PID的輸入基本上和系統的反饋量相關,而實際的反饋量是什么,從一開始就因為系統而確定下來了;
內環和外環
如果外環是因,那內環就是果。萬物皆有因果。
比如伺服控制器的三環:
- 位置環
- 速度環
- 電流環
外環的變化會直接導致內環的變化,而內環是直接導致執行器變化的關鍵,如果這里依然使用飛行器作為例子,對于整個四軸飛行系統而言;
我們通過控制電機的電流,從而決定電機的輸出扭矩;
扭矩和負載一起決定電機轉速;
螺旋槳快速旋轉從而產生了飛行器的升力,于是也決定了上升的速度;
最終也導致了飛行器的位置變化;
這是整個的控制過程。
如果只用單環的PID去控制系統,可以在給定系統期望的情況下達到所需要的位置嗎?
答案是可以。
那這樣串級PID還有什么意義嗎?
答案是有。
我們試想一下,如果單純使用單環PID去控制系統。
那我們看一下單環的PID系統框圖;

我們設定了一個高度,并且希望飛行器達到預期位置高度,那么這時候系統的反饋值只有位置量;
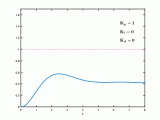
那么飛行器是以什么樣的速度去飛行?以什么樣的加速度去啟動?我們就無法去有效地控制飛行器的速度,讓它去快速地到達期望的位置,具體位置曲線如下圖所示;
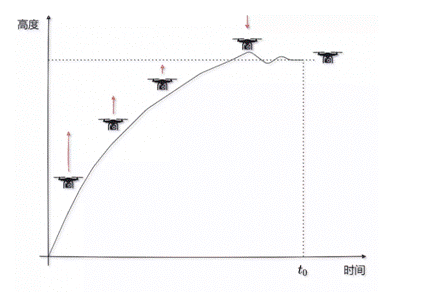
其實不難理解,因為一開始的高度差很大,所以PID計算輸出的值就很大,因此初始速度會非常大,隨著飛行器越來越接近期望位置,偏差越來越小,PID輸出量逐漸減小,因此速度逐漸減小。
其實很多時候,PID只是底層,稱之為內環PID,通過它可以先穩定某個系統,優化動態特性,然后在外層嵌套其他算法,當然,外面有好幾層PID的控制系統是也很常見的。也就是我們介紹的串級PID的系統,具體如下所示;

控制器的本質是出入跟輸出的函數映射關系。
其實從這個角度來看,通常PID適用于低階的線性時不變系統,在此基礎上限制到P,I,D三個系數。
整體還需要根據具體的系統,有所變化,有的系統其實只需要兩個系數(比如PD或PI),甚至有的系統只需要一個就行(比如P)。因此上面系統中,外環只需要使用P環節就足夠了,另外可以對速度曲線進行規劃。
假設這里使用了速度曲線規劃,因為可以對飛行器的速度進行控制了;
所以我們期望它盡快達到最大速度,因此從最開始的階段進行勻加速,達到最大速度后開始勻速上升,即將到達期望位置的時候,進行勻減速,最終懸停到目標位置;
那么整體的位置變化曲線如下所示;
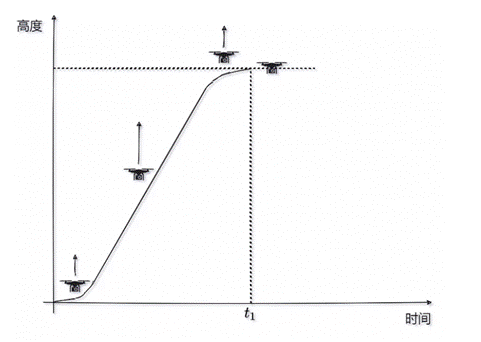
換句說話說,就是外環PID的輸出作為內環PID的輸入;
下面是單環PID的偽算法;
previous_error := 0 //上一次偏差
integral := 0 //積分和
//循環
//采樣周期為dt
loop:
//setpoint 設定值
//measured_value 反饋值
error := setpoint ? measured_value //計算得到偏差
integral := integral + error × dt //計算得到積分累加和
derivative := (error ? previous_error) / dt //計算得到微分
output := Kp × error + Ki × integral + Kd × derivative //計算得到PID輸出
previous_error := error //保存當前偏差為下一次采樣時所需要的歷史偏差
wait(dt) //等待下一次采用
goto loop
那么改成串級PID需要如何操作呢?
具體偽算法如下所示;
previous_error := 0 //上一次偏差
integral := 0 //積分和
previous_error_inner := 0 //內環PID上一次偏差
integral_inner := 0 //內環PID積分和
//循環
//采樣周期為dt
loop:
//外環計算
//setpoint 外環設定值
//measured_value 外環反饋值
error := setpoint ? measured_value //計算得到偏差
integral := integral + error × dt //計算得到積分累加和
derivative := (error ? previous_error) / (n*dt) //計算得到微分
output := Kp × error + Ki × integral + Kd × derivative //計算得到PID輸出
previous_error := error //保存當前偏差為下一次采樣時所需要的歷史偏差
setpoint_inner = output //外環的PID輸出賦值給內環的PID輸入
wait(n*dt) //等待下一次采樣
goto loop
loop_inner:
//setpoint_inner 內環設定值
//measured_value_inner 內環反饋值
error_inner := setpoint_inner ? measured_value_inner //計算得到偏差
integral_inner := integral_inner + error_inner × dt //計算得到積分累加和
derivative_inner := (error_inner ? previous_error_inner) / dt //計算得到微分
//計算得到PID輸出
output_inner := Kp_inner × error + Ki_inner × integral_inner + Kd_inner × derivative_inner
previous_error_inner := error_inner //保存當前偏差為下一次采樣時所需要的歷史偏差
wait(dt) //等待下一次采樣
goto loop_inner
這里將內環PID的相關變量加了后綴 _inner,loop是外環PID進行周期控制,loop_inner是內環PID進行周期控制,兩者相互獨立,將外環PID的輸出賦值給內環PID的輸入即可;
遇到干擾的時候,內環控制器首先進行粗調,外環控制器再進一步細調。
因此控制效果必然優于單環的PID控制系統。
串級控制系統在結構上僅僅比簡單控制系統多了一個內環回路,可是實踐證明,對于相同的干擾,串級控制系統的控制質量是簡單控制系統無法比擬的。
PID參數
串級PID的參數整定基本遵循從內到外,先整定內環PID的參數,再整定外環PID的參數;
根據經驗法調試參數,通常來說先整定內環比例參數P,然后整定積分參數I,動態特性可以整理微分參數D,當然還需要對飽和的情況進行處理;
總之可以觀察輸入輸出曲線;
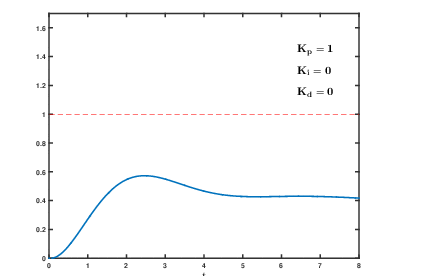
那到底什么樣的響應曲線算好的呢?
一般來說并不存在最優的,比如有的對速度和加速度有限制,有的系統一定不能出現超調量等等,有的系統則是響應越快越好。所以還是那句話,我不要你覺得,我要我覺得,合適才是最好的。
總結
本文簡單介紹了串級PID的相關概念,以四軸飛行器為例,對比了簡單PID和串級PID的優劣;
編輯:hfy
-
PID
+關注
關注
35文章
1473瀏覽量
85648 -
執行器
+關注
關注
5文章
378瀏覽量
19383 -
外環控制器
+關注
關注
0文章
2瀏覽量
5862 -
PID 算法控制
+關注
關注
2文章
2瀏覽量
4894
發布評論請先 登錄
相關推薦
如何使用Python實現PID控制
如何選擇合適的PID控制器
如何調節PID參數 PID控制器的調試方法
什么是PID控制與傳統控制的區別
PID控制的優缺點分析 PID參數調節的常見方法
如何使用PID進行溫度控制
PID算法的基本原理介紹
串級控制系統副回路為什么不選用PID控制
PID控制的原理與作用
PID在工業控制領域的應用
位置式PID與增量式PID的區別
什么是PID?PID各個參數有什么作用?




 什么是串級PID? 簡單PID和串級PID的優劣對比
什么是串級PID? 簡單PID和串級PID的優劣對比










評論