作者說：我以前一直沒有真正理解支持向量機，直到我畫了一張圖。

1. 問題

支持向量機（SVM）旨在解決「分類」問題。數據通常包含一定數量的條目/行/點。現在，我們想對每個數據點進行分類。為簡單起見，我們假設兩個類別：「正類」和「負類」。這或許可以幫助解答以下問題：

基于圖像的像素數據，判斷這張圖像中是否有貓（有貓則標簽為正類）；

基于郵件的主題、發送者、文本等，判斷該郵件是否為垃圾郵件；

判斷某個病人是否患有某種疾病。

其精髓在于，當我們知道正確答案時，我們會想到一些將數據分為兩類的規則（對于支持向量機而言，「規則」是畫一個平面，一側的所有點均為「正」，另一側的所有點均為「負」）。當我們遇到不知道類別的新數據點時，我們使用規則對其進行分類。分類問題嚴重依賴約束優化，同時也是約束優化的一個直觀示例。大家可以參考以下博客或吳恩達的文章。

博客地址：https://towardsdatascience.com/lagrange-multipliers-with-pictures-and-code-ace8018dac5e

吳恩達文章地址：http://cs229.stanford.edu/notes/cs229-notes3.pdf

1.1 圖解

我以前一直沒有真正理解支持向量機，直到我畫了一張圖。

我們可以看到特征空間中有一些點。為方便可視化，我們使用一個可在屏幕上觀看的 2D 特征空間。該空間中散落著一些數據點，每個點具備二元標簽（(1/-1）。如下圖所示，我們將綠色點看作正類，紅色點看作負類，黃色點類別未知。如果讓你猜測黃色點的標簽，你會怎么選？你可能會發現其中一些點并不是那么容易確認類別。

圖 1：2-D 分類問題。綠色點是正類，紅色點是負類。你可以猜出黃色點的標簽嗎？（繪圖工具：https://github.com/ryu577/pyray）

現在，如果我畫一條紫色線將兩個類別分割開，那么黃色點屬于哪個類別就清晰多了（紫色線上方是綠色點，下方是紅色點）。

圖 2：畫一條線，作為將正類標簽和負類標簽分割開來的「規則」。現在，我們可以使用該規則標注每個黃色點的類別。

然而，這條線并非唯一。有很多條紫色線可以將綠色點和紅色點完美分割（見下圖）。隨著下圖中紫色線的移動，某些黃色點就顯得很微妙了（它們處于紫色線的不同側，因此它們的類別取決于你選擇使用哪條紫色線）。

圖 3：將紅色點和綠色點完美分割的線有很多條。那么我們應該選擇哪一條呢？

問題在于，所有候選線中，哪一條是「最優」的？有一點很清楚：當上圖中的紫色線接近右下角的紅色點（critical point）時，其泛化效果不好，而當它遠離那個點時，其分割效果要好得多。因此，這個紅色點可以說明紫色線的分類效果，因此它是「關鍵點」。我們可以說，遠離該紅色點的線同樣遠離所有訓練樣本，而靠近該紅色點的線最終的分類效果并不好。因此，離最近的訓練樣本較遠的線才是優秀的分類器。

接下來，我們來看如何利用數學知識繪制分割線。

2. 繪制分割線

現在我們要（在 2D 空間中）畫一條分割線（在更高維度的空間中，則為分割面）。那么這條線是什么呢？它是具備某種共性的點的無限集合。這些點滿足一個特定公式。為了找到這個公式，我們先從最簡單的線 x 軸開始。x 軸上所有點的位置向量存在什么共性？v_x = [x,0]，即它們對應的 y 坐標均為 0。

也就是說，x 軸上每個點的位置向量與指向 y 軸方向的向量是正交（垂直）的。

這個說法可能看起來比較晦澀難懂，但是我們必須這么說，因為這種現象其實對所有線都成立，而并非只適用于 x 軸。我們希望將此說法泛化至任意線。現在每次挪動一小步，我們來看看穿過原點的線（如 x 軸）。如下圖所示，只需將 x 軸旋轉一定角度，就可以得到這些線。

圖 4：旋轉 x 軸可以得到穿過原點的任意線。這些線上的每個點都與橙色向量相垂直。

隨著線的變化，與線相垂直的向量也在變化，但是所有線上每個點的位置向量都與某個向量垂直。我們把這個與線垂直的向量叫做 w。當我們改變 w 時，就可以捕捉到所有此類線。

注意，對于任意給定線而言，存在多個 w 值。如果我們將向量 w 擴展或縮小一定數值，該線上每個點的位置向量仍與向量 w 垂直。

圖 5：擴大或縮小正交 w 向量。

為什么不把 w 向量限制在大小為 1 呢？下文中，我們將 w 向量的大小設為 1。

現在我們已經將穿過原點的所有線都參數化了。那么那些沒有穿過原點的線呢？我們將穿過原點的線移動一定量，即在該線法向量 w 的方向上移動 b。現在，w 與該線上每個點的位置向量的點積不為零，而是常量 b（參見下圖）。w 向量是從原點指向紫色線的單位向量，且與紫色線垂直。A 即紫色線上與原點最接近的點。假設 OA 的距離是 -b。現在，考慮兩個隨機點 B 和 C（分別是圖中綠色點和橙色點）。將 OB 或 OC 與單位向量 w 相乘，分別得到三角形 OAB 和 OAC 的底。 在這兩種情況中，OA 為 -b。由于這兩個點只是紫色線上的任意點，我們可以推斷出，紫色線上的所有點均滿足 w^T x+b=0（其中 x 表示紫色線上點的位置向量）。

圖 6：未穿過原點的線。

如果我們將不在該線上的點應用于上述公式呢？得到的結果不是零，而是從該點到紫色線的垂直距離（對于紫色線上的點而言也是如此，所以它們所對應的公式結果為零）。我們需要注意：這個結論僅適用于 |w|=1 的情況。下圖清晰說明了這一結果。B 為不屬于紫色線的任意點，B』』 為從 B 到紫色線的垂點，B』 為從 B 到 w 向量的垂點。從 B 到紫色線的垂直距離為 BB』』。但是由于 A-B』-B-B』』 是一個矩形，因此該垂直距離等于 AB』=OB』-OA。現在，OB』 是 B 的位置向量與 w 的點積。因此，如果 x 是 B 的位置向量，則 |OB』| = w^T x。這意味著 |AB』|=w^T x-(-b)（OA=-b）。因此從點 B 到紫色線的距離是：|AB』|=w^T x+b（該公式恰好是紫色線的公式）。

圖 7：將不在紫色線上的點應用于紫色線公式會發生什么？我們得到該點與紫色線之間的垂直距離。

注意，在 w 指向方向一側的所有點（如圖 7 中的點 B）到紫色線的垂直距離為正值，而另一側點的垂直距離為負值。

在 w 指向方向一側的所有點均得到正類標簽 (t_i=1)，而另一側的所有點均得到負類標簽 (t_i=-1)。因此，如果我們將這些標簽與垂直距離相乘，則所有點調整后的垂直距離均為正，前提是這些點均被紫色線正確分類（即具備正類標簽的點在線一側，具備負類標簽的點在另一側）。

3. 最佳分割線

現在到了 SVM 的重點了。我們將任意點到分割線的調整后垂直距離叫做「間距」（margin）。那么，對于任意給定分割線，所有點均具備間距（如果點被分割線正確分類，則間距為正，反之則間距為負）。我們想獲取將正類和負類完美分割的線。也就是說，間距越大越好，即使是對于鄰近界限（分割平面）的點。

那么，最大化所有間距（甚至是最接近分割線的點的間距）的分割平面應該能夠很好地分割這些點。現在，給出 (w,b)，第 i 個點的間距為：

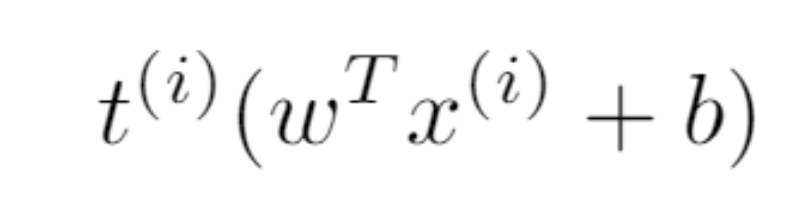
間距公式。

其中 x_i 表示特征空間中的位置向量，t_i 表示標簽：1 為正類，-1 為負類。

所有點中的最小間距為：

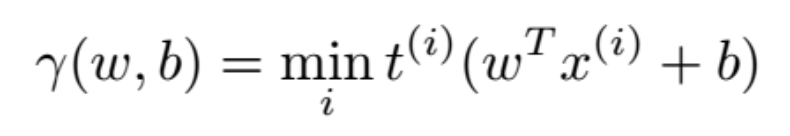
公式 1：所有點中的最小間距。

我們想讓 (w,b) 最大化上述最小間距。也就是：

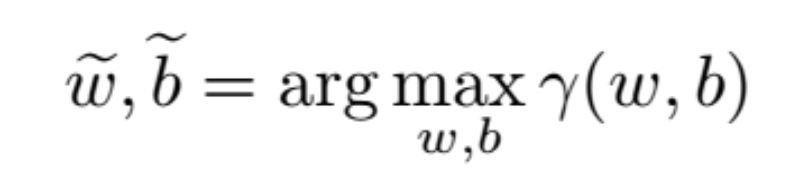
即我們想讓 (w,b) 滿足 |w|=1，且最大化間距：

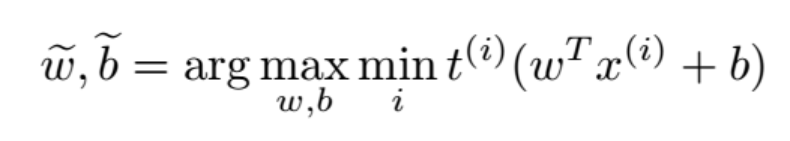
公式 2：SVM 目標函數。

注意：如果這條線沒有分離數據，那么對于 (w,b)，某些點的間距

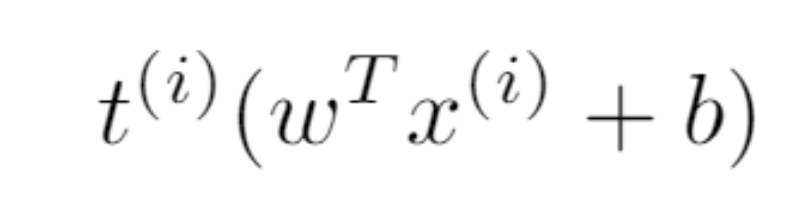
間距公式。

為負。且這些點中的其中一個會在第一次最小化中「脫穎而出」，這意味著 (w,b) 無法在第二次 arg max 時勝出。因此，該公式保證了勝出的 (w,b) 能夠分割數據。

公式 2 是一個優化問題，涉及最小化和最大化（mini-max）。解決一級優化總比二級優化要簡單。因此，我們嘗試將公式 2 轉化為約束優化問題。

我們用 γ 表示所有點的最小間距。

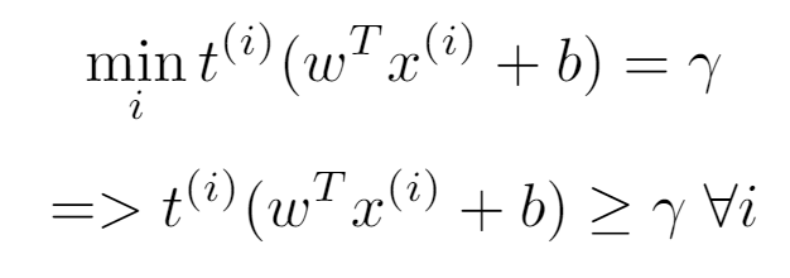
公式 3：約束。

最終得到的優化問題為：

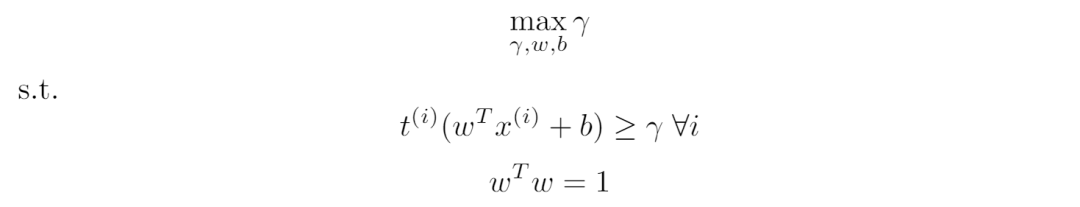
公式 4：SVM 優化問題。

上述優化問題具備二次/線性約束和線性目標函數。我們可以使用二次規劃求解器（quadratic programming solver）和最優分割線/平面 (w,b) 解決該問題。

現在，我們來試著進一步簡化該問題。我們發現可以去除 γ。其代價是，我們必須放棄 w^T w = 1 這一要求。但這是值得的。我們使用 γ 將約束分割為兩部分，得到：

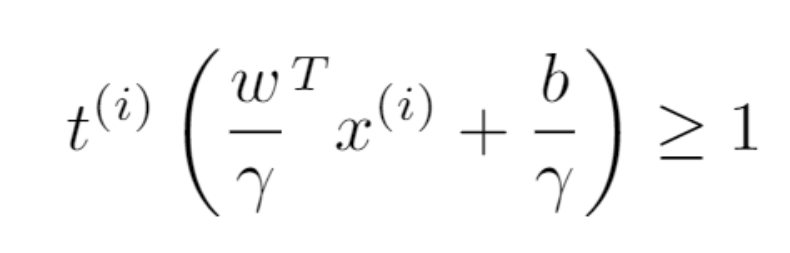
公式 5：使用 γ 分割分割平面公式。

現在，使

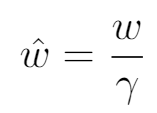
引入新的 w 變量。

為兩側取絕對值：

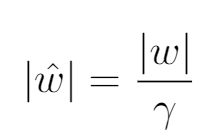
取絕對值。

我們之前要求 |w|=1。這意味著：

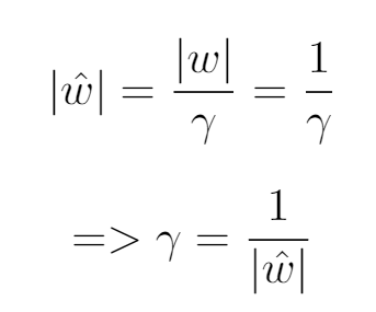
因此，公式 3 變成了：

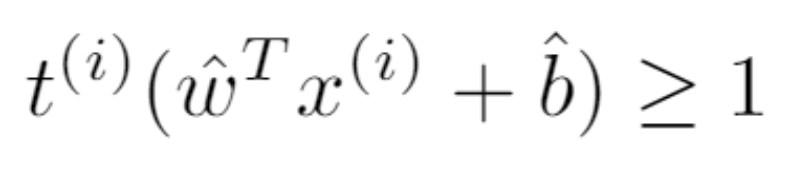
公式 5 和公式 6 使公式 4 中的優化問題變成了：

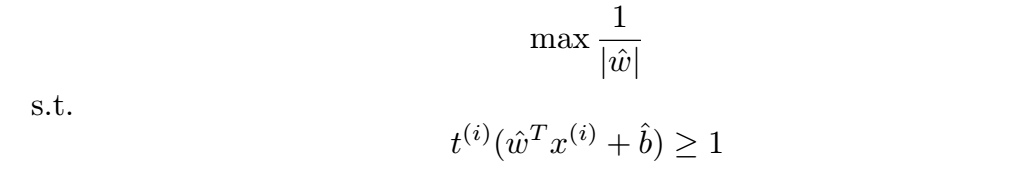
現在，優化問題有了一個丑陋的目標函數。但是最大化 1/|w| 等同于最小化 |w|，等同于最小化 |w|2。添加 1/2 使得計算更加簡單。

因此，上述優化問題變為：

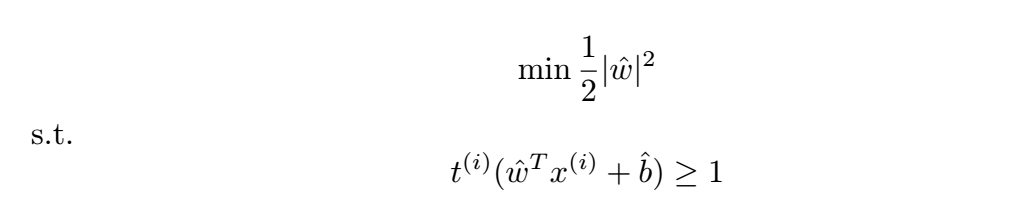
公式 7

現在，該優化問題具備二次目標函數和線性約束（線性約束二次規劃，LCQP）。使用二次規劃求解器即可解決該問題。

現在，我們知道如何通過解決優化問題找出最優分割線了。透過表面查看解決這類優化問題的真正機制，會幫助我們對該問題了解更多，具備更強大的洞察和見解。

責任編輯：xj

原文標題：透過現象看本質，圖解支持向量機 SVM

文章出處：【微信公眾號：新機器視覺】歡迎添加關注！文章轉載請注明出處。