今天講一道非常有意思,而且比較有難度的題目。
我們知道一個矩形有四個頂點,但是只要兩個頂點的坐標就可以確定一個矩形了(比如左下角和右上角兩個頂點坐標)。
來看看力扣第 391 題「完美矩形」,題目會給我們輸入一個數組rectangles,里面裝著若干四元組(x1,y1,x2,y2),每個四元組就是記錄一個矩形的左下角和右上角頂點坐標。
也就是說,輸入的rectangles數組實際上就是很多小矩形,題目要求我們輸出一個布爾值,判斷這些小矩形能否構成一個「完美矩形」。函數簽名如下:
defisRectangleCover(rectangles:List[List[int]])->bool
所謂「完美矩形」,就是說rectangles中的小矩形拼成圖形必須是一個大矩形,且大矩形中不能有重疊和空缺。
比如說題目給我們舉了幾個例子:

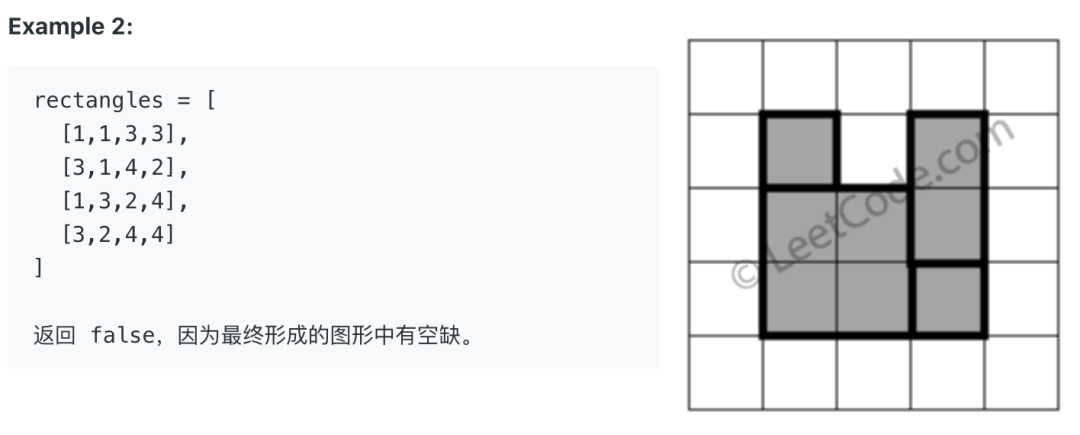

這個題目難度是 Hard,如果沒有做過類似的題目,還真做不出來。
常規的思路,起碼要把最終形成的圖形表示出來吧,而且你要有方法去判斷兩個矩形是否有重疊,是否有空隙,雖然可以做到,不過感覺異常復雜。
其實,想判斷最終形成的圖形是否是完美矩形,需要從「面積」和「頂點」兩個角度來處理。
先說說什么叫從「面積」的角度。
rectangles數組中每個元素都是一個四元組(x1, y1, x2, y2),表示一個小矩形的左下角頂點坐標和右上角頂點坐標。
那么假設這些小矩形最終形成了一個「完美矩形」,你會不會求這個完美矩形的左下角頂點坐標(X1, Y1)和右上角頂點的坐標(X2, Y2)?
這個很簡單吧,左下角頂點(X1, Y1)就是rectangles中所有小矩形中最靠左下角的那個小矩形的左下角頂點;右上角頂點(X2, Y2)就是所有小矩形中最靠右上角的那個小矩形的右上角頂點。
注意我們用小寫字母表示小矩形的坐標,大寫字母表示最終形成的完美矩形的坐標,可以這樣寫代碼:
#左下角頂點,初始化為正無窮,以便記錄最小值
X1,Y1=float('inf'),float('inf')
#右上角頂點,初始化為負無窮,以便記錄最大值
X2,Y2=-float('inf'),-float('inf')
forx1,y1,x2,y2inrectangles:
#取小矩形左下角頂點的最小值
X1,Y1=min(X1,x1),min(Y1,y1)
#取小矩形右上角頂點的最大值
X2,Y2=max(X2,x2),max(Y2,y2)
這樣就能求出完美矩形的左下角頂點坐標(X1, Y1)和右上角頂點的坐標(X2, Y2)了。
計算出的X1,Y1,X2,Y2坐標是完美矩形的「理論坐標」,如果所有小矩形的面積之和不等于這個完美矩形的理論面積,那么說明最終形成的圖形肯定存在空缺或者重疊,肯定不是完美矩形。
代碼可以進一步:
defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')
#記錄所有小矩形的面積之和
actual_area=0
forx1,y1,x2,y2inrectangles:
#計算完美矩形的理論坐標
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)
#累加所有小矩形的面積
actual_area+=(x2-x1)*(y2-y1)
#計算完美矩形的理論面積
expected_area=(X2-X1)*(Y2-Y1)
#面積應該相同
ifactual_area!=expected_area:
returnFalse
returnTrue
這樣,「面積」這個維度就完成了,思路其實不難,無非就是假設最終形成的圖形是個完美矩形,然后比較面積是否相等,如果不相等的話說明最終形成的圖形一定存在空缺或者重疊部分,不是完美矩形。
但是反過來說,如果面積相同,是否可以證明最終形成的圖形是完美矩形,一定不存在空缺或者重疊?
肯定是不行的,舉個很簡單的例子,你假想一個完美矩形,然后我在它中間挖掉一個小矩形,把這個小矩形向下平移一個單位。這樣小矩形的面積之和沒變,但是原來的完美矩形中就空缺了一部分,也重疊了一部分,已經不是完美矩形了。
綜上,即便面積相同,并不能完全保證不存在空缺或者重疊,所以我們需要從「頂點」的維度來輔助判斷。
記得小學的時候有一道智力題,給你一個矩形,切一刀,剩下的圖形有幾個頂點?答案是,如果沿著對角線切,就剩 3 個頂點;如果橫著或者豎著切,剩 4 個頂點;如果只切掉一個小角,那么會出現 5 個頂點。
回到這道題,我們接下來的分析也有那么一點智力題的味道。
顯然,完美矩形一定只有四個頂點。矩形嘛,按理說應該有四個頂點,如果存在空缺或者重疊的話,肯定不是四個頂點,比如說題目的這兩個例子就有不止 4 個頂點:
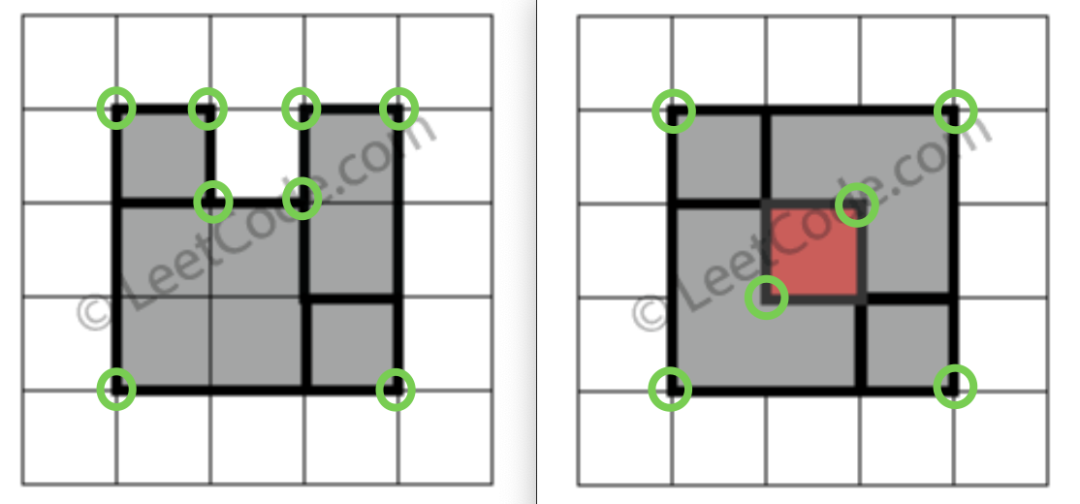
PS:我也不知道應該用「頂點」還是「角」來形容,好像都不太準確,本文統一用「頂點」來形容,大家理解就好~
只要我們想辦法計算rectangles中的小矩形最終形成的圖形有幾個頂點,就能判斷最終的圖形是不是一個完美矩形了。
那么頂點是如何形成的呢?我們倒是一眼就可以看出來頂點在哪里,問題是如何讓計算機,讓算法知道某一個點是不是頂點呢?這也是本題的難點所在。
看下圖的四種情況:
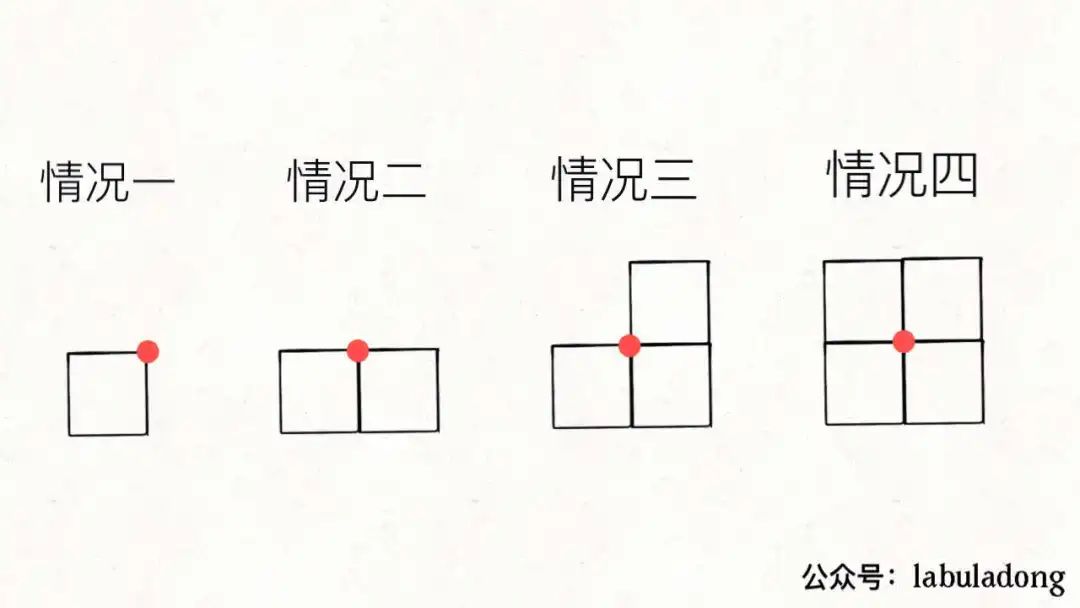
圖中畫紅點的地方,什么時候是頂點,什么時候不是頂點?顯然,情況一和情況三的時候是頂點,而情況二和情況四的時候不是頂點。
也就是說,當某一個點同時是 2 個或者 4 個小矩形的頂點時,該點最終不是頂點;當某一個點同時是 1 個或者 3 個小矩形的頂點時,該點最終是一個頂點。
注意,2 和 4 都是偶數,1 和 3 都是奇數,我們想計算最終形成的圖形中有幾個頂點,也就是要篩選出那些出現了奇數次的頂點,可以這樣寫代碼:
defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')
actual_area=0
#哈希集合,記錄最終圖形的頂點
points=set()
forx1,y1,x2,y2inrectangles:
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)
actual_area+=(x2-x1)*(y2-y1)
#先算出小矩形每個點的坐標
p1,p2=(x1,y1),(x1,y2)
p3,p4=(x2,y1),(x2,y2)
#對于每個點,如果存在集合中,刪除它;
#如果不存在集合中,添加它;
#在集合中剩下的點都是出現奇數次的點
forpin[p1,p2,p3,p4]:
ifpinpoints:points.remove(p)
else:points.add(p)
expected_area=(X2-X1)*(Y2-Y1)
ifactual_area!=expected_area:
returnFalse
returnTrue
這段代碼中,我們用一個points集合記錄rectangles中小矩形組成的最終圖形的頂點坐標,關鍵邏輯在于如何向points中添加坐標:
如果某一個頂點p存在于集合points中,則將它刪除;如果不存在于集合points中,則將它插入。
這個簡單的邏輯,讓points集合最終只會留下那些出現了 1 次或者 3 次的頂點,那些出現了 2 次或者 4 次的頂點都被消掉了。
那么首先想到,points集合中最后應該只有 4 個頂點對吧,如果len(points) != 4說明最終構成的圖形肯定不是完美矩形。
但是如果len(points) == 4是否能說明最終構成的圖形肯定是完美矩形呢?也不行,因為題目并沒有說rectangles中的小矩形不存在重復,比如下面這種情況:
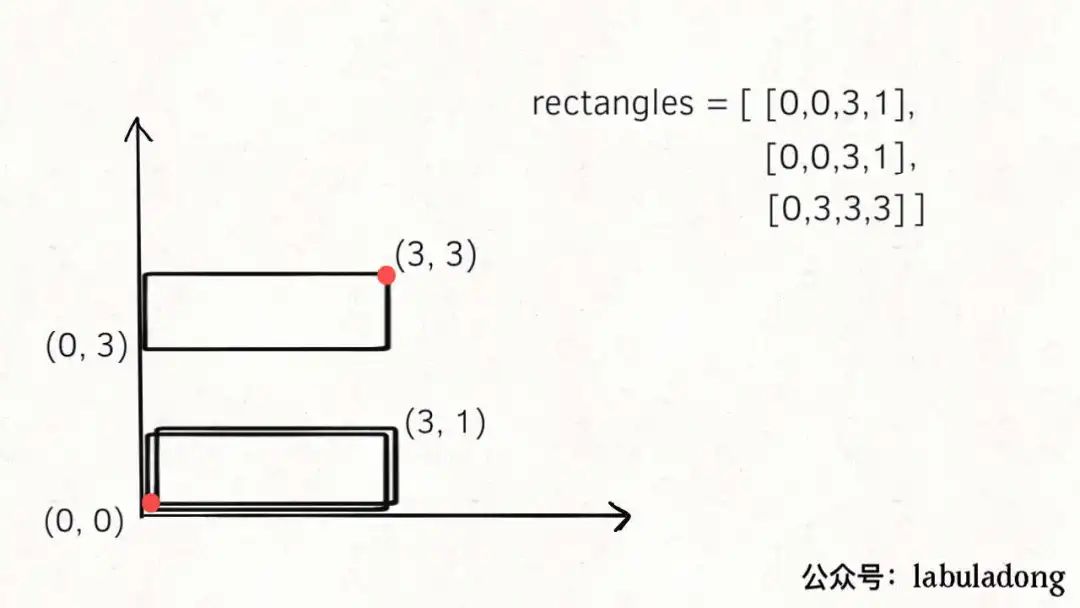
下面兩個矩形重復了,按照我們的算法邏輯,它們的頂點都被消掉了,最終是剩下了四個頂點;再看面積,完美矩形的理論坐標是圖中紅色的點,計算出的理論面積和實際面積也相同。但是顯然這種情況不是題目要求完美矩形。
所以不僅要保證len(points) == 4,而且要保證points中最終剩下的點坐標就是完美矩形的四個理論坐標,直接看代碼吧:
defisRectangleCover(rectangles:List[List[int]])->bool:
X1,Y1=float('inf'),float('inf')
X2,Y2=-float('inf'),-float('inf')
points=set()
actual_area=0
forx1,y1,x2,y2inrectangles:
#計算完美矩形的理論頂點坐標
X1,Y1=min(X1,x1),min(Y1,y1)
X2,Y2=max(X2,x2),max(Y2,y2)
#累加小矩形的面積
actual_area+=(x2-x1)*(y2-y1)
#記錄最終形成的圖形中的頂點
p1,p2=(x1,y1),(x1,y2)
p3,p4=(x2,y1),(x2,y2)
forpin[p1,p2,p3,p4]:
ifpinpoints:points.remove(p)
else:points.add(p)
#判斷面積是否相同
expected_area=(X2-X1)*(Y2-Y1)
ifactual_area!=expected_area:
returnFalse
#判斷最終留下的頂點個數是否為4
iflen(points)!=4:returnFalse
#判斷留下的4個頂點是否是完美矩形的頂點
if(X1,Y1)notinpoints:returnFalse
if(X1,Y2)notinpoints:returnFalse
if(X2,Y1)notinpoints:returnFalse
if(X2,Y2)notinpoints:returnFalse
#面積和頂點都對應,說明矩形符合題意
returnTrue
這就是最終的解法代碼,從「面積」和「頂點」兩個維度來判斷:
1、判斷面積,通過完美矩形的理論坐標計算出一個理論面積,然后和rectangles中小矩形的實際面積和做對比。
2、判斷頂點,points集合中應該只剩下 4 個頂點且剩下的頂點必須都是完美矩形的理論頂點。
說實話,如果沒做過,這種特性真不是一時半會能想到的,但是看過一遍沒問題了,你學會了嗎?
責任編輯:xj
原文標題:這道「完美矩形」給我整不會了…
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
-
函數
+關注
關注
3文章
4338瀏覽量
62738 -
代碼
+關注
關注
30文章
4801瀏覽量
68734
原文標題:這道「完美矩形」給我整不會了…
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
為什么選擇日晟萬欣矩形連接器?

硬件工程師面試常考的一道題,講講運算放大器的增益帶寬積

ADS131E08輸入信號后都疊加在矩形波上,為什么?
【「大話芯片制造」閱讀體驗】+跟著本書”參觀“半導體工廠
ADS1256 8通道依次采樣,數據不正確怎么解決?
企業如何數字化轉型
Verilog testbench問題求助
遲滯比較器和滯回比較器是一樣的嗎
一種新的微帶線和矩形波導集成形結構研究




 一道比較有難度的完美矩形題
一道比較有難度的完美矩形題













評論