有同學在學習圖論算法的時候，發現這里有個 Tarjan 算法，那里有個 Tarjan 算法，而似乎 Tarjan 算法解決的問題并不一樣，于是非常迷惑：Tarjan 算法到底是指什么？

這是一個很好的問題。Tarjan 是計算機領域的大牛，發明了很多現在大家耳熟能詳的算法或者數據結構，所以有同學會覺得冠他名字的算法有些多。

但如果我們仔細梳理一下，其實并不復雜。

在這篇文章中，我會帶領大家梳理一下 Tarjan 發明的算法都有哪些，整體脈絡是怎樣的。

注意：在這篇文章中，我不會具體講解某個算法的原理。但是，我會給出很多具體的關鍵字，并且標紅。如果大家對某個算法想深入了解，可以以此為引，在互聯網上搜索學習。

我相信，互聯網上關于某個具體算法的資料是非常多的，反而是這樣按照某個脈絡做總結的文章很少。

首先，Tarjan 是一名美國的計算機科學家和數學家，全名 Robert Endre Tarjan。

先來一個 Tarjan 大神的名言鎮樓：

一般提起 Tarjan 算法，通常是指 Tarjan 發明的求解有向圖的強聯通分量算法，全稱是Tarjan’s Strongly Connected Components Algorithm.

為什么這么叫？因為求解有向圖的強聯通分量還有一個著名算法：Kosaraju 算法。Kosaraju 算法也是以他的發明者的名字命名的。

我在算法比賽中，或者需要求解 SCC（強連通分量的縮寫：Strongly Connected Components） 問題的時候，喜歡寫 Kosaraju 算法。因為 Kosaraju 算法的實現非常簡單，復雜度和 Tarjan 算法是一樣的，都是 O(V + E) 的。

但實際上，Kosaraju 算法需要遍歷兩次圖，而 Tarjan 算法只需要遍歷一次圖。所以，Tarjan 算法的性能更高，一般可以高 30% - 40% 左右。

而 Tarjan 算法之所以有名，關鍵在于使用 Tarjan 算法的思想，不僅僅可以求解 SCC 問題，還可以求無向圖中的橋或者割點。

這就是為什么，很多同學看到 Tarjan 算法，做的事情不一樣，但都叫 Tarjan 算法的原因。我們可以把 Tarjan 算法理解成是一種思想，基于這種思想，可以求解橋，割點，和 SCC 問題。

所謂的 Tarjan 算法思想，就是在遍歷整個圖的過程中，對每一個遍歷的節點記錄一個時間戳，通常被稱為是 DFN；同時，記錄通過這個節點，不經過父親節點，最早能回到的時間戳，通常被稱為是 LOW。通過這些信息，就能判斷一個圖的橋，割點，和強連通分量。

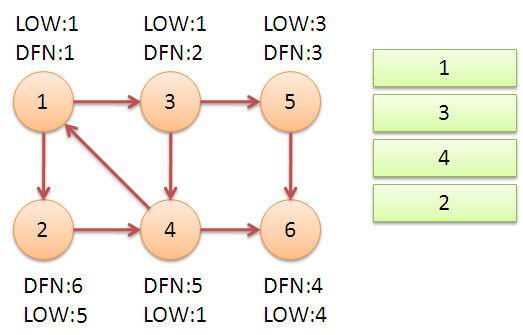
然而，Tarjan 的貢獻遠不止于此。以Tarjan命名的另外一個非常著名的算法，叫Tarjan‘s Off-line Least Common Ancestors Algorithm。

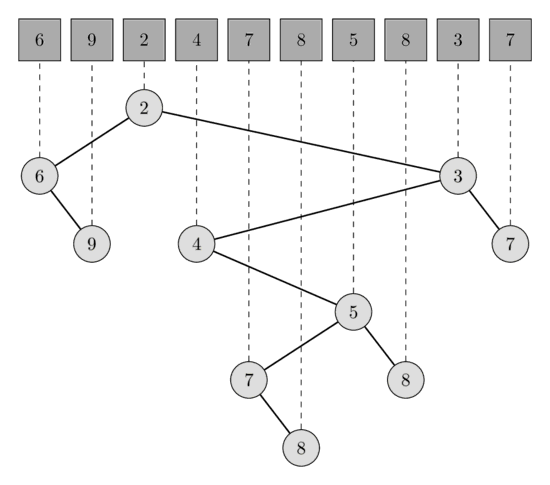
這個算法本質是借助并查集，求解 LCA（最近公共祖先的縮寫：Least Common Ancestors）問題。

實際上，離線的 LCA 問題，是計算機科學領域非常著名的問題，深究下去，和Binary Lifting，RMQ等非常著名的算法思想都有聯系。

說到并查集，Tarjan 也和這種數據結構有不解之緣。并查集雖然不是 Tarjan 發明的，但是并查集的復雜度是 Tarjan 首先分析清楚的：也就是Ackerman 函數的反函數。

如果對此感興趣的同學，可以翻看《算法導論》，《算法導論》對這部分內容介紹得很清楚。

實際上，這也是《算法導論》這本教材的意義：稍微深入一些的算法分析問題，一般的算法教材都不會涉及。而《算法導論》所覆蓋的深度和廣度，比大多數教材都高太多。

當然，這也是《算法導論》不適合入門的原因。

說到數據結構，Tarjan 確實發明過數據結構。最有名的兩個，一個是斐波那契堆，一個是Splay 樹。

Splay 樹雖然不保證一定平衡，但各個操作的均攤復雜度是 O(logn) 級別的。

Splay 樹最大的優勢是實現簡單，比紅黑樹簡單不知道多少倍。所以，如果我們需要調用更加底層的樹操作，需要自己實現一個自平衡的二分搜索樹時，通常 Splay 樹是首選。

也正因為如此，很多搞競賽的同學，都是能手寫 Splay 樹的。

Tarjan 還是非常著名的算法：BFPRT的作者之一。其實 BFPRT 這個算法的名字，是其五個作者首字母的縮寫。其中的 T，就是 Tarjan。

BFPRT 這個名字聽起來非常拗口，同時也難記，但是它的另一個名字就很簡單直接了，就是Median of Medians。

這個算法整體并不難理解，是快排思想的一種更穩定的優化，每次近乎可以保證選取所處理的數組的中位數作為標定點（pivot），使得快速排序的最差時間復雜度真真正正達到了 O(nlogn)。

值得一提的是，BFPRT 算法的這五位作者，都是計算機科學領域的大牛。他們分別是：

B是 Blum，全名 Manuel Blum，他因為復雜度理論方面的貢獻，以及密碼學的應用，獲得了 1995 年的圖靈獎；

F是 Floyd，全名 Robert W. Floyd，相信大家都很熟悉。大家在算法課本上一定會學到的所有點對的最短路徑算法，就是他和 Warshall 一起提出的，即Floyd–Warshall 算法。同時，Floyed 還提出了非常著名的Floyed 環檢測算法。他獲得了 1978 年的圖靈獎；

P是 Pratt，全名 Vaughan Pratt，是斯坦福的教授；

R是 Rivest，全名 Ron Rivest。他是 MIT 的教授，專攻密碼學。我們現在所經常使用的MD5 算法，他就是作者之一；

最后的T，就是這篇文章的主角：Tarjan，全名 Robert Endre Tarjan。

在圖論領域，Tarjan 還改進了一個非常著名的算法：最小樹形圖。最小樹形圖這個名字聽起來很復雜，但其實這個概念很簡單：就是有向圖的最小生成樹。

解決最小樹形圖問題，有一個非常樸素的算法，叫朱劉算法。聽這個名字大家也知道，這是兩位華人科學家首先提出來的算法，在論文記載中，分別是 Y.J. Chu 和 T.H. Liu 在 1965 年提出來的。朱劉算法的時間復雜度是 O(VE) 的。

后來，Tarjan 改進了這個算法，可以使用 O(ElogV) 的時間做預處理，之后使用 O(V) 的時間，求解圖中以任意頂點為根的最小樹形圖

Tarjan 還發明了一種平面圖的檢測算法，首次在線性時間解決了平面圖檢測問題（Planarity-Testing）。因為平面圖檢測離大多數同學的工作比較遠，所以可能很少有同學了解這個算法。

Tarjan 的平面圖檢測算法還有一個合作者：John Hopcroft。他們二人因為這個算法，以及在算法和數據結構等基礎領域對計算機科學的貢獻，獲得了 1986 年的圖靈獎。

Tarjan 的碩士和博士是在斯坦福大學讀的。他的導師有兩個。一個就是大名鼎鼎的 Floyd，上文介紹 BFPRT 算法的時候介紹了。在這里給一個年輕的時候，Floyd 風流倜儻的帥照：

Tarjan 的另一名導師，則是計算機科學領域的神級人物：Donald Knuth。他可以說是計算復雜領域的創始人。

Donald Knuth 的經歷和貢獻，可以寫一本書了。有時間，我會再寫一篇文章介紹他。現在，很多人了解他，都是因為他的神作：TAOCP，即The Art of Computer Programming，被中文翻譯成《計算機程序設計藝術》。這套書被評為至今計算機科學史上最重要的神作，但其實還沒有寫完。

不過 Donald Knuth 對計算機科學領域的貢獻，遠不止一套書這么簡單。要聊 Donald Knuth 的話，能聊的就太多。這篇文章我們收一收，說回 Tarjan。

Tarjan 現在還在世，今年已經 72 歲了。根據維基百科，現在 Tarjan 在普林斯頓任教。

實際上，在計算機科學領域，很多在教科書中出現的人物，都還在世；很多教科書級別的算法，概念，理論，其實距離提出，也不過是幾十年的時間。

這足以可見：計算機是多么年輕的一個學科。

也正是因為這個原因，在計算機科學領域中，還有大量的沒有被完全解決的問題。

計算機科學領域其實還大有可為。

責任編輯：xj

原文標題：Tarjan 這個算法大神

文章出處：【微信公眾號：算法與數據結構】歡迎添加關注！文章轉載請注明出處。