?-Δ 型模數轉換器廣泛用于需要高信號完整度和電氣隔離的電機驅動應用。雖然Σ-Δ技術本身已廣為人知,但轉換器使用常常存在不足,無法釋放這種技術的全部潛力。本文從應用角度考察Σ-Δ ADC,并討論如何在電機驅動中實現最佳性能。
在三相電機驅動中測量隔離相電流時,有多種技術可供選擇。圖1顯示了三種常用方法:一是隔離傳感器(如霍爾效應或電流互感器)結合一個放大器;二是電阻分流器結合一個隔離放大器;三是電阻分流器結合一個隔離Σ-Δ ADC。
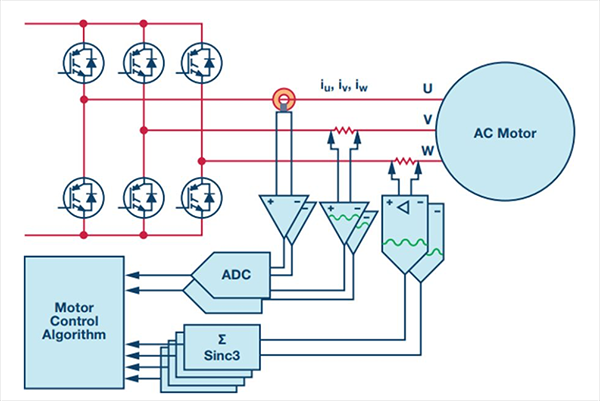
圖1. 三相電機驅動的常見電流測量技術
本文重點討論性能最高的方法——Σ-Δ轉換。通常,Σ-Δ ADC針對的是需要高信號質量和電流隔離度的變頻電機驅動和伺服應用。隨ADC而來的還有解調和濾波,這些一般是由FIR濾波器(如三階sinc濾波器sinc3)處理。
Σ-Δ ADC具有最低的分辨率(1位),但通過過采樣、噪聲整形、數字濾波和抽取,可以實現非常高的信號質量。Σ-Δ ADC和sinc濾波器的原理已廣為人知且有據可查,本文不予討論。本文關注的是如何在電機驅動中實現最佳性能,以及如何在控制算法中利用該性能。
利用Σ-Δ ADC測量相電流
當三相電機由開關電壓源逆變器供電時,相電流可以看作由兩個分量組成:平均分量和開關分量,如圖2所示。最上面的信號為一個相電流,中間的信號為逆變器相位臂的高端PWM,最下面的信號為來自PWM定時器的樣本同步信號PWM_SYNC。PWM_SYNC在PWM周期開始時和中心處置位,因此,它與電流和電壓紋波波形的中點對齊。為簡明起見,假設所有三相的占空比都是50%,意味著電流只有一個上升斜坡和一個下降斜坡。
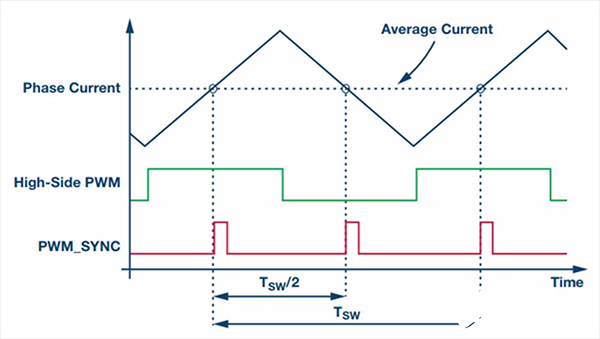
圖2. 相電流在PWM周期開始時和中心處等于平均值
為了控制目的,僅關注電流的平均分量。要提取平均分量,最常見的方法是對與PWM_SYNC同步的信號進行采樣。在此情況下,電流為平均值,因此,如果能對采樣時刻進行嚴格控制,就可以實現欠采樣而不會發生混疊。
使用常規逐次逼近型(SAR) ADC時,采樣由專用采樣保持電路執行,用戶得以嚴格控制采樣時刻。然而,Σ-Δ轉換是一個連續采樣過程,需要通過其它方式來提取電流平均值。為了更好地了解這個問題,看一下Σ-Δ信號鏈的高級視圖會有幫助,如圖3所示。
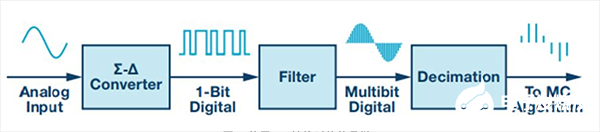
圖3. 使用Σ-Δ轉換時的信號鏈
第一個元件是轉換器本身。以數MHz的速率對模擬信號進行采樣,將其轉換為1位數據流。此外,轉換器對量化噪聲進行整形,將其推到更高頻率。轉換器之后是通過濾波和抽取方式執行的解調。濾波器將1位信號轉換為多位信號,抽取過程將更新速率降低,使之與控制算法相匹配。濾波和抽取可以分兩級完成,但極常見的方法是使用一個sinc濾波器,它能在一級中完成這兩個任務。sinc濾波器可以在FPGA中實現,或者也可以是微處理器中的標準外設(這已是司空見慣)。無論sinc濾波器如何實現,三階(sinc3)是最流行的形式。
從控制方面來說,可以將ADC視作理想器件,通常10MHz到20MHz的轉換速率在數kHz帶寬的控制環路中引入的延遲微不足道。然而,sinc3濾波器會引入一個延遲,使得我們無法談論某個規定的采樣時刻。為了更好地理解這一點,濾波器的復數頻率域表示G(z)會有幫助:
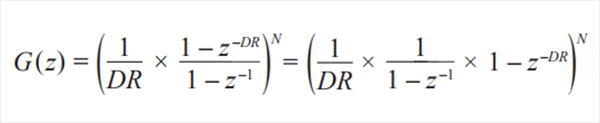
DR為抽取率,N為階數。濾波器為以采樣頻率更新的N個積分器 (1/(1 – z–1))和以抽取頻率(采樣頻率/DR)更新的N個微分器(1 – z–DR)。該濾波器有存儲器,這意味著電流輸出不僅取決于電流輸入,同時也取決于以前的輸入和輸出。通過繪制濾波器脈沖響應曲線可以很好地說明濾波器的這種特性:
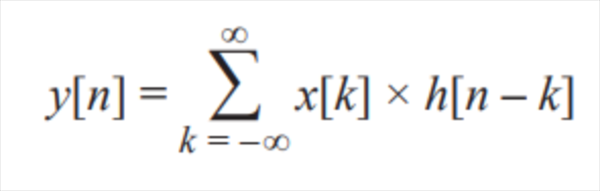
其中,y為輸出序列,x為輸入序列,h為系統脈沖響應。sinc濾波器是一個線性且不隨時間變化的系統,因此脈沖響應h[n]可用來確定任何時間對任何輸入的響應。舉個例子,圖4顯示了一個抽取率為5的三階sinc濾波器的脈沖響應。
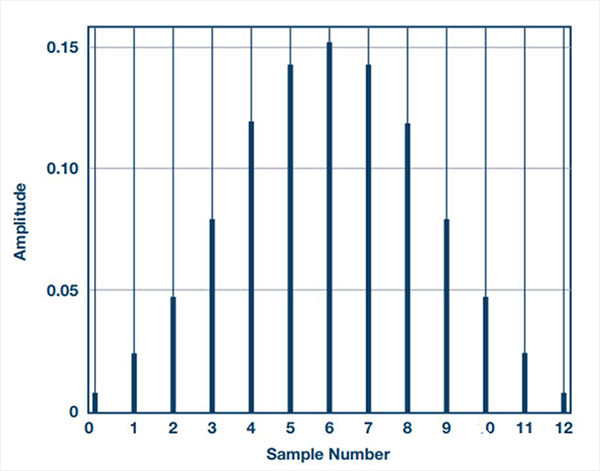
圖4. 三階sinc3濾波器(抽取率為5)的脈沖響應
可以看出,濾波器為加權和,中間的采樣獲得較大權重,而序列開始/結束時的采樣權重較低。由于相電流的開關分量,這一點是必須考慮的,否則反饋會發生混疊。幸運的是,該脈沖響應是對稱的,因此sinc濾波器會賦予中間軸之前和之后的采樣以相同的權重。另外,相電流的開關分量也是對稱的,中心點為平均電流。也就是說,如果在平均電流時刻之前采集了x個等距樣本,并將其加到在平均電流時刻之后采集的x個等距樣本之上,開關分量之和便是0。這可以通過對齊PWM_SYNC脈沖的脈沖響應中心軸來實現,如圖5所示。
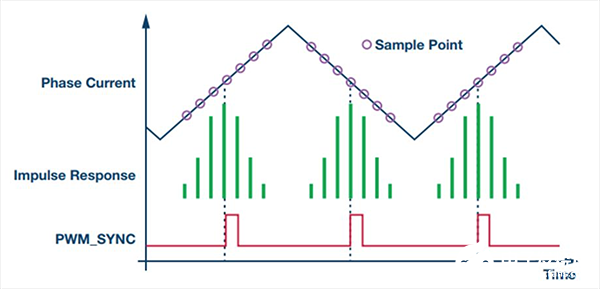
圖5. 對齊sinc濾波器對PWM的脈沖響應
為了正確對齊PWM脈沖響應,必須知道脈沖響應的長度。三階濾波器的脈沖響應中的軸數為:
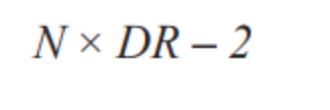
利用此式可以算出以秒為單位的脈沖響應長度:
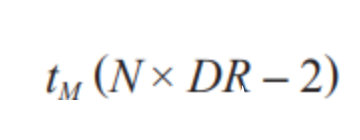
其中,tM為調制器時鐘周期。該時間值很重要,因為它告訴我們一個樣本完全通過濾波器需要多長時間。脈沖響應的中心軸恰好位于總濾波器長度的一半處,因此,一個樣本走完一半路程所需的時間必定為:
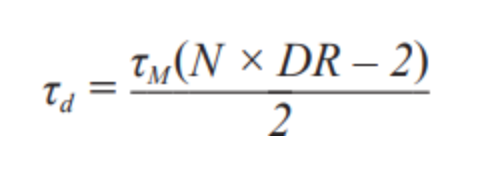
所以,如果輸入采樣開始于PWM_SYNC之前的τd,并且在PWM_SYNC之后的τd讀取濾波器數據,則對齊就會如圖5所示。采樣開始由調制器時鐘的使能/禁用來控制。一旦使能,濾波器就會與PWM保持同步,無需再對齊。
控制時序
通過對齊PWM_SYNC脈沖響應,便可測量相電流而不會有混疊,但在讀取濾波器數據時必須十分小心。sinc濾波器在PWM_SYNC之前的τd啟動,但數據需要2 × τd的時間才能通過濾波器。換言之,必須在PWM_SYNC之后等待τd時間才能從濾波器讀取數據。只有在此刻,電流的真實平均值才可用。與基于SAR的電流測量相比,這種方法在控制時序方面不相同,如圖6所示。
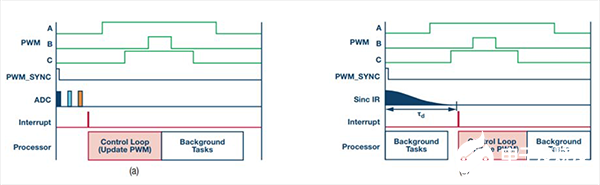
圖6. 控制算法時序,(a)使用SAR ADC,(b)使用Σ-Δ ADC
在SAR情形(a)中,PWM_SYNC脈沖觸發ADC執行若干采樣和轉換。當數據對控制環路而言已就緒時,系統產生一個中斷,控制環路便可開始執行。而在Σ-Δ情形中,不是等待ADC,而是要讓數據完全通過sinc濾波器。當數據就緒時,系統產生一個中斷,指示控制環路可以執行。如果進行類比的話,SAR ADC的轉換時間相當于脈沖響應時間的一半。脈沖響應一半的具體長度取決于調制時鐘和抽取率。對于fM = 20 MHz且DR = 100的典型配置,脈沖響應的一半為τd = 7.4 μs。 雖然比快速SAR ADC略長,但數值差別不大。
應當注意,在典型控制系統中,PWM定時器的零階保持效應遠遠超過脈沖響應的一半,因此sinc濾波器不會嚴重影響環路時序。
Σ-Δ ADC對控制性能的影響
采用Σ-Δ ADC,用戶可以自由選擇sinc濾波器延遲或輸出數據保真度。抽取率較高時,延遲較長,但信號質量較高;抽取率較低時則相反。這種靈活性對于電機控制算法設計十分有利。通常,算法的某些部分對延遲敏感,而對反饋精度較不敏感。其它部分適合在較低動態特性和較高精度下工作,但對延遲較不敏感。舉個例子,考慮圖7(a)所示的常規比例積分控制器(PI)。P部分和I部分采用相同的反饋信號工作,意味著該信號的動態特性必須適合兩種控制路徑。不過,P路徑和I路徑可以分離,如圖7(b)所示。由此還可以再前進一小步,圖7 (c)顯示P路徑和I路徑分離,并且采用具有不同動態特性的反饋信號工作。
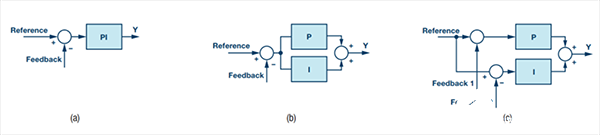
圖7. PI控制器方案。(a)常規方案,(b) P路徑和I路徑分離,(c) P路徑和I路徑分離且反饋分離
P部分的任務是抑制快速負載變化和快速速度變化,但精度不是主要考慮。換言之,低抽取率和短延遲的sinc濾波器對P部分有利。I部分的任務是確保穩態性能穩定且精確,它要求高精度。因此,高抽取率和較長延遲的sinc濾波器對I部分有利。這就產生了圖8所示的實現方案。
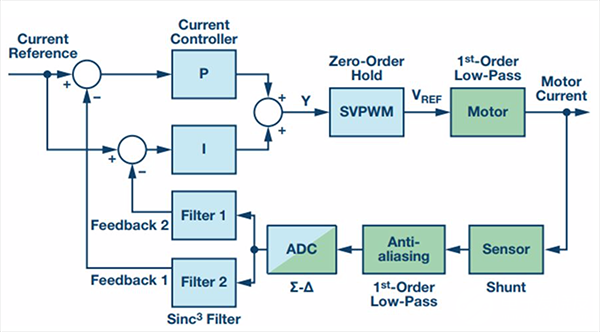
圖8. 雙sinc濾波器和分離的電流控制器P路徑和I路徑
電機相電流由一個傳感器(分流電阻)測量,并流經一個抗混疊濾波器,供應給Σ-Δ ADC。然后,1位數據流輸入兩個sinc濾波器,一個針對P控制器調諧,另一個針對I控制器調諧。為簡明起見,圖8省去了Clark和Park變換。然而,電流控制是在一個旋轉dq框架中完成。
為了評估電流反饋分為兩條路徑的影響,我們對該閉環執行了穩定性分析。對于傳統的Z域分析,sinc濾波器會帶來問題。它會引入一個延遲,對于任何實際抽取率,該延遲小于一個采樣周期。例如,若系統以fsw = 10 kHz的速率運行,濾波器延遲將短于100 μs。從控制環路方面看,sinc模塊是一個小數延遲濾波器。為了模擬小數延遲,將sinc濾波器近似看作一個全通濾波器。在最高為奈奎斯特頻率一半的較低頻率時,該近似處理是精確的,但在更高的頻率,其與理想濾波器有一些偏差。然而,這里的目的是了解雙反饋如何影響環路穩定性,就此而言,該近似是合適的。
作為對比,圖9(a)顯示了反饋路徑(無雙反饋)中僅使用一個sinc濾波器時的閉環幅度響應。開關頻率fsw為10kHz,奈奎斯特頻率設置為5 kHz。在這些系統參數下,對于0 μs至80 μs的sinc濾波器群延遲,繪制閉環響應曲線。注意,群延遲與抽取率直接相關。同預期一樣,低抽取率和群延遲對閉環穩定性的影響很小,但隨著延遲增加,系統阻尼變得越來越小。
圖9. 雙反饋對電流控制性能的影響,(a) sinc濾波器為P控制器和I控制器共用,(b) P控制器和I控制器分別使用單獨的sinc濾波器
現在將反饋分離,使P控制器和I控制器具有單獨的路徑,便可獲得圖9 (b)。這種情況下,用于P控制器的sinc濾波器抽取率是固定值,使得群延遲為10 μs。僅I控制器的抽取率發生變化。
從圖9 (b)可看出,提高I控制器的延遲對閉環穩定性的影響非常小。如上所述,可利用這些特性來提高環路的動態和穩態性能。
本文中,使用分離反饋的算法為PI控制器。不過,這只是一個例子,大多數控制系統都有多個算法,根據動態和精度要求調諧反饋對這些算法是有利的。磁通觀測器、前饋控制器和PID控制器的差分部分就是一些例子。
濾波技術
濾波器的衰減是有限的,逆變器IGBT開關產生的開關噪聲會通過濾波器。本部分探討幫助從電流反饋中消除開關噪聲的技術。
如果電機由電壓源逆變器利用標準空間矢量調制(SVPWM6)驅動,則相電流噪聲頻譜的特征將是邊帶以開關頻率整數倍為中心分布。例如,若使用10 kHz開關頻率,則在n × 10 kHz周圍會有高噪聲電平(n為整數)。典型頻譜如圖10中的綠色曲線所示。這些邊帶會在電流反饋中引入噪聲,因此需要予以有效衰減。
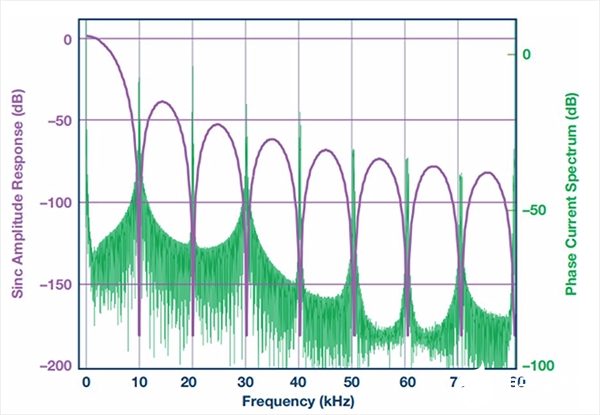
圖10. 相電流功率頻譜(綠色)和sinc濾波器幅度響應(紫色)
sinc濾波器的極點和零點位置由抽取率和調制頻率決定。這說明,用戶可以自由地調諧濾波器頻率響應以便最好地支持應用。三階sinc濾波器的幅度響應如圖10中紫色曲線所示。同預期一樣,幅度在較高頻率時縮小,但幅度也有特征陷波頻率;在這些頻率,衰減趨近無限大。陷波頻率由調制器時鐘和抽取率決定:
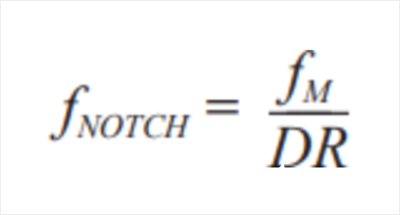
如果陷波頻率與相電流頻譜的邊帶相同,就能非常有效地衰減逆變器開關噪聲。舉個例子,考慮逆變器開關頻率fsw為 10 kHz,ADC調制器時鐘fM為8 MHz,抽取率DR為800。這樣,陷波頻率為n × 10 kHz,響應如圖10所示。注意每個邊帶是如何被陷波衰減的。
sinc濾波器的某些硬件實現方案不支持高抽取率,因而無法將極點/零點置于PWM頻率。另外,與高抽取率相關的濾波器群延遲可能也是無法接受的。在圖10所示例子中,800的抽取率和 8 MHz的調制頻率產生的延遲為150 μs。
另一種方法是讓sinc濾波器以較低抽取率運行,然后在軟件中對數據進行后期處理。仍然假設fsw = 10 kHz且fM = 8 MHz,一種可能的方法是讓硬件sinc濾波器以200的抽取率運行,因此,數據速率為8 MHz/200 = 40 kHz。這一數據速率對電機控制算法而言太高,可以引入一個軟件濾波器,將數據速率降至10 kHz。這種濾波器的一個例子就是抽取率為4(相當于4個樣本的移動平均值)的一階sinc濾波器。其配置如圖11所示。
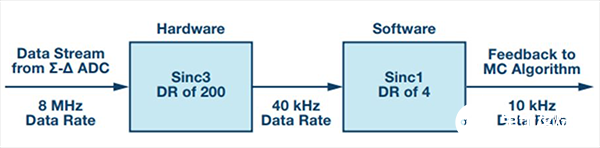
圖11. 硬件和軟件sinc濾波器組合
硬件濾波器以高于控制算法需要的速率輸出數據,因此,軟件濾波器給信號增加的延遲非常小,遠小于直接使用硬件濾波器進行抽取以降低至控制算法更新速率這種情況下的延遲。此外,sinc1濾波器仍會在相電流頻譜的所有邊帶處設置一個陷波頻率。故而,對逆變器產生的開關噪聲進行有效衰減的優勢仍然存在。
濾波技術可以與分離反饋路徑方法一起使用。由于硬件和軟件sinc濾波器組合提供非常高的衰減,但會給電流反饋帶來一定的延遲,因此濾波技術最適合于I路徑。
實現和測試
本文所述的概念已在ADI公司的一個400 V電機控制平臺上得到實現和驗證,如圖12所示。電源板提供110 VAC/230 VAC通用輸入電壓、boost功率系數校正以及5 AMPS額定連續電流的三相IGBT逆變器。電機為帶遞增編碼器反饋的Kollmorgen AKM22三相PM伺服電機。用于電流反饋的Σ-Δ ADC為AD7403。Σ-Δ ADC與處理器ADSP-CM408直接接口,后者內置sinc濾波器,支持本文所述的技術。
圖12. 用于評估的硬件平臺
結論
盡管缺少明確定義的采樣時刻,但Σ-Δ轉換可用來測量電機電流而不會有混疊效應。本文所述技術可將sinc濾波器對PWM信號的脈沖響應正確對齊。以PI控制器為例,本文說明可以調諧兩個并聯sinc濾波器來滿足控制算法的要求,從而改善帶寬和穩態性能。
最后,本文討論了如何精心定位sinc濾波器零點以幫助消除電流反饋中的開關噪聲。所有這些概念都在一臺驅動永磁電機的400 V逆變器上得到了實現和驗證。
審核編輯:何安
-
adc
+關注
關注
98文章
6524瀏覽量
545201 -
電機驅動
+關注
關注
60文章
1219瀏覽量
86835
發布評論請先 登錄
相關推薦
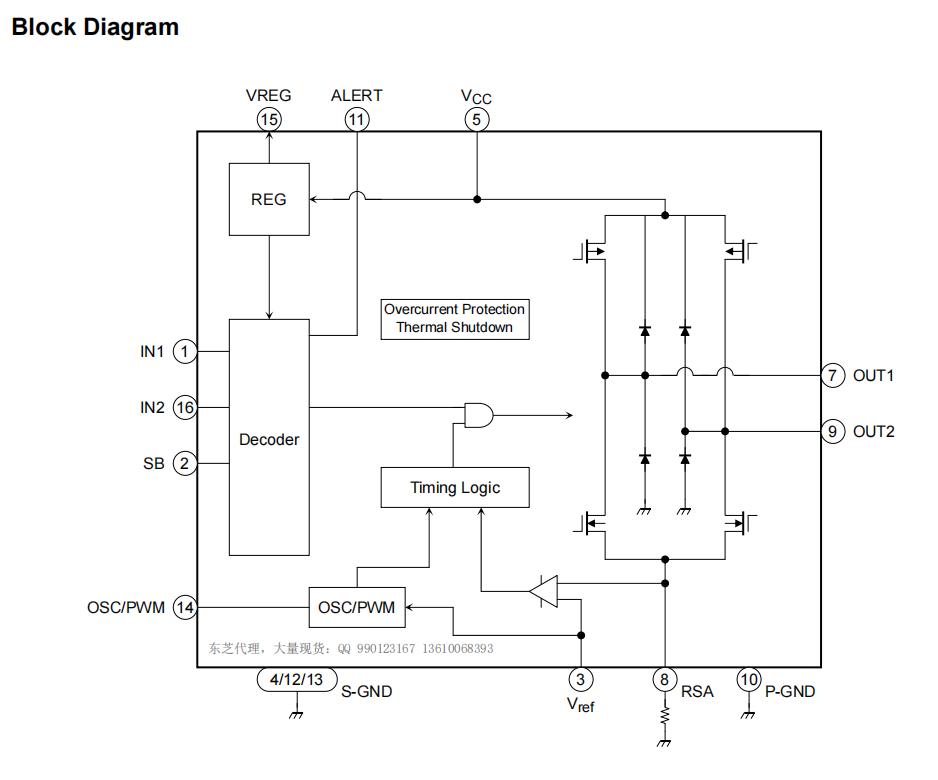
高性能步進電機驅動器:TB6559FG的優勢與應用
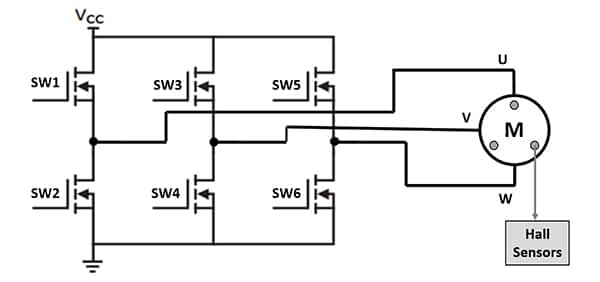
為什么BLDC電機驅動方案是高速鼓風機的最佳選擇?

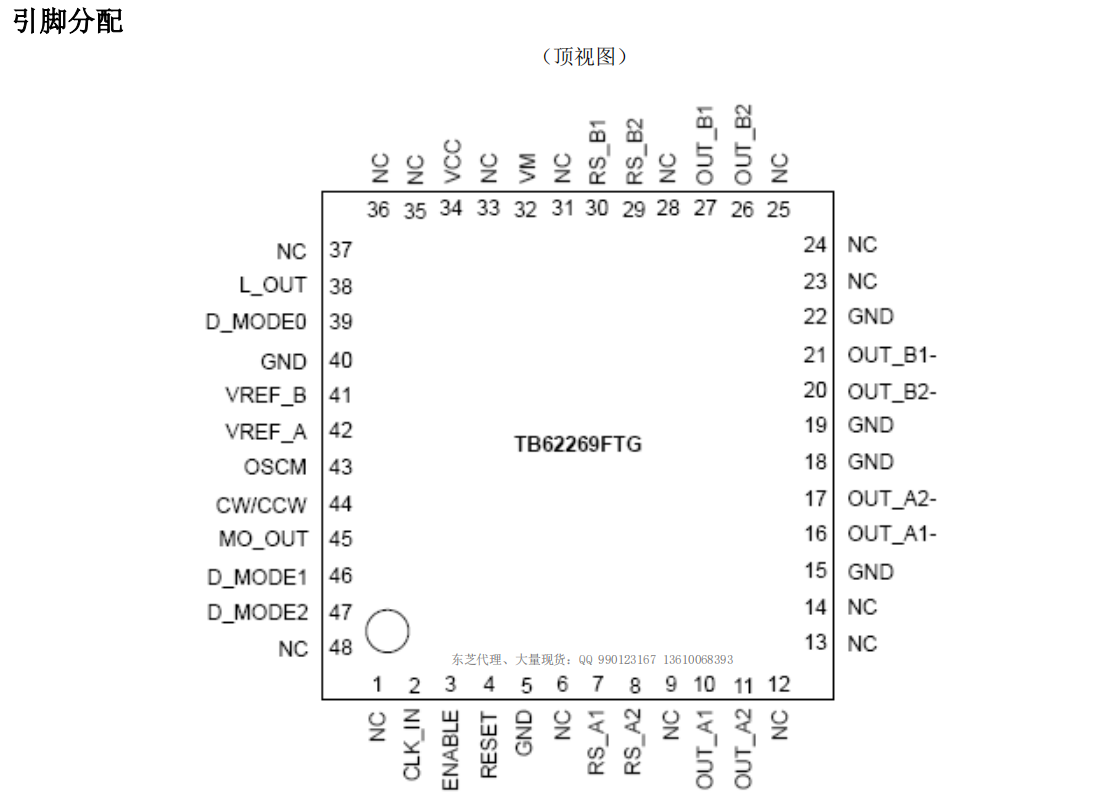
高性能步進電機驅動芯片 TB62269FTG
電機矢量控制技術在工業應用中的實現
新應用:無刷云臺電機驅動應用中的電機驅動芯片

ATA-4051高壓功率放大器在非共振式壓電直線電機性能測試中的應用
如何在挑戰性環境中優化 BLDC 電機驅動器的熱性能




 如何在電機驅動中實現最佳性能
如何在電機驅動中實現最佳性能














評論