近期我會一連幾篇談談bert中的關鍵細節,這個position encoding是我看到的bert(實質上是transformer中提出的)中最為驚喜的但是卻被很多人忽略(可以理解為媒體鼓吹最少的)一個細節,這里給大家談談。
什么是position encoding
顧名思義,就是基于位置的一套詞嵌入方法,說得簡單點,就是對于一個句子,都有對應的一個向量。
position encoding的收益
我感覺要做一個事情,首先還是要看他的出發點和收益,說白了就是優點是啥,做這個的目標是啥,這樣我們才知道怎么做。
回頭看看CNN結構、RNN甚至是transformer的self-attention,其實都沒有特別關注位置信息,而實際上,我們卻是需要去關注的,畢竟作為一門語言,他大都有比較嚴謹的語法結構,特定詞匯還真的會出現在特定位置,這是非常有意思的,來看看例子(來源于知乎):
I like this movie because it doesn't have an overhead history.I don't like this movie because it has an overhead history.
從情感上,上面是正面,下面是負面,這個非常顯而易見,因為這個否定句,從實體提取的角度都有movie和history,無論是哪個任務,都可以看到一個語法結構中存在的位置信息。
對CNN,只能考慮到固定前后的局部信息,RNN能考慮稍微長期的信息,LSTM是有重點的記錄,Transformer只能考慮到全局的信息,尤其在bert中,只用了transformer encoder,模型上就完全喪失對位置信息的描述了,因此引入基于位置的特征就可能在特定任務中產生收益。
換個角度再看一個例子:
I believe I can be the best.
對于self attention,如果沒有positional encoding,兩個i的輸出將會一樣,但是我們知道,這兩個i是存在區別的,不是在指代上,而是含義上,第一個i是觀點的發出者,“不要你覺得,我要我覺得”,第二個i是觀點的對象,“認為我會是最棒的,不是別人”,所以從語義上兩者就有所區別了,權重向量完全一樣可就有問題了吧。這也是缺少位置信息的缺憾。
position embedding怎么做
首先,最簡單的模式就是對詞向量矩陣直接加一層全連接層,就是全連接層。就真的是這么簡單!
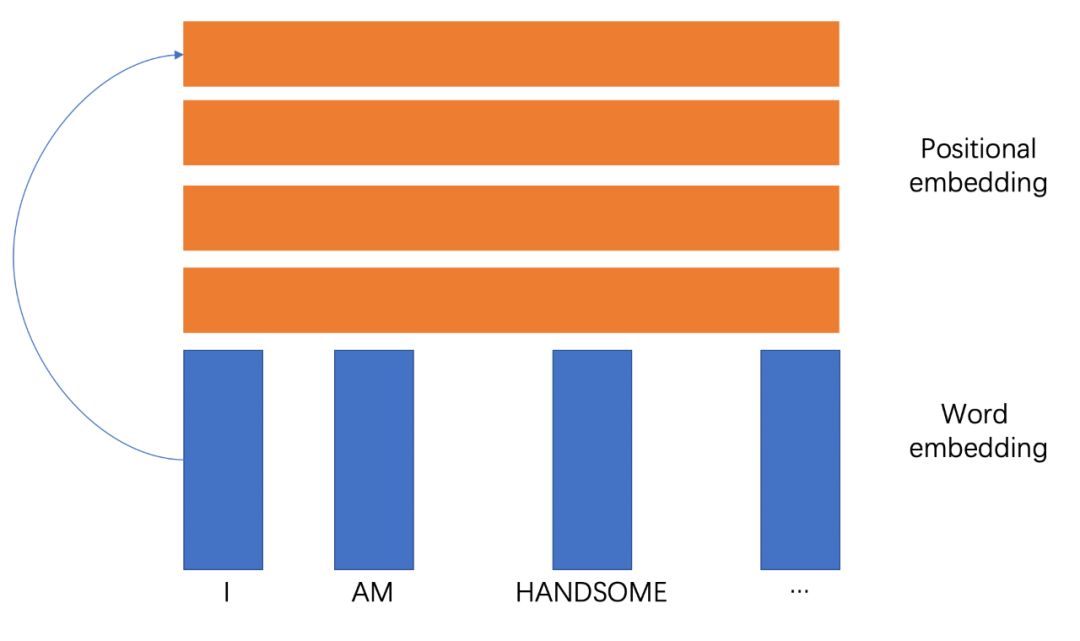
對于每個位置的詞向量,都穩定的乘以一個穩定的向量,就如上面所示,第1個位置一定對應positonal embedding的第一個向量,那這組向量抽出來,不是positional embedding是啥。
但當然的,這里就有很大的問題,那就是這只是絕對位置,看上面第一個例子(我再搬運一遍):
I like this movie because it doesn't have an overhead history.I don't like this movie because it has an overhead history.
這里的like 和 don't like可就不是一個位置了吧,所以絕對位置肯定是有問題的,那么就要引入相對位置的概念了。來看看transformer論文里面是怎么說的(我把解釋也給大家搬過來了):

這里用的是兩種三角函數,可以說是非常巧妙了,我們來慢慢分析。上代碼!
import matplotlib.pyplot as plt
import math
def positional_enc(i,pos):
return math.sin(pos /10000**(i/100))
x = []
for idx in range(10):
tmp_x = list(range(1,100))
tmp_y = [positional_enc(i, idx) for i in tmp_x]
plt.plot(tmp_x,tmp_y,label=str(idx))
plt.legend(loc = 'upper right')
plt.show()
代碼跑出來是這樣的:
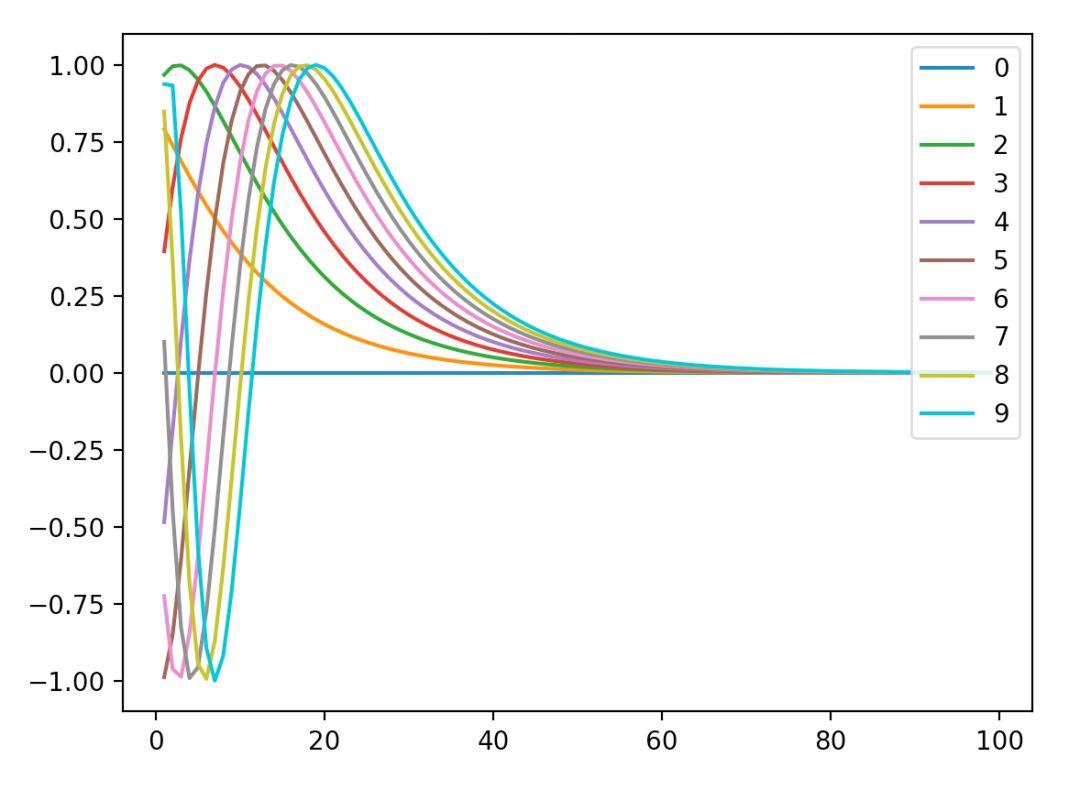
橫坐標是維數上的每個值,縱坐標是對應的sin值,圖例對應句子中的每個位置。
首先看維數位置-sin值之間的關系,很明顯,我們沒有發現周期性,最終往0處收斂,我們也可以知道了,在這種emcoding下,其實維數沒必要太高了。
而對于位置-sini值之間的關系,可以整個曲線是會朝著右邊移動的,從權重角度看,實質上就是每一個維度都會有一個比較看重的句子位置,其他位置說白了就是不看了,而前面的甚至可能為負,主要原因是要拋棄以前的信息,這樣多個維度就能把多個位置都當做了重點來看。
周期性去了哪里呢,其實在這里,再來上代碼:
import matplotlib.pyplot as plt
import math
def positional_emb(i,pos):
return math.sin(pos /10000**(i/100))
tmp_x = list(range(20))
tmp_y = [positional_emb(10, i) for i in tmp_x]
plt.plot(tmp_x,tmp_y)
plt.show()
得到了有周期性的圖。
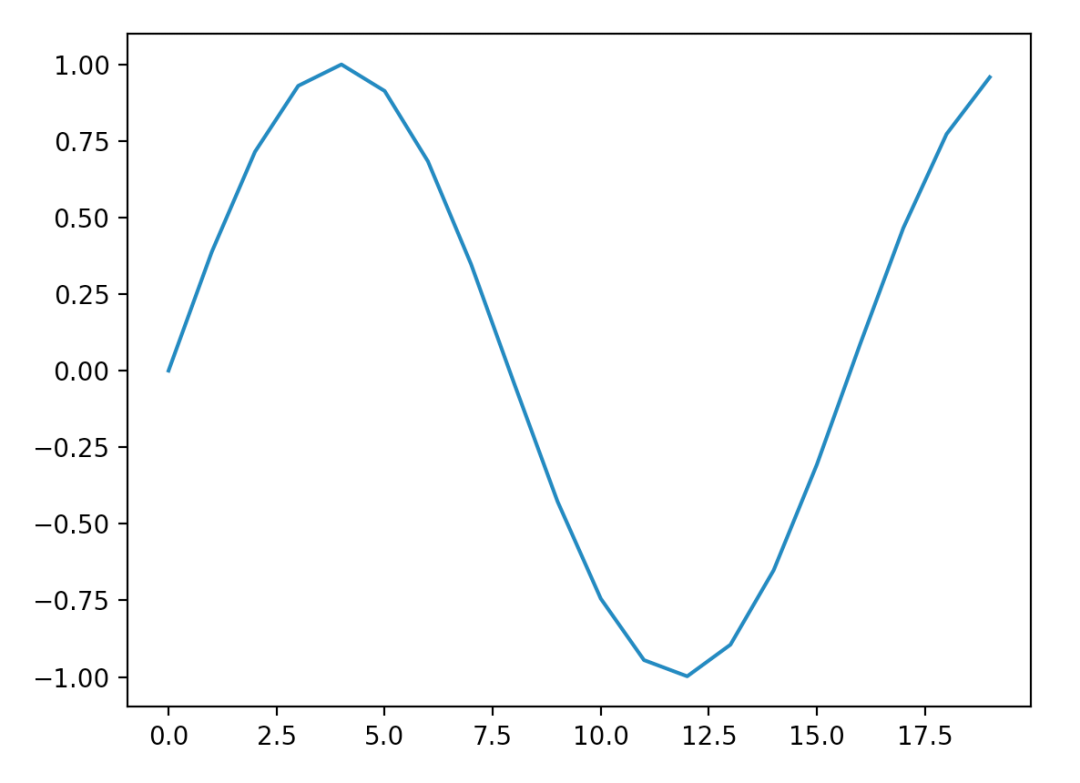
周期性只體現在位置和整個函數結果的關系,而具體的波長,其實是由positional encoding向量決定的。
不得不說,這個函數的設計可謂是對現實場景有了十分充分的理解,抽象非常精準。
預測效果
首先來看看兩種positional encoding的具體效果,來自transformer的對比。
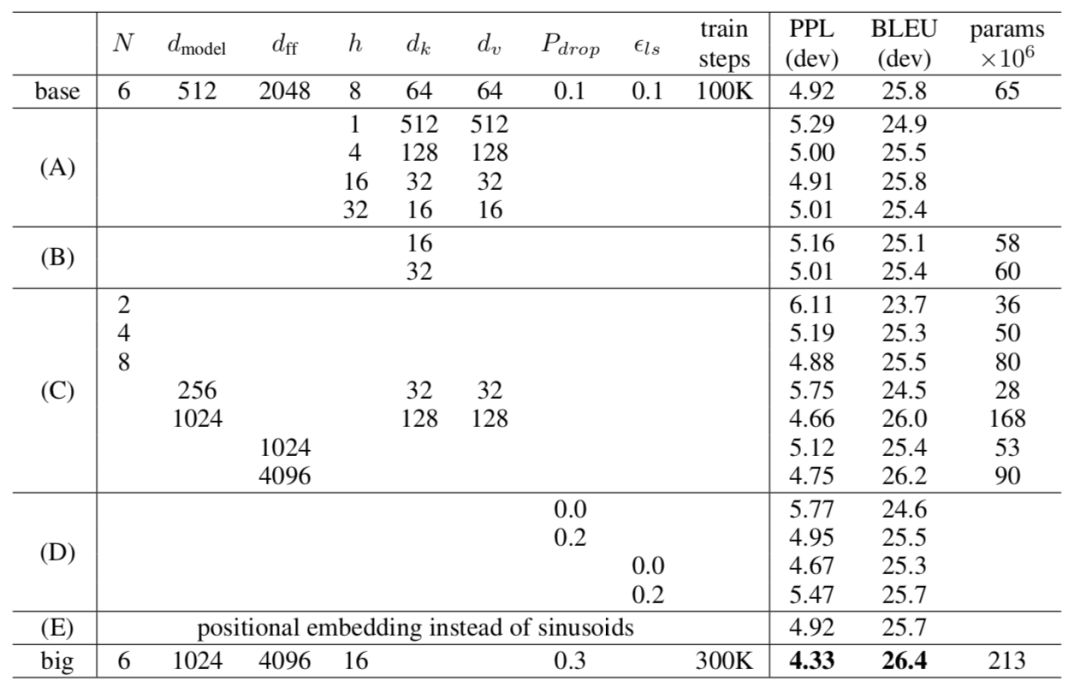
主要看E、base和big。其實可以看到posiitional emb本身的效果其實還行,與base相當,說明還是有不小收益的。
來看看源碼
原理是看完了,來看看源碼吧。
def positional_encoding(inputs,
maxlen,
masking=True,
scope="positional_encoding"):
'''Sinusoidal Positional_Encoding. See 3.5
inputs: 3d tensor. (N, T, E)
maxlen: scalar. Must be >= T
masking: Boolean. If True, padding positions are set to zeros.
scope: Optional scope for `variable_scope`.
returns
3d tensor that has the same shape as inputs.
'''
E = inputs.get_shape().as_list()[-1] # static
N, T = tf.shape(inputs)[0], tf.shape(inputs)[1] # dynamic
with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# position indices
position_ind = tf.tile(tf.expand_dims(tf.range(T), 0), [N, 1]) # (N, T)
# First part of the PE function: sin and cos argument
position_enc = np.array([
[pos / np.power(10000, (i-i%2)/E) for i in range(E)]
for pos in range(maxlen)])
# Second part, apply the cosine to even columns and sin to odds.
position_enc[:, 0::2] = np.sin(position_enc[:, 0::2]) # dim 2i
position_enc[:, 1::2] = np.cos(position_enc[:, 1::2]) # dim 2i+1
position_enc = tf.convert_to_tensor(position_enc, tf.float32) # (maxlen, E)
# lookup
outputs = tf.nn.embedding_lookup(position_enc, position_ind)
# masks
if masking:
outputs = tf.where(tf.equal(inputs, 0), inputs, outputs)
return tf.to_float(outputs)
本身公式上沒有想象的復雜,但是這里面其實展現了很多python相關的技巧。
這里的計算并非全都使用的tf,對positionenc,前面用numpy進行計算,然后用embeddinglookup的方式引入。
position_enc[:,0::2]和position_enc[:,1::2]來自numpy語法,避免了寫循環和條件語句就能夠完成奇數偶數計算。
另外是有很多可能在各種教材或者教程中沒有的函數工具,大家可以多看看學學。
tf.AUTO_REUSE:批量化共享變量作用域的方法。
tf.tile():張量擴展,對當前張量內的數據進行一定規則的復制,保證輸出張量維度不變。
責任編輯:xj
原文標題:bert之我見 - positional encoding
文章出處:【微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
-
深度學習
+關注
關注
73文章
5507瀏覽量
121299 -
自然語言
+關注
關注
1文章
288瀏覽量
13365 -
nlp
+關注
關注
1文章
489瀏覽量
22059
原文標題:bert之我見 - positional encoding
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 positional encoding詳解
positional encoding詳解















評論