今天早上在reddit上刷到一張非常形象mó xìng的圖,
那就讓我們來整理一下深度學(xué)習(xí)中離不開的激活函數(shù)!
激活函數(shù)(Activation Function)是一種添加到人工神經(jīng)網(wǎng)絡(luò)中的函數(shù),旨在幫助網(wǎng)絡(luò)學(xué)習(xí)數(shù)據(jù)中的復(fù)雜模式。類似于人類大腦中基于神經(jīng)元的模型,激活函數(shù)最終決定了要發(fā)射給下一個(gè)神經(jīng)元的內(nèi)容。
在人工神經(jīng)網(wǎng)絡(luò)中,一個(gè)節(jié)點(diǎn)的激活函數(shù)定義了該節(jié)點(diǎn)在給定的輸入或輸入集合下的輸出。標(biāo)準(zhǔn)的計(jì)算機(jī)芯片電路可以看作是根據(jù)輸入得到開(1)或關(guān)(0)輸出的數(shù)字電路激活函數(shù)。因此,激活函數(shù)是確定神經(jīng)網(wǎng)絡(luò)輸出的數(shù)學(xué)方程式,本文概述了深度學(xué)習(xí)中常見的十種激活函數(shù)及其優(yōu)缺點(diǎn)。
首先我們來了解一下人工神經(jīng)元的工作原理,大致如下:
上述過程的數(shù)學(xué)可視化過程如下圖所示:
1. Sigmoid 激活函數(shù)
Sigmoid 函數(shù)的圖像看起來像一個(gè) S 形曲線。
函數(shù)表達(dá)式如下:
在什么情況下適合使用 Sigmoid 激活函數(shù)呢?
Sigmoid 函數(shù)的輸出范圍是 0 到 1。由于輸出值限定在 0 到 1,因此它對(duì)每個(gè)神經(jīng)元的輸出進(jìn)行了歸一化;
用于將預(yù)測(cè)概率作為輸出的模型。由于概率的取值范圍是 0 到 1,因此 Sigmoid 函數(shù)非常合適;
梯度平滑,避免「跳躍」的輸出值;
函數(shù)是可微的。這意味著可以找到任意兩個(gè)點(diǎn)的 sigmoid 曲線的斜率;
明確的預(yù)測(cè),即非常接近 1 或 0。
Sigmoid 激活函數(shù)有哪些缺點(diǎn)?
傾向于梯度消失;
函數(shù)輸出不是以 0 為中心的,這會(huì)降低權(quán)重更新的效率;
Sigmoid 函數(shù)執(zhí)行指數(shù)運(yùn)算,計(jì)算機(jī)運(yùn)行得較慢。
2. Tanh / 雙曲正切激活函數(shù)
tanh 激活函數(shù)的圖像也是 S 形,表達(dá)式如下:
tanh 是一個(gè)雙曲正切函數(shù)。tanh 函數(shù)和 sigmoid 函數(shù)的曲線相對(duì)相似。但是它比 sigmoid 函數(shù)更有一些優(yōu)勢(shì)。
首先,當(dāng)輸入較大或較小時(shí),輸出幾乎是平滑的并且梯度較小,這不利于權(quán)重更新。二者的區(qū)別在于輸出間隔,tanh 的輸出間隔為 1,并且整個(gè)函數(shù)以 0 為中心,比 sigmoid 函數(shù)更好;
在 tanh 圖中,負(fù)輸入將被強(qiáng)映射為負(fù),而零輸入被映射為接近零。
注意:在一般的二元分類問題中,tanh 函數(shù)用于隱藏層,而 sigmoid 函數(shù)用于輸出層,但這并不是固定的,需要根據(jù)特定問題進(jìn)行調(diào)整。
3. ReLU 激活函數(shù)
ReLU 激活函數(shù)圖像如上圖所示,函數(shù)表達(dá)式如下:

ReLU 函數(shù)是深度學(xué)習(xí)中較為流行的一種激活函數(shù),相比于 sigmoid 函數(shù)和 tanh 函數(shù),它具有如下優(yōu)點(diǎn):
當(dāng)輸入為正時(shí),不存在梯度飽和問題。
計(jì)算速度快得多。ReLU 函數(shù)中只存在線性關(guān)系,因此它的計(jì)算速度比 sigmoid 和 tanh 更快。
當(dāng)然,它也有缺點(diǎn):
Dead ReLU 問題。當(dāng)輸入為負(fù)時(shí),ReLU 完全失效,在正向傳播過程中,這不是問題。有些區(qū)域很敏感,有些則不敏感。但是在反向傳播過程中,如果輸入負(fù)數(shù),則梯度將完全為零,sigmoid 函數(shù)和 tanh 函數(shù)也具有相同的問題;
我們發(fā)現(xiàn) ReLU 函數(shù)的輸出為 0 或正數(shù),這意味著 ReLU 函數(shù)不是以 0 為中心的函數(shù)。
4. Leaky ReLU
它是一種專門設(shè)計(jì)用于解決 Dead ReLU 問題的激活函數(shù):
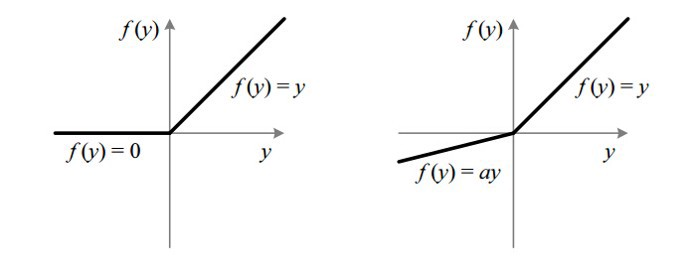
ReLU vs Leaky ReLU
為什么 Leaky ReLU 比 ReLU 更好?
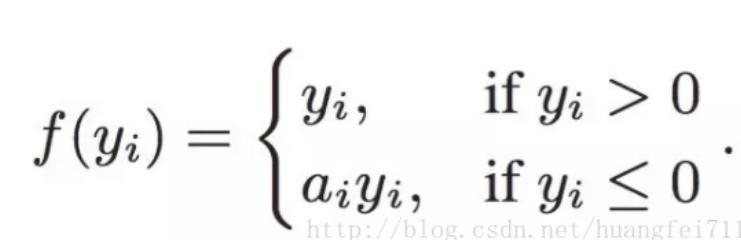
Leaky ReLU 通過把 x 的非常小的線性分量給予負(fù)輸入(0.01x)來調(diào)整負(fù)值的零梯度(zero gradients)問題;
leak 有助于擴(kuò)大 ReLU 函數(shù)的范圍,通常 a 的值為 0.01 左右;
Leaky ReLU 的函數(shù)范圍是(負(fù)無窮到正無窮)。
注意:從理論上講,Leaky ReLU 具有 ReLU 的所有優(yōu)點(diǎn),而且 Dead ReLU 不會(huì)有任何問題,但在實(shí)際操作中,尚未完全證明 Leaky ReLU 總是比 ReLU 更好。
5. ELU
ELU vs Leaky ReLU vs ReLU
ELU 的提出也解決了 ReLU 的問題。與 ReLU 相比,ELU 有負(fù)值,這會(huì)使激活的平均值接近零。均值激活接近于零可以使學(xué)習(xí)更快,因?yàn)樗鼈兪固荻雀咏匀惶荻取?/p>
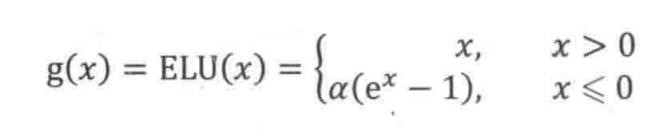
顯然,ELU 具有 ReLU 的所有優(yōu)點(diǎn),并且:
沒有 Dead ReLU 問題,輸出的平均值接近 0,以 0 為中心;
ELU 通過減少偏置偏移的影響,使正常梯度更接近于單位自然梯度,從而使均值向零加速學(xué)習(xí);
ELU 在較小的輸入下會(huì)飽和至負(fù)值,從而減少前向傳播的變異和信息。
一個(gè)小問題是它的計(jì)算強(qiáng)度更高。與 Leaky ReLU 類似,盡管理論上比 ReLU 要好,但目前在實(shí)踐中沒有充分的證據(jù)表明 ELU 總是比 ReLU 好。
6. PReLU(Parametric ReLU)
PReLU 也是 ReLU 的改進(jìn)版本:
看一下 PReLU 的公式:參數(shù)α通常為 0 到 1 之間的數(shù)字,并且通常相對(duì)較小。
如果 a_i= 0,則 f 變?yōu)?ReLU
如果 a_i》 0,則 f 變?yōu)?leaky ReLU
如果 a_i 是可學(xué)習(xí)的參數(shù),則 f 變?yōu)?PReLU
PReLU 的優(yōu)點(diǎn)如下:
在負(fù)值域,PReLU 的斜率較小,這也可以避免 Dead ReLU 問題。
與 ELU 相比,PReLU 在負(fù)值域是線性運(yùn)算。盡管斜率很小,但不會(huì)趨于 0。
7. Softmax
Softmax 是用于多類分類問題的激活函數(shù),在多類分類問題中,超過兩個(gè)類標(biāo)簽則需要類成員關(guān)系。對(duì)于長(zhǎng)度為 K 的任意實(shí)向量,Softmax 可以將其壓縮為長(zhǎng)度為 K,值在(0,1)范圍內(nèi),并且向量中元素的總和為 1 的實(shí)向量。
Softmax 與正常的 max 函數(shù)不同:max 函數(shù)僅輸出最大值,但 Softmax 確保較小的值具有較小的概率,并且不會(huì)直接丟棄。我們可以認(rèn)為它是 argmax 函數(shù)的概率版本或「soft」版本。
Softmax 函數(shù)的分母結(jié)合了原始輸出值的所有因子,這意味著 Softmax 函數(shù)獲得的各種概率彼此相關(guān)。
Softmax 激活函數(shù)的主要缺點(diǎn)是:
在零點(diǎn)不可微;
負(fù)輸入的梯度為零,這意味著對(duì)于該區(qū)域的激活,權(quán)重不會(huì)在反向傳播期間更新,因此會(huì)產(chǎn)生永不激活的死亡神經(jīng)元。
8. Swish
函數(shù)表達(dá)式:y = x * sigmoid (x)
Swish 的設(shè)計(jì)受到了 LSTM 和高速網(wǎng)絡(luò)中 gating 的 sigmoid 函數(shù)使用的啟發(fā)。我們使用相同的 gating 值來簡(jiǎn)化 gating 機(jī)制,這稱為 self-gating。
self-gating 的優(yōu)點(diǎn)在于它只需要簡(jiǎn)單的標(biāo)量輸入,而普通的 gating 則需要多個(gè)標(biāo)量輸入。這使得諸如 Swish 之類的 self-gated 激活函數(shù)能夠輕松替換以單個(gè)標(biāo)量為輸入的激活函數(shù)(例如 ReLU),而無需更改隱藏容量或參數(shù)數(shù)量。
Swish 激活函數(shù)的主要優(yōu)點(diǎn)如下:
「無界性」有助于防止慢速訓(xùn)練期間,梯度逐漸接近 0 并導(dǎo)致飽和;(同時(shí),有界性也是有優(yōu)勢(shì)的,因?yàn)橛薪缂せ詈瘮?shù)可以具有很強(qiáng)的正則化,并且較大的負(fù)輸入問題也能解決);
導(dǎo)數(shù)恒 》 0;
平滑度在優(yōu)化和泛化中起了重要作用。
9. Maxout
在 Maxout 層,激活函數(shù)是輸入的最大值,因此只有 2 個(gè) maxout 節(jié)點(diǎn)的多層感知機(jī)就可以擬合任意的凸函數(shù)。
單個(gè) Maxout 節(jié)點(diǎn)可以解釋為對(duì)一個(gè)實(shí)值函數(shù)進(jìn)行分段線性近似 (PWL) ,其中函數(shù)圖上任意兩點(diǎn)之間的線段位于圖(凸函數(shù))的上方。
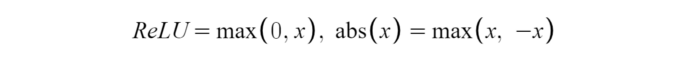
Maxout 也可以對(duì) d 維向量(V)實(shí)現(xiàn):
假設(shè)兩個(gè)凸函數(shù) h_1(x) 和 h_2(x),由兩個(gè) Maxout 節(jié)點(diǎn)近似化,函數(shù) g(x) 是連續(xù)的 PWL 函數(shù)。
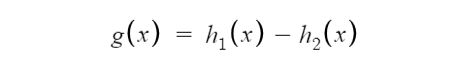
因此,由兩個(gè) Maxout 節(jié)點(diǎn)組成的 Maxout 層可以很好地近似任何連續(xù)函數(shù)。
10. Softplus
Softplus 函數(shù):f(x)= ln(1 + exp x)
Softplus 的導(dǎo)數(shù)為
f ′(x)=exp(x) / ( 1+exp? x )
= 1/ (1 +exp(?x ))
,也稱為 logistic / sigmoid 函數(shù)。
Softplus 函數(shù)類似于 ReLU 函數(shù),但是相對(duì)較平滑,像 ReLU 一樣是單側(cè)抑制。它的接受范圍很廣:(0, + inf)。
編輯:lyn
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4333瀏覽量
62705 -
深度學(xué)習(xí)
+關(guān)注
關(guān)注
73文章
5504瀏覽量
121239
原文標(biāo)題:深度學(xué)習(xí)最常用的10個(gè)激活函數(shù)!
文章出處:【微信號(hào):zenRRan,微信公眾號(hào):深度學(xué)習(xí)自然語言處理】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
labview常用的基本函數(shù)
利用Matlab函數(shù)實(shí)現(xiàn)深度學(xué)習(xí)算法
神經(jīng)元模型激活函數(shù)通常有哪幾類
深度學(xué)習(xí)中的時(shí)間序列分類方法
前饋神經(jīng)網(wǎng)絡(luò)的基本結(jié)構(gòu)和常見激活函數(shù)
深度學(xué)習(xí)常用的Python庫
BP神經(jīng)網(wǎng)絡(luò)激活函數(shù)怎么選擇
卷積神經(jīng)網(wǎng)絡(luò)激活函數(shù)的作用
神經(jīng)網(wǎng)絡(luò)中激活函數(shù)的定義及類型
深度學(xué)習(xí)模型訓(xùn)練過程詳解
神經(jīng)網(wǎng)絡(luò)中的激活函數(shù)有哪些
MATLAB信號(hào)處理常用函數(shù)詳解
PyTorch中激活函數(shù)的全面概覽
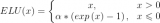
詳解深度學(xué)習(xí)、神經(jīng)網(wǎng)絡(luò)與卷積神經(jīng)網(wǎng)絡(luò)的應(yīng)用





 關(guān)于深度學(xué)習(xí)最常用的10大激活函數(shù)詳解
關(guān)于深度學(xué)習(xí)最常用的10大激活函數(shù)詳解











評(píng)論