拓撲學（名詞解釋）是數學的一個分支，主要關注幾何圖形在連續形變后還能保持不變的一些性質。簡單來講，物體的拓撲數可以由其開孔數量決定，例如一個球形的實心橡皮泥和勺子的開孔數為零，可以視為同一類拓撲相，而甜甜圈的開孔數為一，則為另外一類拓撲相。

近幾十年來，物理學家將拓撲學的概念引入凝聚態物理，三位先驅者David J. Thouless、F. Duncan M. Haldane 和J. Michael Kosterlitz 也因為他們在拓撲相變和拓撲物態方面的貢獻獲得2016年諾貝爾物理學獎。

除凝聚態物理之外，科學家還將拓撲學的概念引入到光學，逐步發展出了拓撲光子學領域。通過將光子晶體能帶理論和拓撲學結合，人們實現了多種光學拓撲態，具有許多新奇特性（例如完全抑制背散射等），在光通訊、光學集成和光子計算機等領域有巨大的應用潛力。

迄今為止，光學拓撲態的實驗研究大多是在光波長較長的頻段（例如微波），這是因為實現拓撲態往往需要破壞體系對稱性，涉及復雜的結構設計。當光波長變小時（例如紅外或可見頻段），需要在納米及以下尺度進行精細的結構設計，目前還受限于微納加工的技術手段。因此，在納米光子學領域（致力于在納米尺度上實現光子操控）拓撲學還是一個比較陌生的概念。

2018年，W.Ma 等人（代表論文：Nature 2018， 562， 557 | 原文閱讀）發現在一種天然的范德瓦爾斯晶體（α相氧化鉬：α-MoO3）中存在聲子極化激元（名詞解釋）。與之前觀測到的極化激元不同的是，α-MoO3聲子極化激元只能沿著特定的晶體方向（名詞解釋）傳播，這是因為氧化鉬是一種面內各向異性材料，即沿［100］和［001］晶體方向的介電常數不相等且為異號。

通過實驗發現，α-MoO3聲子極化激元的面內等頻線（iso-frequency curve）是雙曲線，這與常見的各向同性材料中閉合的圓形等頻線非常不同。

基于上述發現，近期西班牙奧維耶多大學量子納米光學小組報道了兩種類型的光學拓撲轉變（圖1）。通過旋轉雙層氧化鉬晶體或調控其介電環境，實現了光學拓撲轉變的直接觀測。這項研究有助于在納米尺度下實現紅外光的人為調控和高度定向傳播。

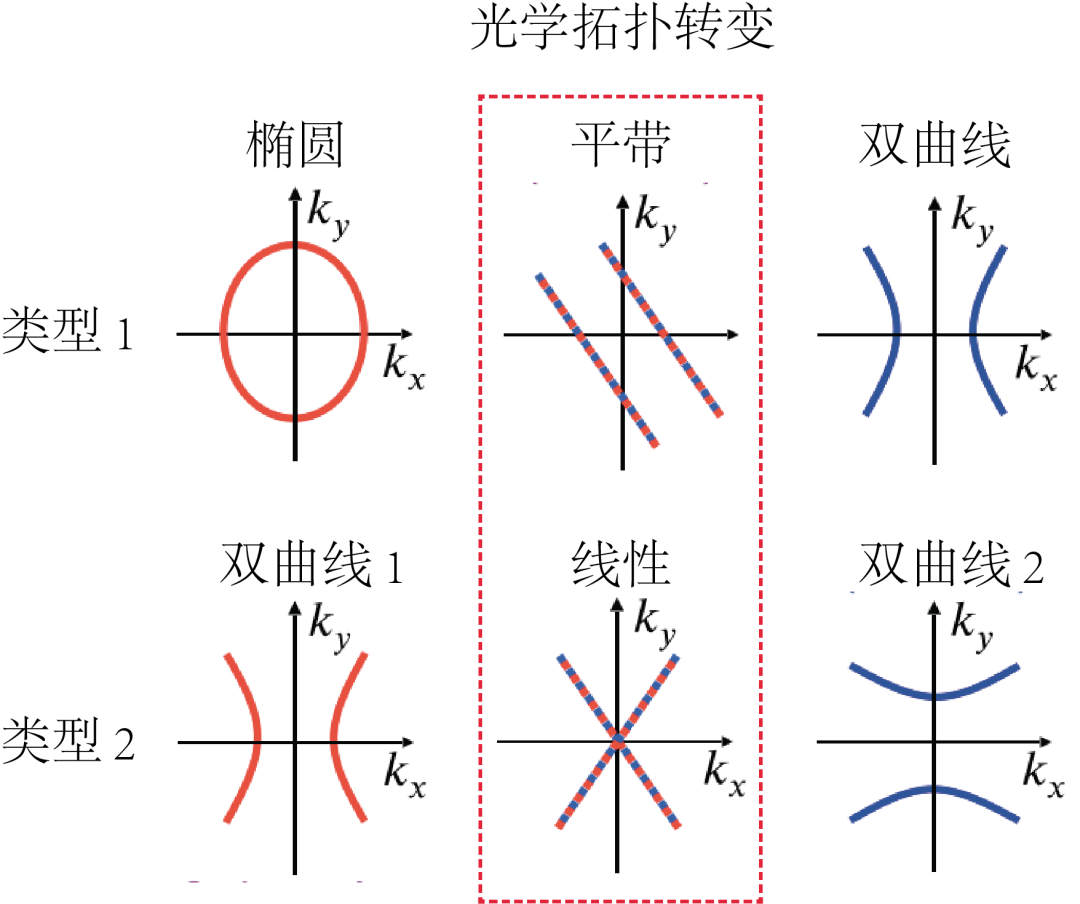
圖1 兩種類型的光學拓撲轉變。

圖中所示為極化激元的面內等頻線。

在第一類拓撲轉變中，

等頻線由閉合的橢圓型變為開放的雙曲線型。

第二類拓撲轉變中，

雙曲線型等頻線閉合于一點然后重新打開并旋轉了90度。

該成果分別以 Twisted Nano-Optics： Manipulating Light at the Nanoscale with Twisted Phonon Polaritonic Slabs 和 Enabling propagation of anisotropic polaritons along forbidden directions via a topological transition 為題發表在 Nano Letters 和 Science Advances。

第一類光學拓撲轉變

理論研究表明當把兩層氧化鉬晶體疊加并且旋轉一個固定角度時，由于層與層之間的電磁場耦合作用，聲子極化激元的等頻線會產生明顯的變化，從而影響其傳播（如圖2所示）。

當轉角為零度時，疊層氧化鉬和單層氧化鉬表現出類似的性質，極化激元的內陷型波前沿著［100］方向傳播，即等頻線為中心軸沿著［100］方向的雙曲線；

當轉角增大到63度時，極化激元變為沿固定角度高度定向傳播，這說明其等頻線變為了平帶；

當轉角繼續增大到90度，極化激元可以沿所有面內方向傳播，表明了閉合型等頻線。

等頻線從開口到閉合，說明其經歷了拓撲轉變。

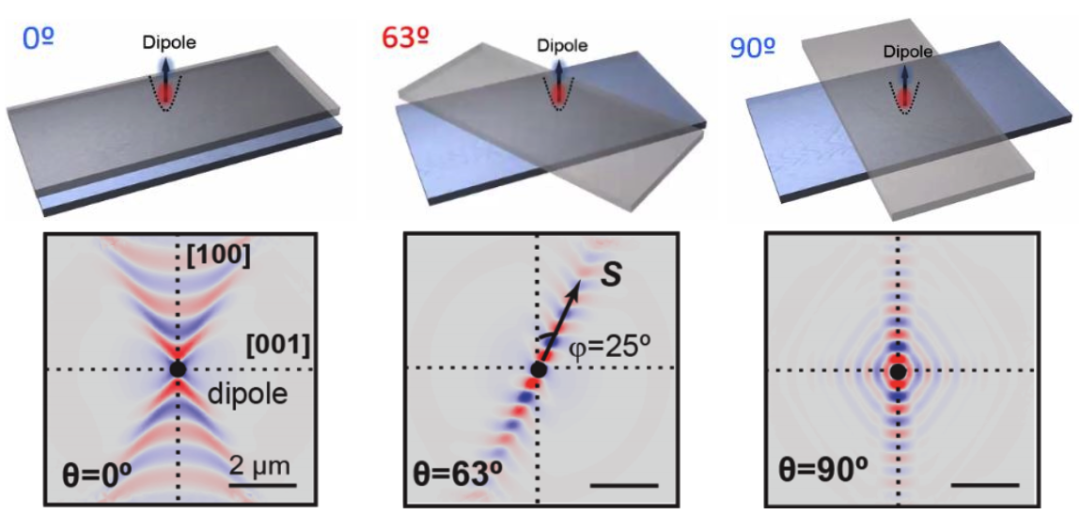
圖2 光學拓撲轉變的理論研究。

當雙層氧化鉬轉角從零增大到90度時，

極化激元的傳播方式發生了明顯變化，

其等頻線經歷了從開口到閉合的拓撲轉變。

為了在實驗上直接觀測此類光學拓撲轉變，研究人員采用了掃描近場光學顯微鏡（s-SNOM）來表征氧化鉬的近場光學分布。如圖3所示，氧化鉬表面的金納米天線可以有效的聚焦紅外光，從而激發極化激元，其光學信號通過針尖散射收集到探測器。

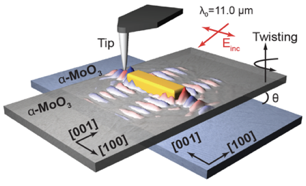
圖3 掃描近場光學顯微鏡示意圖。

金納米天線可以有效的激發極化激元，

當用針尖在氧化鉬表面逐點掃描后，

可以得到近場光學圖像。

從圖4中可以看到：

當雙層氧化鉬轉角為30度時，極化激元表現為傾斜的內陷型波前，說明等頻線為傾斜的開口雙曲線；

當轉角增大到54度時，極化激元只沿著一個方向傳播，說明其等頻線為平帶；

當轉角繼續增大到90度時，極化激元可以沿著所有面內方向傳播，說明其等頻線為閉合型。

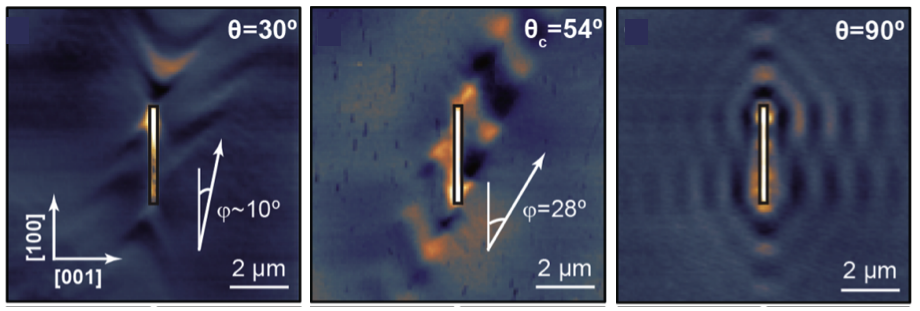
圖4 不同轉角雙層氧化鉬的近場光學圖像。

極化激元的傳播隨著轉角的不同發生很明顯的變化，

表明了光學拓撲轉變。

從實驗中看到，通過改變雙層氧化鉬之間的轉角，可以直觀的看到從開口到閉合的光學拓撲轉變，這與之前的理論研究一致。

需要強調的是這里的拓撲現象不同于拓撲光子學中陳數（名詞拓展）的變化，而是類比于Lifshitz轉變，即電子的能帶可以從雙曲線型（開口）變化到橢圓型（閉合），其性質會發生巨大的變化。

更加有趣的是，當等頻線為平帶時，極化激元只能沿一個方向傳播，并且沒有衍射，這是因為所有的Poynting矢量（名詞解釋）都沿著同一個方向。

如圖5所示，通過比較發現，當轉角為54度時，衡量衍射損耗的因子（f）為零，這與常見的極化激元有很大不同（f為0.5）。

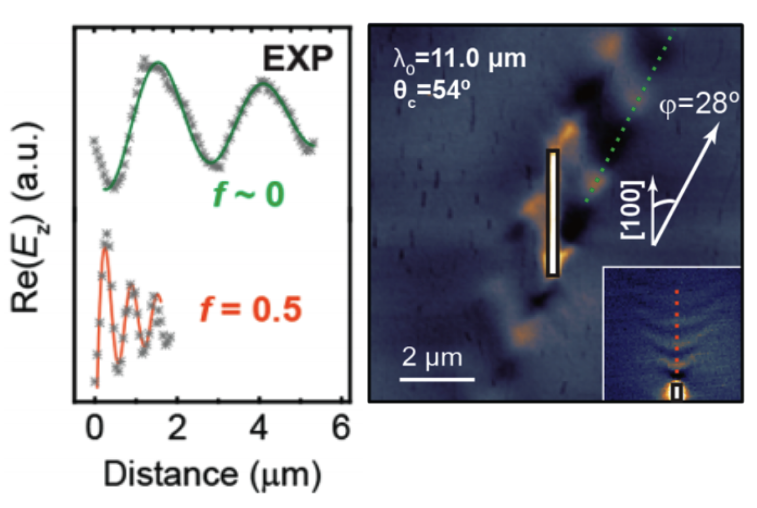
圖5 極化激元的無衍射傳播。

通過對比轉角氧化鉬和單層氧化鉬發現，

當轉角為54度時，

聲子極化激元可以沿固定方向無衍射傳播。

第二類光學拓撲轉變

除了第一類光學拓撲轉變外，我們還發現通過改變氧化鉬周圍的介電環境，可以實現第二類拓撲轉變，即雙曲線型的等頻線經歷閉合然后轉向的過程。

理論研究（圖6）表明，當氧化鉬在二氧化硅襯底時，極化激元表現為中心軸沿著［100］方向的雙曲線型等頻線。然而，當我們把氧化鉬放到碳化硅襯底時，極化激元表現為中心軸沿［001］方向的雙曲線等頻線，與二氧化硅襯底相比旋轉了90度。

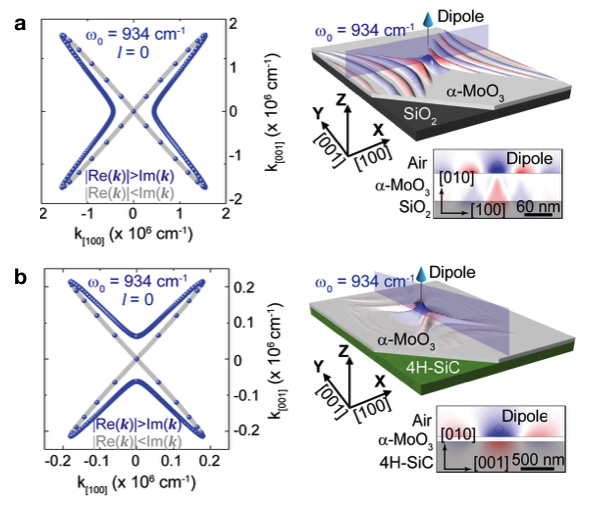
圖6 不同襯底下氧化鉬聲子極化激元的比較。

當襯底為二氧化硅時，

等頻線中心軸沿著［100］方向。

而當襯底為碳化硅時，

等頻線中心軸變為［001］方向。

這是由于在紅外波段，氧化硅的介電常數為正值，表現了一個常見的介質襯底，而碳化硅的介電常數為負值，存在表面聲子極化激元，這就導致了氧化鉬中極化激元和碳化硅極化激元的耦合，從而引起了體系內等頻線的變化。

同樣的，為了在實驗中觀測這一現象，我們采用s-SNOM獲得了氧化鉬在不同襯底下的近場光學圖像。如圖7所示，我們對比了二氧化硅和碳化硅襯底上氧化鉬的近場光學圖像，發現與理論預言一致：二氧化硅襯底上極化激元沿著［100］方向傳播，碳化硅襯底上沿著［001］方向傳播。這說明通過改變氧化鉬的介電環境，不僅可以起到調控極化激元波長的作用，還可以控制其傳播方向。

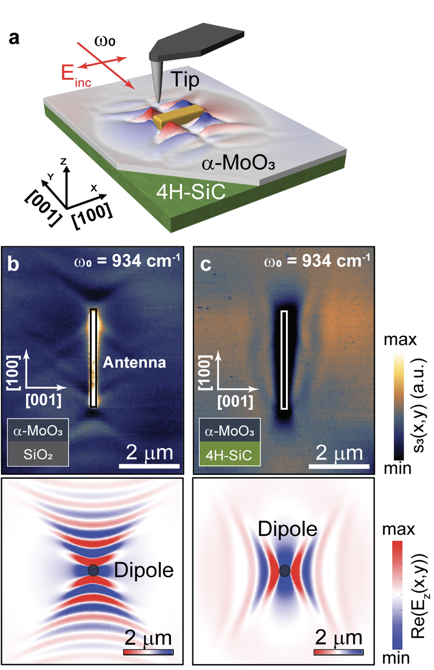
圖7 不同襯底上氧化鉬聲子極化激元的近場光學圖像。

a，掃描近場光學顯微鏡的示意圖。

b，二氧化硅上氧化鉬的近場光學圖像和數值模擬。

c，碳化硅上氧化鉬的近場光學圖像和數值模擬。

為了進一步研究極化激元等頻線旋轉中涉及到的拓撲轉變，我們改變入射光的頻率對碳化硅上的氧化鉬進行了近場光學表征（如圖8所示）。

當入射光頻率為948 cm-1時，極化激元沿著［100］方向傳播，即等頻線為中心軸沿著［100］方向的雙曲線，這與氧化硅襯底的情況類似；

當入射光頻率為937 cm-1時，極化激元變為沿著［001］方向傳播，即等頻線旋轉了90度。

當入射光頻率介于兩者之間（943 cm-1），我們觀測到了一種很奇特的等頻線，為兩條相交于一點的直線。

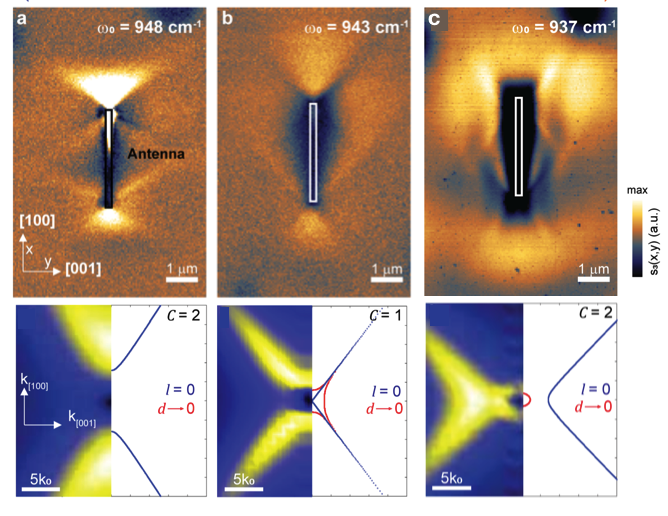
圖8 不同入射光頻率下極化激元的近場光學成像，

襯底為碳化硅。

當入射光頻率逐漸減小時，

極化激元等頻線經歷了第二類光學拓撲轉變。

這個實驗表明：隨著入射光頻率的減小，等頻線先為中心軸沿著［100］方向的雙曲線，然后變為相交于一點的兩條直線，最后變為中心軸沿著［001］的雙曲線，與第二類光學拓撲轉變一致（圖1）。

為了進一步研究此類光學拓撲轉變，我們從理論上計算了不同入射光頻率下極化激元等頻線的變化規律，如圖9所示。當入射光頻率為943cm-1時，雙曲線變為了兩條直線，并且相交于一點，直接證明了第二類拓撲轉變。

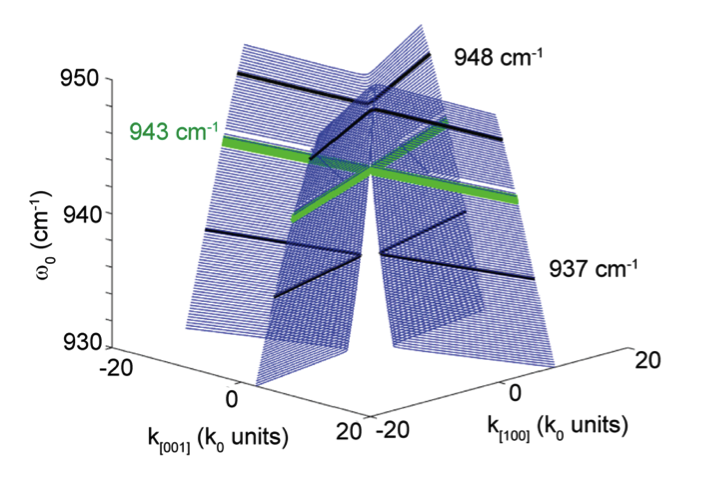
圖9 碳化硅上氧化鉬中極化激元等頻線的理論計算結果。

當入射光頻率為當入射光頻率為943cm-1時，

雙曲線變為了兩條直線，并且相交于一點（綠色實線）。

將拓撲學的概念引入納米光子學中有助于在納米尺度下對光與物質相互作用以及光子傳播的調控，也有助于從理論上理解光子的行為。

通過轉角來調控天然范德瓦爾斯晶體的光學色散奠定了“轉角光子學”的基礎，對光子的調控提供了一個全新的維度。可以想象，光學拓撲轉變帶來的新奇物理現象會對光學成像，光子集成以及量子光學產生重要的影響。
編輯：lyn