引言
本文講述霍夫變換的一些內容,并加入一些理解性東西,參考了部分博客等相關性內容。希望能對霍夫變換有所了解,也希望看到的人如果發現錯誤及時幫忙糾正。博主水平有限,還望賜教。
歷史和簡介
歷史
霍夫變換(Hough Transform)是在1959年由氣泡室(Bubble Chamber)照片的機器分析而發明,發明者Paul Hough在1962年獲得美國專利,被命名為Method and Means for Recognizing Complex Patterns(用于識別復雜圖案的方法和手段)。該專利對直線采用斜截距參數化,但由于斜率可能變成無窮大,這有可能導致無限變換空間(unbounded transform space)。
現在使用的霍夫變換是1972年由Richard Duda和Peter Hart所發明,稱為“廣義霍夫變換[GHT]”(Use of the Hough Transformation to Detect Lines and Curves in Pictures,1972)。
然后1981年在Dana H. Ballard的計算機視覺社區中出現一篇文章名為 Generalizing the Hough transform to detect arbitrary shapes,從而推廣開來。
該文描述了使用模板匹配原理對霍夫變換進行修改。要知道霍夫變換最初是為了分析定義的形狀(如線、圓、橢圓等)而開發。通過了解其形狀并旨在其找出圖像中的位置和方向,這種改變使得霍夫變換能夠檢測用其模型描述的任意對象。這將圖像中查找對象(用模型描述)的問題通過查找模型在圖像中的位置來解決。利用廣義霍夫變換(GHT),找到模型位置的問題轉換為尋找將模型映射到圖像中的變換參數的問題。給定變換參數的值,就可以確定模型在圖像中的位置。
后來產生了更多霍夫變換的變體和擴展,比如KHT,3DKHT,這里不細致說明。
簡介
霍夫變換是一個特征提取技術。其可用于隔離圖像中特定形狀的特征的技術,應用在圖像分析、計算機視覺和數字圖像處理領域。目的是通過投票程序在特定類型的形狀內找到對象的不完美實例。這個投票程序是在一個參數空間中進行的,在這個參數空間中,候選對象被當作所謂的累加器空間中的局部最大值來獲得,所述累加器空間由用于計算霍夫變換的算法明確地構建。最基本的霍夫變換是從黑白圖像中檢測直線(線段)。Hough變換主要優點是能容忍特征邊界描述中的間隙,并且相對不受圖像噪聲的影響。
原理
霍夫變換最簡單的是檢測直線。我們知道,直線的方程表示可以由斜率和截距表示(這種表示方法,稱為斜截式),如下所示:
如果用參數空間表示則為,即用斜率和截距就能表示一條直線。
但是這樣會參數問題,垂直線的斜率不存在(或無限大),這使得斜率參數的值接近于無限。為此,為了更好的計算,Richard O. Duda和Peter E. Hart在1971年4月,提出了Hesse normal form(Hesse法線式)
其中是原點到直線上最近點的距離(其他人可能把這記錄為,下面也可以把r看成參數),是軸與連接原點和最近點直線之間的夾角。如圖1所示。
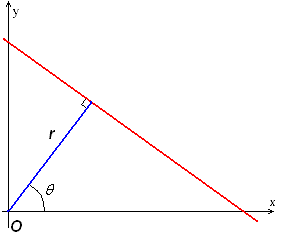
圖1
因此,可以將圖像的每一條直線與一對參數相關聯。這個參數平面有時被稱為霍夫空間,用于二維直線的集合。
在概念上,霍夫變換很接近Radon變換有人將之看成同一變換的不同形式
經過Hough變換,將圖像空間中的一個點映射到Hough空間,如圖2所示。
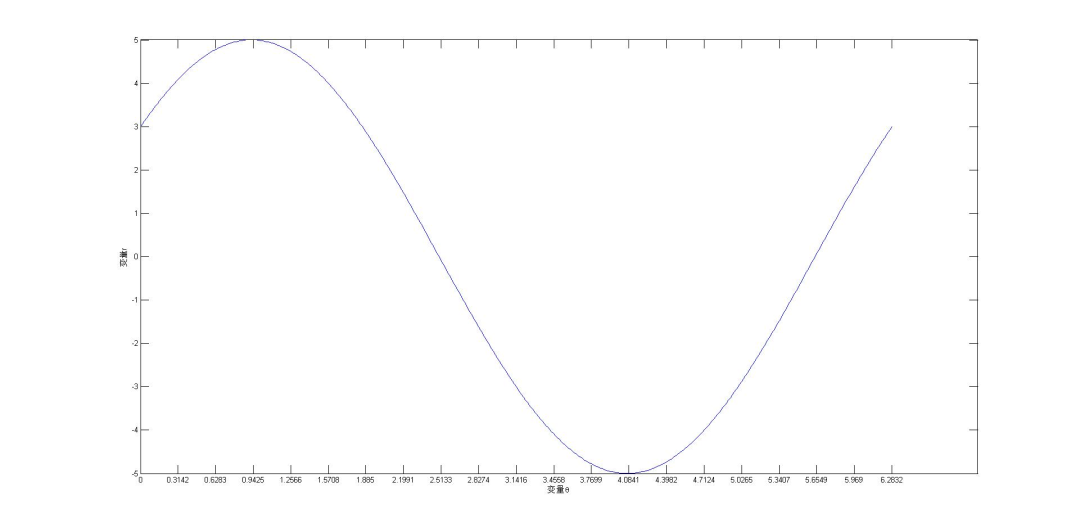
圖2
圖2:固定一個點(3,4),在角度取時,r的取值范圍情況. 該圖是用matlab繪制,代碼如下
% 一個點的坐標為(3,4)
x=3;
y=4;
%將給定的一個定點映射到霍夫變換空間
theta=0:pi/200:2*pi;% 角度
r=x*cos(theta)+y*sin(theta);
plot(theta,r);%繪圖
set(gca,‘XTick’,[0:pi/10:2*pi]); % 修改x軸坐標間隔
xlabel(‘變量 heta’)
ylabel(‘變量r’)繼續正題內容,圖2顯示了經過定點時的關系。顯示了在極坐標對極徑極角平面繪出所有通過該定點的直線, 將得到一條正弦曲線。正弦曲線的形狀取決于,點到所定義原點的距離。通常,越大,正弦曲線的振幅越大,反之則會越小。
所以我們可以得到一個結論,給定平面中的單個點,那么通過該點的所有直線的集合對應于平面中的正弦曲線,這對于該點是獨特的。一組兩個或更多點形成一條直線將產生在該線的處交叉的正弦曲線。因此,檢測共線點的問題可以轉化為找到并發曲線的問題。
例子1
考慮下面三個點,這里顯示為黑點
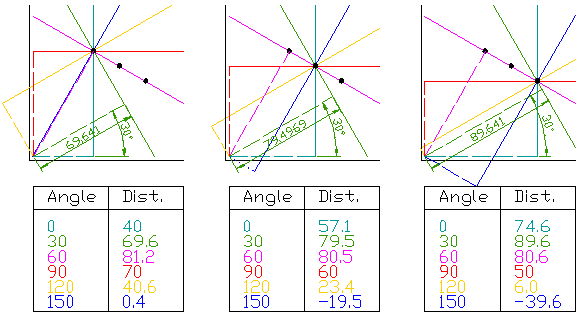
圖3
該圖顯示了Hough變換的第一步,三點和六個可能的角度分組。最左邊的圖像顯示正在轉換的第一個點。首先,繪制不同角度的線條,全部經過第一點。這些顯示為實線。其次,對于每條實線,找到也將原點平分的垂線(法線,或者說連接原點垂直于線段的線),這些顯示為虛線。然后找到虛線的長度和角度。這些值顯示在圖表下方的表格中。這對被轉換的三個點中的每一個都重復該過程。然后將結果繪制成圖,有時稱為霍夫空間圖。
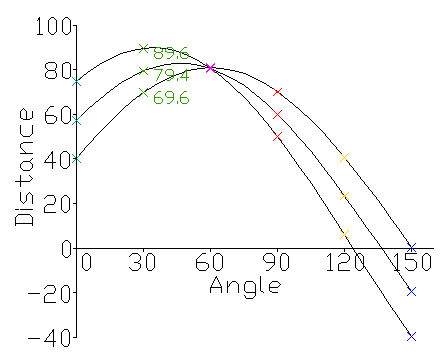
圖4
這顯示一個霍夫空間圖,三點和六個可能的角度。這是前面表格中數據的一個簡單圖表。線彼此交叉的點表示由作為變換輸入的三個點形成的線的角度和距離.
圖4顯示的曲線相交的點給出距離和角度。該距離和角度表示與被測試點相交的線。在圖4中,所示的線條在粉紅點相交; 這對應于圖3中的實線粉紅線,其穿過所有三個點。
在圖像分析上下文,邊緣段的點(一個或多個)的坐標在圖像中是已知的,并且因此作為參數線等式中的常量,而與是未知變量是我們要尋找的。如果我們繪制由每個定義的可能值,笛卡爾圖像空間中的點映射到極性霍夫參數空間中的曲線(即正弦曲線)。這個點到曲線的變換是直線的霍夫變換。當在霍夫參數空間中查看時,在笛卡爾圖像空間中共線的點變得很明顯,因為它們產生在相同點相交的曲線。
例子2
以下是顯示包含兩條粗線的光柵圖像上的霍夫變換結果的不同示例。
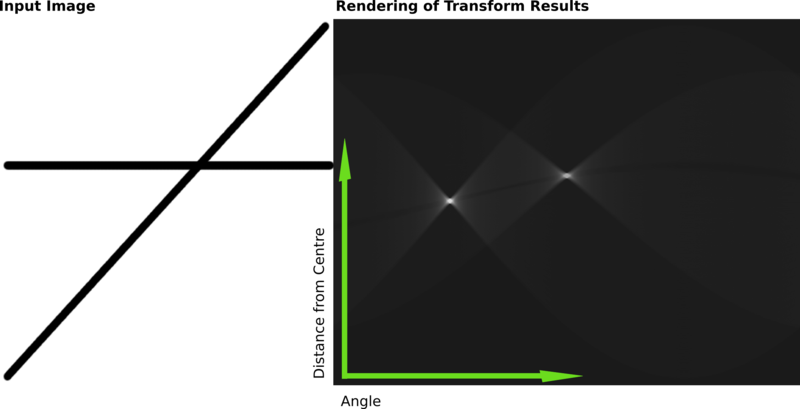
該變換的結果存儲在矩陣中。單元格值表示通過任意點的曲線數量。更高的單元格值變得更亮。兩個明顯的亮點是兩條線的霍夫參數。從這些點的位置,可以確定輸入圖像中兩條線的圖像中心的角度和距離。
霍夫變換提取直線如何實現?實現機理是為何???
通過將霍夫參數空間量化為有限間隔或累加器單元來實現變換。隨著算法的運行,每個算法都把轉換為一個離散化的曲線,并且沿著這條曲線的累加器單元被遞增。累加器陣列中產生的峰值表示圖像中存在相應的直線的有力證據。??注意,現在我們考慮的是直線的霍夫變換(先不去考慮圓,圓的情況稍后簡單說明)。累加器陣列的維度是二維的(也就是r和)。
用霍夫變換檢測圓時,累加器是三維累加器,目前不去論述
那么對于圖像來說,處的每個像素及其鄰域,霍夫變換算法被用于確定該像素是否有足夠的直線證據。如果是,它將計算該線的參數,然后查找參數落入的累加器箱,并增加該箱的值(投票值)。通過查找具有最高值的箱,通常通過查找累加器空間中的局部最大值,可以提取最可能的線,并且讀出它們的(近似的)幾何定義。
找到這些峰的最簡單方法是通過應用某種形式的閾值,但其他技術可能在不同情況下產生更好的結果 - 確定找到哪些行以及有多少。由于返回的行不包含任何長度信息,因此通常有必要在下一步中查找圖像的哪些部分與哪些行匹配。此外,由于邊緣檢測步驟中存在缺陷誤差,通常會在累加器空間中出現錯誤,這可能使得找到合適的峰值以及適當的線條變得非常重要。
線性霍夫變換的最終結果是類似于累加器的二維陣列(矩陣),該矩陣的一個維度是量化角度,另一個維度是量化距離r。矩陣的每個元素的值等于位于由量化參數表示的線上的點或像素的總和。所以具有最高值的元素表示輸入圖像中代表最多的直線。在某些論文中,可能把累計器單元的結果認為是投票值。換句話說,將每個交點看成一次投票,也就是說,所有點都如此進行計算后,可以設置一個閾值,投票大于這個閾值的可以認為是找到的直線。下圖是從一個博客摘用。

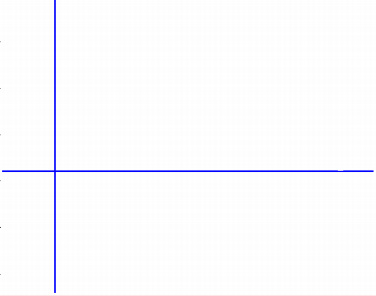
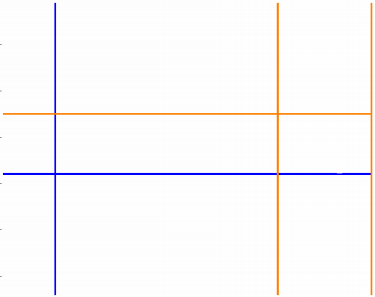
分別為原圖,閾值為30,20時候檢測到的直線。對于大于閾值的點,有其Hough space的參數對通過逆映射我們可以得到圖像空間中的直線:
實現使用的例子說明描述
霍夫變換可用于識別最適合一組給定邊緣點的曲線的參數。該邊緣描述通常從諸如Roberts Cross,Sobel或 Canny邊緣檢測器的特征檢測算子獲得,并且可能是嘈雜的,即其可能包含對應于單個整體特征的多個邊緣片段。此外,由于邊緣檢測器的輸出僅限定圖像中的特征的位置,所以霍夫變換進一步是確定兩個特征是什么(即檢測其具有參數(或其他)的特征描述)以及 它們有多少個存在于圖像中。
為了詳細說明霍夫變換,我們從兩個閉合矩形的簡單圖像開始。
簡單閉合矩形
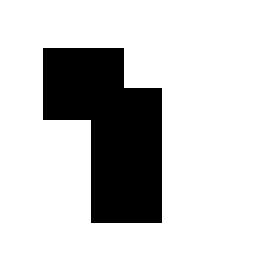
使用 Canny邊緣檢測器可產生一組邊界描述的這個部分,如圖8所示。
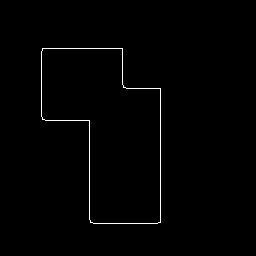
這里我們看到了圖像中的整體邊界,但是這個結果并沒有告訴我們這個邊界描述中的特征的身份(和數量)。在這種情況下,我們可以使用Hough(線檢測)變換來檢測該圖像的八個單獨的直線段,從而確定對象的真實幾何結構。
如果我們使用這些邊緣/邊界點作為Hough變換的輸入,則會在笛卡爾空間中的每個邊緣點的極坐標空間中生成一條曲線。當被視為強度圖像時,累加器陣列看起來像圖9所示

圖9
可以利用直方圖 均衡技術使得圖像可以讓我們看到包含在低強度像素值中的信息模式,如圖10所示。

注意,雖然和是概念上的極坐標,但是累加器空間以橫坐標和縱坐標的矩形繪制 。請注意,累加器空間環繞圖像的垂直邊緣,因此實際上只有8個實際峰值。
由梯度圖像中的共線點生成的曲線在霍夫變換空間中的峰中相交。這些交點表征原始圖像的直線段。有許多方法可用于從累加器陣列中提取這些亮點或局部最大值。例如,一個簡單的方法涉及閾值處理,然后 對累加器陣列圖像中孤立的亮點集群進行一些細化處理。這里我們使用相對閾值來提取,對應于原始圖像中的每條直線邊緣的點。(換句話說,我們只采用累加器數組中的那些局部最大值,其值等于或大于全局最大值的某個固定百分比。)
從Hough變換空間(即,反霍夫變換)映射回笛卡爾空間產生一組圖像主題的線描述。通過將該圖像疊加在原始的反轉版本上,我們可以確認霍夫變換找到兩個矩形的8個真實邊的結果,并且因此揭示了遮擋場景的基礎幾何形狀。
從Hough變換空間(即,反霍夫變換)映射回笛卡爾空間產生一組圖像主題的線描述。通過將該圖像疊加在原始的反轉版本上(見圖11),我們可以確認霍夫變換找到兩個矩形的8個真實邊的結果,并且因此揭示了遮擋場景的基礎幾何形狀。
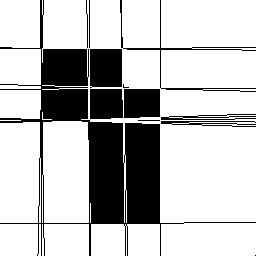
圖11
請注意,在這個簡單的例子中,檢測到的和原始圖像線的對齊精度顯然不完美,這取決于累加器陣列的量化。(還要注意許多圖像邊緣有幾條檢測線,這是因為有幾個附近的霍夫空間峰值具有相似的線參數值,存在控制這種效應的技術,但這里沒有用來說明標準霍夫變換。)
還要注意,由霍夫變換產生的線條的長度是無限的。如果我們希望識別產生變換參數的實際線段,則需要進一步的圖像分析以便查看這些無限長線的哪些部分實際上具有點。
為了說明Hough技術對噪聲的魯棒性,Canny邊緣描述已被破壞(由椒鹽噪聲引起), 在Hough變換之前,如圖12所示。

圖12
繪制在霍夫空間的結果如圖13所示。

圖13
將這個結果反霍夫變換(并將它覆蓋在原來的結果上,見圖14)
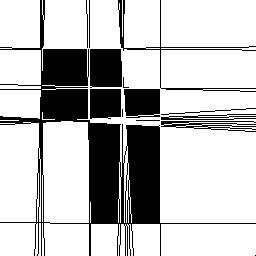
圖14
圖14:相對閾值設置為40%。
可以通過變換圖像來研究Hough變換對特征邊界中的間隙的敏感性(使用了畫圖工具進行編輯,見圖15)
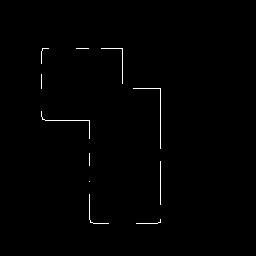
圖15
然后我們再將其變換到霍夫變換空間,表示為圖16所示。

圖16
然后使用40%的相對閾值去對圖像反霍夫變換(同樣也是疊加在原圖上
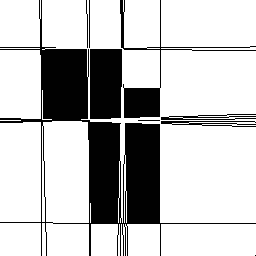
圖17
在這種情況下,因為累加器空間沒有接收到前面例子中的條目數量,只能找到7個峰值,但這些都是結構相關的線。
前面的例子都不是自然實例。下面展示自然實例的例子。
城市場景
在第一種情況下,我們有一個城市場景,這些建筑物被霧遮住,見圖18。

圖18
如果我們想要找到建筑物的真實邊緣,邊緣檢測器(例如Canny)無法很好地恢復這些信息,如圖19所示。

圖19
但是,霍夫變換可以檢測到一些表示遮擋區域內建筑物邊緣的直線。原始圖像的直方圖均衡累加器空間表示如圖20所示。

圖20
如果我們將相對閾值設置為70%,我們會得到如圖21所示的反霍夫變換圖像。

圖21
這里只能檢測到幾條長邊,并且在很多線條或邊緣片段幾乎共線的地方存在很多重復。應用更大的相對閾值(即50%)會產生如圖22所示效果。

圖22
會產生更多的預期線條,但會以許多共線邊緣碎片產生的許多虛假線條為代價。
最后一個例子來自遙感應用。在這里,我們想要檢測圖像中的街道
遙感應用

圖23
圖23顯示了一個合理的矩形城市扇區(rectangular city sector)。我們可以使用Canny邊緣檢測器來檢測該圖像,如圖24所示。

圖24
但是,街道信息不能單獨用作邊緣檢測器的輸出。
圖25表明霍夫線檢測器能夠恢復這些信息中的一些。但由于原始圖像的對比度較差,因此確定了一組有限的特征(即街道)。

圖25
實現算法描述
摘取一篇博客的算法描述:
初始化空間,表示在該參數表示的直線上的像素點的個數)
對于每一個像素點,在參數空間中找出滿足的對,然后令
統計所有的大小,取出的參數 (τ是預設的閾值)
但我覺得這并不是十分完整的算法流程。所以我將其改進描述如下
讀取原始圖并轉換成灰度圖,采用邊緣檢測算子(如Canny)轉換成二值化邊緣圖像
然后對該圖像進行霍夫變換
先使用峰值檢測函數,找到大于閾值的霍夫變換單元(局部最大值應該最可能是線,步長和量化會影響效果)
將上述識別出的一組候選峰,需要確定與其相關的線段及其起始點和終止點(這需要一定的算法,很多論文對此都做了改進,諸如蝴蝶形狀寬度,峰值走廊)
然后描繪于原圖(或結果圖)上
代碼實現
matlab版本
原圖

圖26
%讀取圖像
I = imread(‘huofu.jpg’);
% 轉換成灰度圖
grayI = rgb2gray(I);
% 創建二進制圖像
BW = edge(grayI,‘canny’);
% 使用二值圖像創建Hough變換。
[H,T,R] = hough(BW);
imshow(H,[],‘XData’,T,‘YData’,R,。。。
‘InitialMagnification’,‘fit’);
xlabel(‘ heta’), ylabel(‘
ho’);
axis on, axis normal, hold on;
% 在圖像的霍夫變換中查找峰值
P = houghpeaks(H,5,‘threshold’,ceil(0.3*max(H(:))));
x = T(P(:,2)); y = R(P(:,1));
plot(x,y,‘s’,‘color’,‘white’);
% 找到線條并繪制它們
lines = houghlines(BW,T,R,P,‘FillGap’,5,‘MinLength’,7);
figure, imshow(I), hold on
max_len = 0;
for k = 1:length(lines)
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),‘LineWidth’,2,‘Color’,‘green’);
% 繪制線條的開始和結束
plot(xy(1,1),xy(1,2),‘x’,‘LineWidth’,2,‘Color’,‘yellow’);
plot(xy(2,1),xy(2,2),‘x’,‘LineWidth’,2,‘Color’,‘red’);
% 確定最長線段的端點
len = norm(lines(k).point1 - lines(k).point2);
if ( len 》 max_len)
max_len = len;
xy_long = xy;
end
end
% 通過為青色著色來突出顯示最長的線段
plot(xy_long(:,1),xy_long(:,2),‘LineWidth’,2,‘Color’,‘cyan’);
運行結果
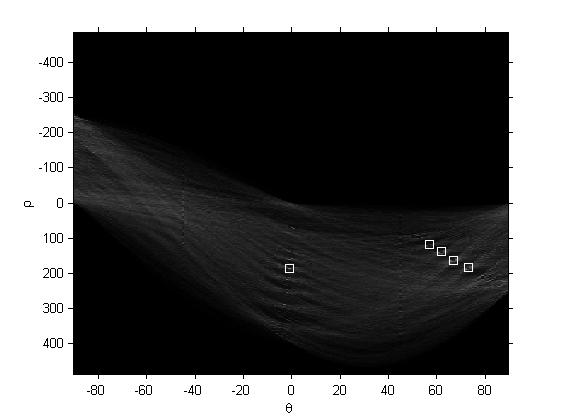

圖27
只是個示范使用,參數可自調。
python實現
#! python2
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import hough_line
from skimage.draw import line
img = np.zeros((100, 150), dtype=bool)
img[30, :] = 1
img[:, 65] = 1
img[35:45, 35:50] = 1
rr, cc = line(60, 130, 80, 10)
img[rr, cc] = 1
img += np.random.random(img.shape) 》 0.95
out, angles, d = hough_line(img)
fix, axes = plt.subplots(1, 2, figsize=(7, 4))
axes[0].imshow(img, cmap=plt.cm.gray)
axes[0].set_title(‘Input image’)
axes[1].imshow(
out, cmap=plt.cm.bone,
extent=(np.rad2deg(angles[-1]), np.rad2deg(angles[0]), d[-1], d[0]))
axes[1].set_title(‘Hough transform’)
axes[1].set_xlabel(‘Angle (degree)’)
axes[1].set_ylabel(‘Distance (pixel)’)
plt.tight_layout()
plt.show()
運行結果
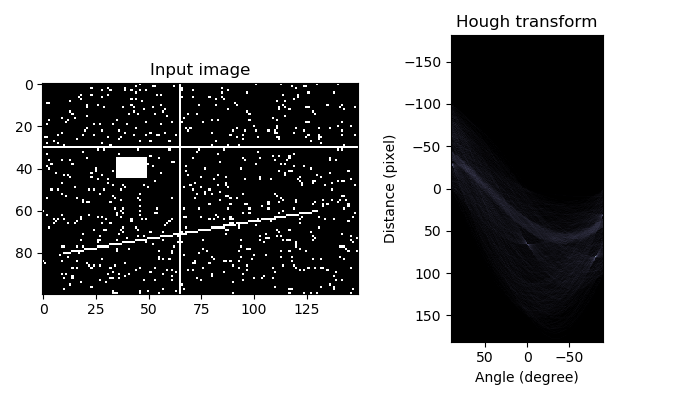
圖28
Opencv實現
opencv的關于霍夫變換提取的函數可以在Opencv的該文檔見到 Opencv關于houghlines函數 ??博主電腦安裝的是opencv2.4.13版本,代碼是來自于淺墨大神(毛星云)的代碼實現。
//-----------------------------------【頭文件包含部分】---------------------------------------
// 描述:包含程序所依賴的頭文件
//----------------------------------------------------------------------------------------------
#include 《opencv2/opencv.hpp》
#include 《opencv2/imgproc/imgproc.hpp》
//-----------------------------------【命名空間聲明部分】---------------------------------------
// 描述:包含程序所使用的命名空間
//-----------------------------------------------------------------------------------------------
using namespace cv;
//-----------------------------------【main( )函數】--------------------------------------------
// 描述:控制臺應用程序的入口函數,我們的程序從這里開始
//-----------------------------------------------------------------------------------------------
int main()
{
//【1】載入原始圖和Mat變量定義
Mat srcImage = imread(“1.jpg”); //工程目錄下應該有一張名為1.jpg的素材圖
Mat midImage, dstImage;//臨時變量和目標圖的定義
//【2】進行邊緣檢測和轉化為灰度圖
Canny(srcImage, midImage, 50, 200, 3);//進行一此canny邊緣檢測
cvtColor(midImage, dstImage, CV_GRAY2BGR);//轉化邊緣檢測后的圖為灰度圖
//【3】進行霍夫線變換
vector《Vec2f》 lines;//定義一個矢量結構lines用于存放得到的線段矢量集合
HoughLines(midImage, lines, 1, CV_PI / 180, 150, 0, 0);
//【4】依次在圖中繪制出每條線段
for (size_t i = 0; i 《 lines.size(); i++)
{
float rho = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * (a));
pt2.x = cvRound(x0 - 1000 * (-b));
pt2.y = cvRound(y0 - 1000 * (a));
line(dstImage, pt1, pt2, Scalar(55, 100, 195), 1, CV_AA);
}
//【5】顯示原始圖
imshow(“【原始圖】”, srcImage);
//【6】邊緣檢測后的圖
imshow(“【邊緣檢測后的圖】”, midImage);
//【7】顯示效果圖
imshow(“【效果圖】”, dstImage);
waitKey(0);
return 0;
}
運行結果

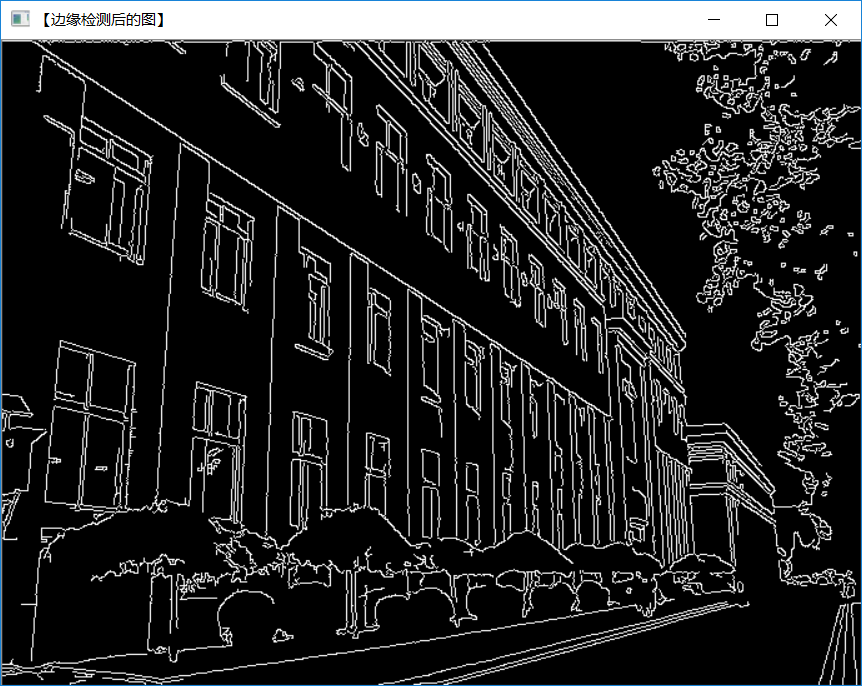
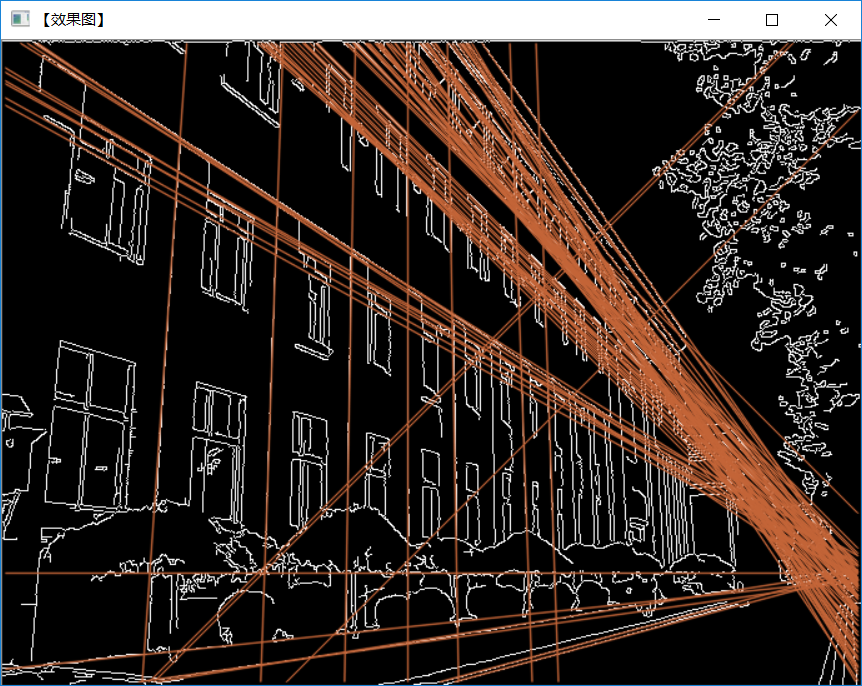
圖30
淺提霍夫變換提取圓
我們可以使用這個相同的程序來檢測具有分析描述的其他特征。例如,在圓圈的情況下,參數方程為
其中a和b是圓心的坐標并且是半徑。在這種情況下,算法的計算復雜度開始增加,因為我們現在在參數空間和三維累加器中有三個坐標。(通常,累加器陣列的計算和大小隨著參數數量的增加而多項式增加,因此,基本霍夫技術僅適用于簡單曲線。)
步驟
它的算法步驟如下:
首先創建累加器空間,由每個像素單元格構成。最初每個單元格都設置為0。
然后對于每個圖像中的邊緣點,按照圓方程將那些可能是一個圓中心的單元格值進行累加。這些單元格在等式中由字母a表示。
然后在前面的步驟中由每個可能找到的值a,區找到滿足等式的所有可能值b
搜索累加器空間中的局部最大值。這些單元格表示算法檢測到的圓圈。?? 如果我們不知道事先定位的圓的半徑,可以使用三維累加器空間來搜索具有任意半徑的圓。當然,這在計算上更加昂貴。
該方法還可以檢測部分位于累加器空間外部的圓,只要該圓的區域內仍有足夠的圓。
霍夫變換提取圓的一些實現鏈接
-matlab關于霍夫變換提取圓
Matlab圓提取(https://ww2.mathworks.cn/help/images/ref/imfindcircles.html)
-關于opencv的提取圓(給出了C++,C和Python)
Opencv官方文檔關于圓提取(https://docs.opencv.org/2.4/modules/imgproc/doc/feature_detection.html?highlight=HoughCircles)
- python實現提取圓
Python圓提取(https://scikit-image.org/docs/dev/api/skimage.transform.html)
淺提廣義霍夫變換
當我們希望隔離的特征的形狀不具有描述其邊界的簡單解析方程時,使用廣義Hough變換。在這種情況下,我們不使用曲線的參數方程,而是使用查找表來定義邊界位置和方向與霍夫參數之間的關系。(必須使用原型形狀在初步階段計算查找表值。)
例如,假設我們知道所需特征的形狀和方向。(見下圖)我們可以在特征中指定一個任意參考點,其中定義了特征的形狀(即r從邊界到這個參考點的法線的距離和角度ω。我們的查找表(即 R表)將由這些距離和方向對組成,由邊界的方向ω索引
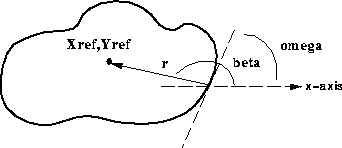
圖31
圖31:R表組件的描述。
霍夫變換空間現在是根據圖像中形狀的可能位置來定義的,即可能的范圍。換句話說,轉換定義為:
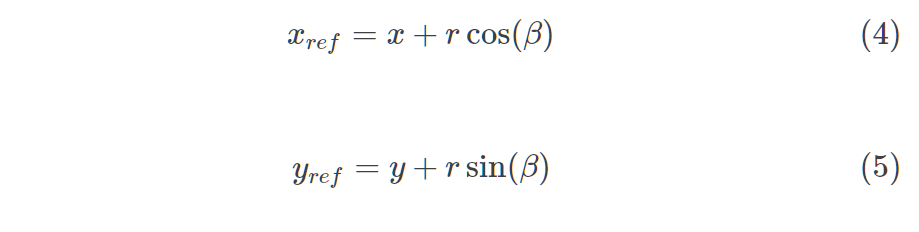
(對于特定的已知方向,β值和來自于表值)。如果所需特征的方向未知,則該過程變得復雜,因為我們必須通過引入額外參數來擴展累加器,以考慮方向。
基本霍夫變換的限制
霍夫變換只有在大量投票落入正確的分箱時才有效,因此可以在背景噪音中輕松檢測分箱。這意味著垃圾箱不能太小,否則有些選票會落入鄰近垃圾箱,從而降低主垃圾箱的可見度。
另外,當參數數量很大時(也就是說,當我們使用通常超過三個參數的霍夫變換時),單個分箱中投的平均投票數非常低,而這些分箱對應的實際數字在圖像中的投票數量并不一定比其鄰居多得多。復雜性以一定的速率增加,其中每個附加參數是圖像空間的大小和m是參數的數量。因此,必須非常小心地使用Hough變換來檢測線條或圓圈以外的任何其他內容。
最后,霍夫變換的大部分效率取決于輸入數據的質量:為了使霍夫變換高效,必須檢測邊緣。在噪聲圖像上使用Hough變換是一個非常棘手的問題,一般而言,之前必須使用降噪階段。在圖像被斑點破壞的情況下(如雷達圖像中的情況),Radon變換有時更適合檢測線,因為它通過求和來衰減噪聲。
結語
本博文主要描述基本經典的霍夫變換,描述了霍夫變換如何提取直線及其原理,展示了部分例子和代碼實現,也擴展了一部分霍夫變換的簡單描述,希望能對看者有所借鑒。
編輯:jq
-
光柵
+關注
關注
0文章
290瀏覽量
27559 -
邊緣檢測
+關注
關注
0文章
92瀏覽量
18229 -
累加器
+關注
關注
0文章
50瀏覽量
9475
原文標題:一文解讀經典霍夫變換(Hough Transform)
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
福田卡文汽車新能源技術戰略解讀
經典傅里葉變換與快速傅里葉變換的區別
歐姆定律和基爾霍夫定律的區別
博威合金攜手貝肯霍夫(中國)亮相埃森焊接展,打造焊材定制化解決方案





 一文解讀經典霍夫變換(Hough Transform)
一文解讀經典霍夫變換(Hough Transform)










評論